16.4 Refraction

Figure 16.10 As a marching band moves from a concrete parking lot to a grassy playing field, there may be changes in the length of the stride of the players, the speed of the band, and the direction of the band.

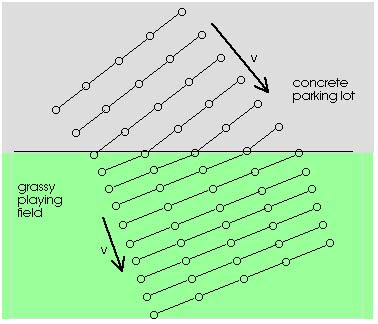
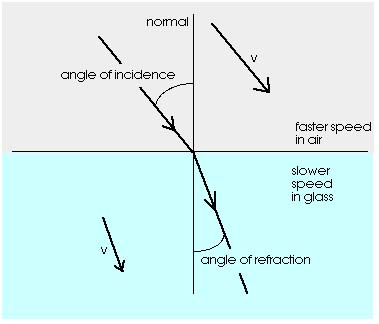
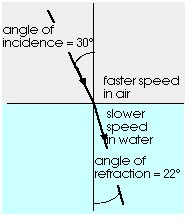
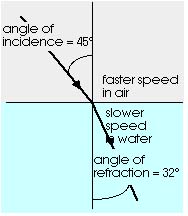
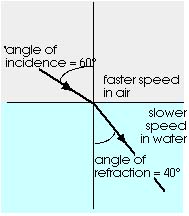
Figure 16.11 shows a ray of light moving from air into glass. The speed of light is greater in air than in glass, just as the speed of the band was greater on concrete than on grass. Light is bent as it goes from air to glass. Just as with the marching band, the light is bent toward the normal (the direction perpendicular to the surface). The direction of the incoming ray of light is given by the angle of incidence, the angle between the incoming ray and the normal (or perpendicular) to the surface. Light is bent as it goes from one material to another and this bending is called refraction. After the light enters the new material its direction is given by the angle of refraction, the angle between the outgoing ray and the normal (or perpendicular) to the surface. The angle of refraction depends upon the angle of incidence and the speed of light in the new material.

Figure 16.11 As light travels from air to glass, it is bent toward the normal (the line perpendicular to the surface).

Figure 16.12 shows the angles involved for different angles of incidence as light travels from air into water. Notice that when light strikes the surface head-on with an angle of incidence of 0¡, the angle of refraction is also 0¡. We should expect that from the symmetry of the situation.

Figure 16.12 As light goes from air into water, it is bent toward the normal (or perpendicular) due to the difference is the speed of light in air and in water.

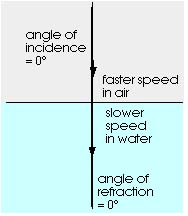
The speed of light is

c = 300,000 km/s

c = 3 x 10⁸ m/s

only in a vacuum. It is nearly that in air. But in other materials-like water or glass or plastic-it is considerably less than that. Instead of talking directly about the speed of light in such materials, we usually describe this speed in terms of the index of refraction which is the ratio of the speed of light in vacuum, c, to the speed of light in the material we are talking about, v. We label the index of refraction n and then can write

(Need Screen Capture)

Notice that the index of refraction does not carry any units since it is the ratio of one speed divided by another speed. Table 16.1 lists the speed of light and the index of refraction for several materials¹.

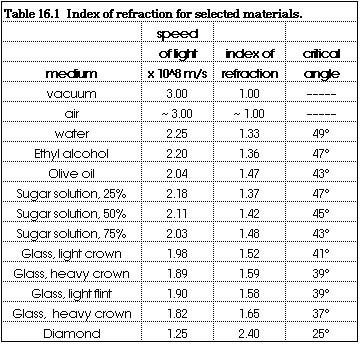
Q: If light travels from water into glass, will it be bent toward or away from the normal?

A: The index of refraction for water is 1.33 and the index of refraction of glass is about 1.55 so the index of refraction of water is less than the index of refraction of glass. This is the same situation we had in the examples in this section of light passing from air into water.

(need screen capture)

[Prev Section] [Next Section]

[Table of Contents] [Chapter Contents]