16.5 Total Internal Reflection

Figure 16.13 As light goes from water into air, it is bent away from the normal (or perpendicular) due to the difference is the speed of light in air and in water.

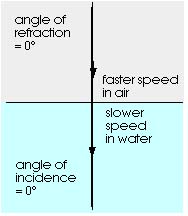
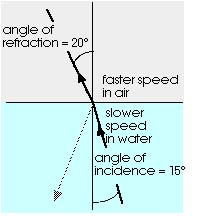
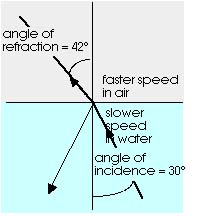
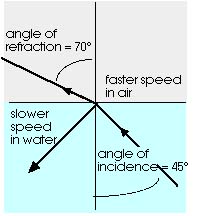
As light goes from water into air or from glass into air or from plastic into air, the light is bent away from the normal (or perpendicular). This happens when light goes from a material where its speed is slow into a material where its speed is fast. Bending away from the normal (or perpendicular) means the angle of refraction is greater than the angle of incidence for these cases. In addition to the refracted ray, there is also some light reflected at the surface. The amount of light reflected increases as the angle of refraction increases.

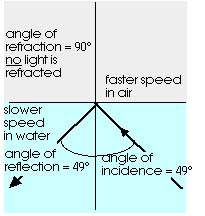
For some angle of incidence, the angle of refraction-the angle of the outgoing light-would be 90 meaning that all of the light that passes through into the air would be grazing across the surface. For that and all larger angles of incidence, no light will be transmitted into the air. All the light will be reflected at the water-air surface. This is known as total internal reflection. The smallest angle of incidence for which this happens is known as the critical angle. A list of critical angles for various materials is given in Table 16.1. Figure 16.14 illustrates this for a water-air surface where the critical angle is 49.

Figure 16.14 As light goes from water (n = 1.33) into air (n = 1.00), for angles of incidence greater than 49, no light will be refracted into the air. All the light will be reflected; this is known as total internal reflection. This angle of incidence is known as the critical angle.

Fig 16.E For reflections from water to air at angles greater than the critical angle, all the light is reflected. This is total internal reflection.

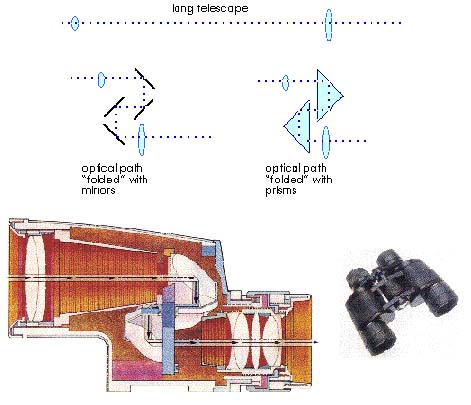
The critical angle depends upon the index of refraction. From Table 16.1 you can see that diamond has a very large index of refraction and the critical angle for diamond is relatively small. This means light will bounce around inside a diamond more often than with glass. Total internal reflection is important in the design of small, hand-held binoculars. Figure 16.15 illustrates a long telescope-a "spyglass" that you might see used in a swashbuckling pirate movie. Such a telescope is long and clumsy and difficult to handle. "Folding" the path of the light between the two lenses will make the device shorter and easier to handle. Mirrors could be used to reflect the light back and forth and accomplish this. However, mirrors absorb five to ten percent of the light they reflect. When you look at yourself in a bathroom mirror this does not make any difference. But when four reflections are involved and the image may be dim to begin with, loss of so much light is quite important. Instead of mirrors, we can arrange prisms so the light is reflected by total internal reflection. And total internal reflection really is that-it is total; there is no loss of light. Binoculars use such an arrangement of prisms as illustrated in Figure 16.15.

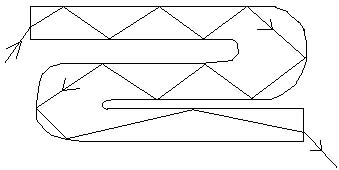
Figure 16.15 Reflections can make a set of binoculars much easier to handle than a long telescope. Reflections from mirrors reduce the amount of light. Total internal reflection, using prisms, keeps the image bright.

Total internal reflection is important in fiber optics that are now used for telephone communications-and for computers and television and other forms of communications. Figure 16.16 illustrates a light beam entering a fiber of glass or plastic. Even though the optic fiber may bend around curves and corners, the light will be reflected inside the optic fiber because the angles of reflection will be greater than the critical angle. Since these reflections are all by total internal reflection, there will be no light lost.

Figure 16.16 Fiber optics can carry light around corners or through a winding path.

Figure 16.17 Fiber optics now carry much of our telephone and other communications.

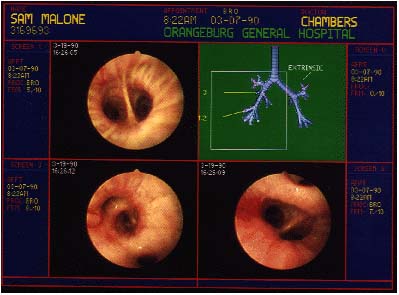
Total internal reflection is also important in fiber optics that are now literally revolutionizing internal medicine. Orthoscopic endoscopes allow an orthopedic surgeon to look behind a knee cap with a very small incision instead of major surgery. Other endoscopes allow all sorts of internal investigations without invasive surgery.

Figure 16.18 Total internal reflection allows information from one end of these endoscopes to be observed by a doctor at the other end. Such non-invasive medical tools are revolutionizing surgery.

Figure 16.F Endoscopes let physicians look inside our bodies without the trauma of invasive surgery.

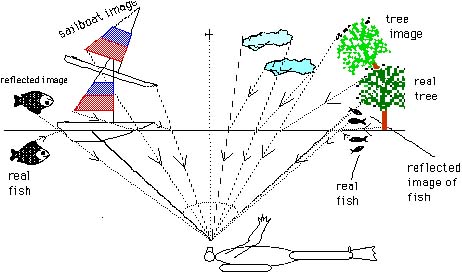
It is fun to describe what a scuba diver or a fish might see while underwater and looking up at a very smooth surface between the water and air. The light from the air above will be refracted so objects will appear to be somewhere other than where they "really" are. The light from some underwater objects will be reflected at the surface by total internal reflection-just as if the surface were a mirror-and mirror-images of them will appear above the water! Remember, we see something only by the light that actually reaches our eyes and then our eyes interpret that light assuming it has come along a straight path. Such a scuba diver is sketched in Figure 16.19. The figure looks rather messy-and there is a lot going on there-but let's look at the various pieces.

There is a bird flying directly above the scuba diver; light from the bird strikes the surface normal to the surface (incidence = 0) so it passes directly through without being bent. Light from the bottom of the tree just skims the water's surface. When it finally is bent, its angle of refraction is the critical angle, 49. The two heavier lines, in fact, mark the critical angle on either side of the normal. Light from the top of the tree is bent or refracted. The scuba diver sees these rays of light after they have been refracted. So he then "sees" the tree-the image of the tree, if you like-tilted and raised up toward the center of his vision. Likewise, the cloud and sailboat are distorted; their images are moved toward the normal. Everything above the water's surface is seen inside a circle whose half-angle is the critical angle (49 for air and water). Nothing that is seen outside this circle originated above the water. But the view is not black or void out there. Objects below the surface have their images reflected in the surface as a mirror and appear there. This is illustrated on both sides by the fish there.

Figure 16.19 A scuba diver has an interesting view of the airborne world when viewed from underwater (the surface must be very smooth to see this).

Q: If light travels from glass into ethyl alcohol, will it be bent toward or away from the normal?

A: The index of refraction for glass is about 1.55 and the index of refraction for ethyl alcohol is 1.36. In going from a material of higher index of refraction into a material of lower index of refraction, light is bent away from the normal.

Q: If light travels from olive oil into air can the light undergo total internal reflection?

A: Total internal reflection can occur if the first index of refraction is greater than the second. Olive oil has an index of refraction of 1.47 which is greater than air's index of refraction of 1.0. Therefore, total internal reflection may occur.

[Prev Section] [Next Section]

[Table of Contents] [Chapter Contents]