Ch 11, Rolling Motion
Homework: Ch11; 11, 14, 19, 30, 34, 54
Questions 1, 2, 3, 4, 10, 12, 13, 15
| Hmwk, Ch 10 | Homework Assignments | PHY 1350's Home | Hmwk, Ch 12 |
Additional problems from Serway's fourth edition
(4ed) 11.* A solid sphere has a radius of 0.200 m and a mass of 150 kg. How much work is required to get the sphere rolling with an angular speed of 50.0 rad/s on a horizontal surface? Assume the sphere starts from rest and rolls without slipping.
(4ed) 11.* Verify Equation 11.14 and show that the cross product may be written as
Problems from the current (5th) edition of Serway and Beichner.
11.11 Two vectors are given by A = - 3i + 4j and B = 2 i + 3 j.
Find (a) A x B
and (b) the angle between A and B.
A x B = i (Ay Bz - Az By) + j (Az Bx - Ax Bz) + k (Ax By - Ay Bx)
A x B = i (4 0 - 0 3) + j (0 2 - ( - 3) 0) + k ((-3) 3 - 4 2)
A x B = i (0 ) + j (0) + k (- 17) = - 17 k
We can also write this cross-product as
| A x B | = A B sin
A = |A| = SQRT [ ( - 3 )2 + ( 4 )2 + ( 0 )2 ] = SQRT [ 9 + 16 ] =
A = SQRT[ 25 ] = 5
B = |B| = SQRT [ 22 + 32 + 02 ] = SQRT [13]
| A x B | = 17
sin
= | A x B | / (A B) = 17 / [(5) SQRT(13)] = 17 / [(5)(3.61)] = 0.943
11.14 A student claims to have found a vector A such that (2 i - 3 j + 4 k) x A = 4 i + 3 j - k. Do you belive this claim? Explain.
We will need the cross-product in the form of Equation 11.14,
D x E = (Dx i + Dy j + Dz k) x (Ex i + Ey j + Ez k)
= i (Dy Ez - Dz Ey) + j (Dz Ex - Dx Ez) + k (Dx Ey - Dy Ez)
(I intentionally avoidedwriting A x B since this question already has an expression involving something like C x A, with vector A being the second or last vector in the expression. Now we can go ahead and evaluate (2 i - 3 j + 4 k) x A ,
(2 i - 3 j + 4 k) x A = (2 i - 3 j + 4 k) x (Ax i + Ay j + Az k)
= i [ ( - 3) Az - 4 Ay ] + j [ 4 Ax - 2 Az ] + k [ 2 Ay - ( - 3) Ax ]
= 4 i + 3 j - k
This gives three equations for the three components of vector A,
i [ ( - 3) Az - 4 Ay ] + j [ 4 Ax - 2 Az ] + k [ 2 Ay - ( - 3) Ax ] = 4 i + 3 j - k
- 3 Az - 4 Ay = 4
4 Ax - 2 Az = 3
2 Ay + 3 Ax = - 1
Now we just slog through the mire of simultaneous equations,
3 Az + 4 Ay = - 4
3 Az = - 4 Ay - 4
Az = ( - 4 Ay - 4 ) / 3
4 Ax - 2 Az = 3
4 Ax - 2 [ ( - 4 Ay - 4 ) / 3 ] = 3
4 Ax + 8 Ay / 3 + 8 / 3 = 3
12 Ax + 8 Ay + 8 = 9
12 Ax + 8 Ay = 1
2 Ay + 3 Ax = - 1
Multiply this latest equation by 4
12 Ax + 8 Ay = - 4
Now subtract this from 12 Ax + 8 Ay = 1
And we are in "trouble" for this results in
0 = 4
What does this mean? There is not a solution to our set of three simultaneous equations. So the vector A does not exist! How can this be? What does this mean?
In general, if we write B x A = V, this resulting vector V is perpendicular to both B and A. In our case, that requires that vector ( 4 i + 3 j - k ) be perpendicular to ( 2 i - 3 j + 4 k). Is that the case? Let's check it and see. If these two vectors were perpendicular, then their dot product should vanish.
Remember that
A
B = A B cos
and that
A
( 4 i + 3 j - k )
= 4
and that is not zero.
11.19 A light rigid rod 1.00 m in length rotates in the xy plane about a pivot through the rod's center. Two particles of masses 4.00 kg and 3.00 kg are connected to its ends. Determine the angular momentum of the system about the origin at the time the speed of each particle is 5.00 m/s.
LTot = Lrod + L1 + L2
We are told the rod is a "lightweight" rod, which is another way of saying its mass and its moment of inertia are small enough they may be ignored. Therefore,
LTot = L1 + L2
The angular momentum for a "point particle" is
L = m r vt
L1 = (3.0 kg) (0.5 m) (5.0 m/s) = 7.5 kg m2/s
L2 = (4.0 kg) (0.5 m) (5.0 m/s) = 10.0 kg m2/s
LTot = L1 + L2 = 17.5 kg m2/s
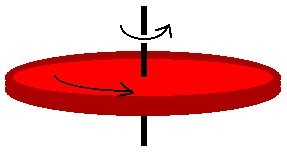
11.30 A uniform solid disk of mass 3.00 kg and radius 0.200 m rotates about a fixed axis perpendicular to its face. If the angular frequency of rotation is 6.00 rad/s, calculate the angular momentum of the disk when the axis of rotation
(a) passes through its center of mass and
(b) passes through a point midway between the center and the rim.
ICM = (1/2) M R2
ICM = (1/2) (3.00 kg) (0.200 m)2
ICM = 0.06 kg m2
L = I
= ( 0.06 kg m2) (6.0 1/s)
L = 0.54 kg m2 / s
I = ICM + M d2
I = (1/2) M R2 + M (R/2)2
I = (1/2) M R2 + (1/4) M R2
I = (0.06 + 0.03) kg m2
I = 0.09 kg m2
L = I
L = 0.72 kg m2 / s
11.34 A playground merry-go-round of radius R = 2.0 m has a moment of inertia I = 250 kg m2 and is rotating at 10 rev/min. A 25-kg child jumps onto the edge of the merry-go-round. What is the new angular speed of the merry-go-round?
Lf = Li
Li = Ii
Ii = 250 kg m2
Li = (250 kg m2) ( 10 rev/min) = 2 500 (kg m2 rev / min)
Lf = If
If = IMgR + Ichild
Ichild = m r2 = (25 kg) (2.0 m)2 = 100 kg m2
If = (250 + 100) kg m2 = 350 kg m2
11.54 A projectile of mass m moves to the right with speed vo . The projectile strikes and sticks to the end of a stationary rod of mass M and length d that is pivoted about a frictionless axle through its center.
(a) Find the angular speed of the system right after the collision.
(b) Determine the fractional loss in mechanical energy due to the collision.
Before the collision, the stationary rod has zero angular momentum and the projectil has angular momentum of
L = m v r
L = m vo (d / 2)
Li = m vo d / 2
After the collision, the rod -- with the projectile stuck to it -- rotates with angular velocity
Lf = I
I = Irod + Ipjt
Irod = (1/12) M d2
Ipjt = m (d/2)2 = (1/4) m d2
I = (1/12) M d2 + (1/4) m d2 = [(1/12) M + (1/4) m] d2
Lf = [ (1/12) M + (1/4) m] d2
Conceptual Questions
Q11.1 Is it possible to calculate the torque acting on a rigid body without specifying a center of rotation? Is the torque independent of the location of the center of rotation?
NO! It is easy to state "find the torque caused by these forces". But that is a meaningless statement. What is always required -- or meant or implied -- is "find the torque with respect to such-and-such center of rotation that is caused by these forces". Sometimes -- because of a drawing or some limitation such as the hinges on a door -- we may not specifically state that "with respect to such-and-such center of rotation" but that information is required before the statement has any meaning!
Q11.2 Is the triple produce defined by A
Explain why the operation (A
(B x C) is a vector. For convenience, let's call it vector D. That is, D = (B x C). Now our expression is A
However, since (A
Q11.3 In some motorcycle races, the riders drive over small hills, and the motorcycles become airborne for a short time. If a motorcycle racer keeps the throttle open while leaving the hill and going into the air, the motorcycle tends to nose upward. Why does this happen?
A very interesting observation!
Once the motorcycle is airborne and with the throttle still open, the rear wheel will accelerate. That means the angular momentum of the rear wheel will increase.
We can represent that as a vector pointing out of the screen,
But, while the motorcycle is airborne, the net angular momentum -- the total angular momentum of the whole "system" -- can not change. While the motorcycle is airborne there are no torques on it to change its total angular momentum. So the rest of the "system" must change angular momentum in the opposite direction,
The "rest of the system" is just the rest of the motorcycle and the rider. So they must "nose up",
Q11.4 If the torque acting on a particle about a certain origin is zero, what can you say about its angular momentum about that origin?
Its angular momentum is constant. (not necessarily zero -- just constant).
Q11.10 A scientist at a hotel sought assistance from a bellhop to carry a mysterious suitcase. When the unaware bellhop rounded a corner carrying the suitcase, it suddenly moved away from him for some unknown reason. At this point, the alarmed bellhop dropped the suitcase and ran off. What do you suppose might have been inside the suitcase?
A large, powered flywheel would have this effect. Think of trying to move a gyroscope and its response as you try to move its axis of rotation.
Q11.12 Three objects of uniform density -- a solid sphere, a solid cylinder, and a hollow cylinder -- are placed at the top of an incline as inFigure Q11.12. If they all are released from rest at the same height and roll without slipping, which object reaches the bottom first? Which reaches it last? You should try this at home and note the result is independent of the masses and the radii of the objects.
[[ Fig Q11.12 ]]
The one with the smallest moment of inertia -- or "rotational mass" -- is easiest to rotate so it will get to the bottom first. The one with the smallest moment of inertia is the solid sphere. The next is the solid cylinder. The last is the hollow cylinder.
Q11.13 A mouse is initially at rest on a horizontal turntable mounted on a frictionless vertical axle. If the mouse begins to walk around the perimeter or circumference, what happens to the turntable?
With no external torques -- because it is on a frictionless vertical axle -- the total angular momentum is conserved. That means the total angular momentum remains constant. As the mouse begins to walk around the circumference it gains angular momentum so the turntable must rotate in the opposite direction for angular momentum to counter this.
Q11.15 Often, when a high diver wants to execute a flip in midair, she draws her legs up against her chest. Why does this make her rotate faster? What should she do when she wants to come out of her flip?
Once off the board, the high diver has no torques on her so her angular momentum remains constant. Her angular momentum is the product of her moment of inertia and her angular speed. When she pulls herself into a "tuck" position, this makes her moment of inertia -- her "rotational mass" -- small. To keep the angular momentum constant the angular speed increases.
When she comes out of the "tuck" position and extends her body, this makes her moment of inertia large and her angular speed decreases to keep her angular momentum constant.
It is more fun to watch this executed by a high diver or a figure skater. But you can demonstrate the same ideas yourself on a rotating chair with a couple of heavy books in your hands. Or, we have also demonstrated this in class with a nice turntable and weights,
Solutions to the additional problems from Serway's fourth edition
(4ed) 11.1 A solid sphere has a radius of 0.200 m and a mass of 150 kg. How much work is required to get the sphere rolling with an angular speed of 50.0 rad/s on a horizontal surface? Assume the sphere starts from rest and rolls without slipping.
The moment of inertia of a solid sphere is
I = (2/5) M R2
For our particular sphere, this means
I = (2/5) (150 kg) (0.200 m)2
I = 2.4 kg m2
While it rolls along, it has kinetic energy of translation Ktr and kinetic energy of rotation Krot
KTot = Ktr + Krot = (1/2) m v2 + (1/2) I
v = r
KTot = (1/2) m v2 + (1/2) I
KTot = (1/2) (150 kg) (10 m/s)2 + (1/2) (2.4 kg m2) (50 rad/s)2
KTot = 7 500 J + 3 000 J
KTot = 10 500 J
Since work equals the change in kinetic energy and the initial kinetic energy is zero since this sphere starts from rest, this is also the work done.
W = 10 500 J
(4ed) 11.2 Verify Equation 11.14 and show that the cross product may be written as
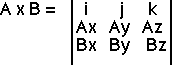First, recall what it means to expand or evaluate any determinant, Consider the following determinant:This determinant can be expanded or evaluated by making an alternating series with Cx, - Cy, and Cz, each multiplied by the cofactor of the terms remaining in the determinant when the row and column of Cx, Cy, and Cz are removed. Notice the negative sign on - Cy; that is important.These two-by-two determinants are easy to evaluate. Just remember thatThat meansandandThis meansand this is, indeed, Equation 11.14.
| Hmwk, Ch 10 | Homework Assignments | PHY 1350's Home | Hmwk, Ch 12 |
(c) Doug Davis, 2001; all rights reserved
