Ch 10, Rotation about a Fixed Axis
Homework: Ch10; 8, 20, 24, 28, 30, 39, 40, 43
Questions 4, 7, 9, 11, 14, 15, 17
| Hmwk, Ch 9 | Homework Assignments | PHY 1350's Home | Hmwk, Ch 11 |
Additional problems from Serway's fourth edition
(4ed) 10.1 The turntable of a record player rotates at a rate of 33 1/3 rev/min (rpm) and takes 60.0 s to come to rest when switched off.
Calculate (a) the magnitude of its angular acceleration
and (b) the number of revolutions it makes before coming to rest.
(4ed) 10.2 A car is traveling at 36 km/h on a straight road. The radius of the tires is 25 cm (0.25 m). Find the angular speed of one of the tires with its axle taken as the axis of rotation.
(4ed) 10.3 A can of soup has a mass of 215 g, height 10.8 cm, and diameter of 6.38 cm. It is placed at rest on the top of an inclined that is 3.00 m long and at 25o to the horizontal. Using energy methods, calculate the moment of inertia of the can if it takes 1.50 s to reach the bottom of the incline.
(4ed) 10.4 A flywheel in the shape of a solid cylinder of radius R = 0.60 m and mass M = 15 kg can be brought to an angular speed of 12 rad/s in 0.60 s by a motor exerting a constant torque. After the motor is turned off, the flywheel makes 20 rev before coming to rest because of friction (assumed constant during rotation). What percentage of the power generated by the motor is used to overcome friction?
Conceptual Questions
Q10.4 A turntable rotates at a constant rate of 45 rev/min (rpm). What is its angular speed in radians per second? What is the magnitude of its angular acceleration?
= 45 (rev/min)
= 45 (rev/min)[2 pi radians/rev]
[min/60 s]
= 45 (rev/min)[2 (3.14) radians/rev]
[min/60 s]
= 4.71 (rad/s)
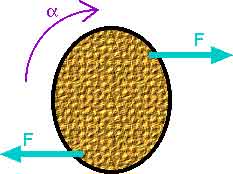
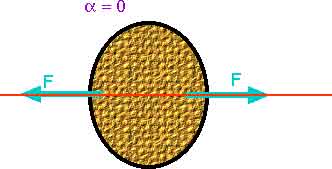
Q10.7 Suppose that only two external forces act on a rigid body and the two forces are equal in magnitude but opposite in direction. Under what condition does the body rotate?
The two forces will provide a net torque, causing rotation, unless the two forces lie along the same line.
Q10.9 Using the results from Example 10.12, how would you calculate
the angular speed of the wheel and the linear speed of the suspended mass at
t = 2 s, if the system is released from rest at t = 0? Is the expression v =
R valid in this
situation?
[[ Fig 10.20 ]]
Yes, v = R
is still valid. At the top of p 311, we have an expression for either the linear
acceleration or the angular acceleration. We can use either one of those to
find the linear velocity v or the angular velocity
and then use v = R
to find the other.
From the top of p 311, we know the linear acceleration or the angular acceleration is uniform or constant. Therefore, we can immediately use all of the kinetmatics equations for constant acceleration. In particular,
v = vo + a t
vo = 0
v = a t
v = [g/(1 + {I/mR2})] [2]
v = [2 g/(1 + (I/mR2))]
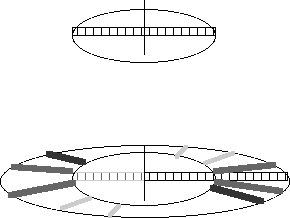
Q10.11 Explain why changing the axis of rotation of an object changes its moment of inertia.
Changing the axis of rotation changes lots of things. In particular, it changes -- or may change -- the distance through which some of the mass moves. Consider a meter stick rotated first about its center of mass and then about its end.
When the meter stick is rotated about its center of mass, both halves of the meter stick move in a circle with a maximum radius of 0.50 m.
When the meter stick is rotated about its end, one half of the meter stick still moves in this same circle. But the other half of the meter stick moves in a circle with a minimum radius of 0.50 m and a maximum radius of 1.0 m. This half of the meter stick moves through a greater distance and at a greater linear speed. All this means it is more difficult to rotate. If it is more difficult to rotate then we describe this by saying it has a greater moment of inertia -- or a greater "rotational mass".
Q10.14 Must an object be rotating to have a nonzero moment of inertia?
No. Likewise an object has a nonzero mass even when it is sitting still.
Q10.15 If you see an object rotating, is there necessarily a net torque acting on it?
If there is a net torque acting on it, the object will have an angular acceleration.
If you see an object moving, it does not necessarily have a net force acting on it.
Q10.17 The polar diameter of Earth is slightly less than the equatorial diameter. How would the moment of inertia of Earth change if some mass from near the equator were removed and transferred to the polar regions to make Earth a perfect sphere?
The mass that was at the equator that has been moved to the pole initially was far from the axis of rotation and is now very near the axis of rotation. That means the moment of inertia -- or the "rotational mass" -- of that mass is now less. That means the whole moment of inertia for Earth has decreased.
Solutions to problems from the current, fifth edition.
10.8 The tub of a washer goes into its spin cycle, starting from rest and gainiing angular speed steadily for 8.0 s when it is turning at 5.0 rev/s. At this time the person doing the laundry opens the lid and a safety switch turns off the washer. The tub smoothly slows to rest in 12.0 s. Through how many revolutions does the tub turn whil it is in motion.
Of course, we have two problems here -- how many revolutions are made as the tub speeds up and how many revolutions are made as the tub slows down? We will take each in turn.
First, how many revolutions are made as the tub speeds up? We need the
angular acceleration 
.
Since there will be a different angular acceleration as the tub slows down,
we will call this one 1.
We will use the angular equivalent of one of our "big three" kinematic equations. Just as we wrote
v2 = vo2 + 2 a s
we can also write
10.20 A car traveling on a flat (unbanked) circular track accelerates uniformly from rest with a tangential acceleration of 1.70 m/s2. The car makes it one quarter of the way around the circle before skidding off the track. Determine the coefficient of static friction between car and track.
The radius is not given so we will simply call it R and expect it to "drop out" of the answer.
v2 = vo2 + 2 a (s - so)
(s - so) = (
/ 2) R
v2 = 02 + 2 (1.70 m/s2) ( (
v2 = (5.34) R
Fc = m v2 / R
Fc = m [ 5.34 R ] / R
Fc = 5.34 m
Fc =
FN =
10.24 The center of mass of a pitched baseball (radius = 3.8 cm) moves at 38 m/s. The ball spins about an axis through its center of mass and with an angular speed of 125 rad/s. Calculate the ratio of the rotational energy to the translational kinetic energy. Treat the ball as a uniform sphere.
KTr = (1/2) M v2
KRot = (1/2) I
2
For a sphere, from Table 10.2 on p 286, I = (2/5) M R2
Ratio = KRot/ KTr = [ (1/2) I
Ratio = KRot/ KTr = [ (1/2) ((2/5) M R2)
Ratio = KRot/ KTr = [ (1/5) R2
Ratio = KRot/ KTr = (2/5) R2
Ratio = KRot/ KTr = (2/5) [ ( 0.038 m )2( 125 1/s )2 / ( 38 m/s )2
Ratio = KRot/ KTr = (2/5) [ ( 0.038 m )2( 125 1/s )2 / ( 38 m/s )2 = 0.00624
10.28 Three identical rods of length L, mass m, and radius r are placed perpendicular to each other as shown in Figure P10.22. The setup is rotated about an axis that passes through the end of one rod and is parallel to another. Determine the moment of inertia of this arrangement.
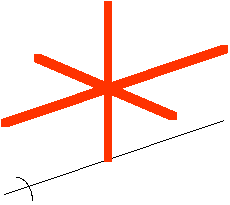
From Table 10.2, on page 286, we know the moments of intertia for a rod rotated about its center of mass and about its end,
ICM = (1/12) M L2
Iend = (1/3) M L2
We will use the parallel-axis theorem or the basic definition of moment of inertia to find additional moments of inertia as we need them. Look at the individual rods and find the moment of inertia of each of them.
Rod #1 is easy; it is just a rod rotating about its end.
I1 = Iend = (1/3) M L2
Rod #2 requires use of the parallel-axis theorem since it is being rotated about an axis parallel to an axis through its center of mass. The distance between those two axes is R = L/2.
I2 = ICM + M R2 = (1/12) M L2 + M [ (1/2) L ]2
I2 = [ (1/12) + (1/4) ] M L2
I2 = (1/3) M L2
Be careful with rod #3. It is probably easier to handle if we change our perspective and look at its motion directly along the axis of rotation.
This "rod" is also rotating along an axis parallel to an axis through its CM. But look closely at this parallel axis through its CM. For rotation about this axis, this is the rotation of a "solid cylinder". This time, ICM = (1/2) M r2. The distance between the two axes is still R = L/2.
I3 = ICM + M R2
I3 = (1/2) M r2 + M [ (1/2) L ]2
I3 = (1/2) M r2 + (1/4) M L2
As you know from lab, the total moment of inertia is the summation of the individual moments of inertia,
ITot= I1 + I2 + I3
ITot = [ (1/3) M L2 ] + [ (1/3) M L2 ] + [ (1/2) M r2 + (1/4) M L2 ]
ITot = (11/12) M L2 + (1/2) M r2
10.30 Use the parallel-axis theorem and Table 10.2 to find the moment of inertia of
(a) a solid cylinder about an axis parallel to the center-of-mass axis and passing through the edge of the cylinder and
(b) a solid sphere about an axis tangent to its surface.
(a)
For rotation about the CM,
, we know the moment of inertia.
ICM = (1/2) M R2
So we can use the parallel-axis theorem. The distance between the two axes is R.
I = ICM + M R2
I = (1/2) M R2 + M R2
I = (3/2) M R2
(b)
For rotation about the CM,
, we know the moment of inertia.
ICM = (2/5) M R2
So we can use the parallel-axis theorem. The distance between the two axes is R.
I = ICM + M R2
I = (2/5) M R2 + M R2
I = (7/5) M R2
10.39 A block of mass m1 = 2.00 kg and one of mass m2 = 6.00 kg are connected by a massless string over a pulley that is in the shape of a disk having radius R = 0.25 m and mass M = 10.0 kg. In addition, the blocks are allowed to move on a fixed block-wedge of angle theta = 30.0o as in Figure P10.29. The coefficient of kinetic friction is 0.36 for both blocks. Determine
(a) the acceleration of the two blocks and
(b) the tensions in the string.
We will (eventually) need the moment of inertia of the pulley. It is easy and straightforward to calculate so let us calculate it now. For a solid disk,
I = (1/2) M R2
I = (1/2) (10.0 kg) (0.25 m)2 = 0.3125 kg m2
Apply Newton's Second Law to each of the three bodies:
First, for mass m1:
FNet, 1 = T1 - Ff1 = m1 a
Ff1 =
T1 -
Now look at the torques on the pulley. This is not the usual "lightweight pulley" we have encountered before. You might think of this as a flywheel. It has a moment of inertia that is large enough that it can not be neglected. This also means the tension in the rope on one side of it will be different than the tension on the other side. Hence, we have labeled the tensions at T1 and T2.
net = R T2 - R T1 = I
T2 - T1 = ( I / R)
Now we are ready for the forces on m2, the mass on the incline.
Fnet = w2 sin 30o - Ff2 - T2 = m2 a
Fnet = 0.866 w2 - Ff2 - T2 = m2 a
Ff2 =
Recall that the linear acceleration of the blocks a is closely related to the angular acceleration of the pulley (or flywheel)
,
a = r
or
Now we have three equations with three unknowns, T1, T2, and a.
T1 -
T2 - T1 = ( I / R)
0.866 m2 g - 0.50
Now we can put in numbers and then solve for the unknowns.
T1 - (0.36) (2.0 kg) (9.8 m/s2) = (2.0 kg) a
T2 - T1 = [ 0.3125 kg m2 / (0.25 m)2 ] a = 5 kg a
0.866 (6.0 kg) (9.8 m/s2) - 0.50 (0.36) (6.0 kg) (9.8 m/s2) - T2 = (6.0 kg) a
50.92 N - 10.58 N - T 2 = (6.0 kg) a
T1 - 7.056 N = (2.0 kg) a
T2 - T1 = 5 kg a
40.34 N - T 2 = (6.0 kg) a
T1 = 7.056 N + (2.0 kg) a
T2 - [7.056 N + (2.0 kg) a] = 5 kg a
T2 = [7.056 N + (2.0 kg) a] + 5 kg a
T2 = 7.056 N + (7.0 kg) a
40.34 N - T 2 = (6.0 kg) a
40.34 N - [7.056 N + (7.0 kg) a] = (6.0 kg) a
40.34 N - 7.056 N = (7.0 kg) a + (6.0 kg) a
33.28 N = (13.0 kg) a
a = 33.28 N / 13.0 kg
a = 2.56 m / s2
T2 = 7.056 N + (7.0 kg) a = 7.056 N + (7.0 kg) (2.56 m/s2) = 25 N
T1 = 7.056 N + (2.0 kg) a = 7.056 N + (2.0 kg) (2.56 m/s2) = 12.2 N
10.40 A potter's wheel, a thick stone disk of radius 0.50 m and mass 100 kg, is freely rotating at 50 rev/min. The potter can stop the wheel in 6.0 s by pressing a wet rag against the rim and exerting a radially inward force of 70 N. Find the effective coefficient of friction between wheel and wet rag.
t
This angular acceleration is produced by a torque due to the friction force exerted by the potter with the wet rag.
Ff =
To evaluate this numerically, we need the numerical value of the moment of inertia for the potter's wheel.
I = (1/2) M R2 = 0.5 (100 kg) (0.50 m)2 = 12.5 kg m2
or
Ff =
Ff =
or
10.43 A 15-kg mass and a 10-kg mass are suspended by a pulley that has a radius of 10 cm and a mass of 3.0 kg (Fig P10.32). The cord has a negligible mass and causes the pulley to rotate without slipping. The pulley rotates without friction. The masses start from rest 3.0 m apart. Treat the pulley as a uniform disk and detemine the speeds of the two masses as they pass each other.
Now, draw free-body diagrams for all three bodies,
We will need the moment of inertia of the pulley,
I = (1/2) M r2 = (0.5) (3.0 kg) (0.10 m)2 = 0.015 kg m2
For mass m2, I have taken up to be positive; that means
Fnet,2 = T2 - m2 g = m2 a
For the pulley,
(0.10 m) [ T1 - T2 ] = I
The linear acceleration a and the angular acceleration
a = r
or
so we may write
(0.10 m) [ T1 - T2 ] = (0.015 kg m2) a / 0.10 m
(0.10 m) [ T1 - T2 ] = (0.15 kg m) a
T1 - T2 = (1.5 kg) a
And, for mass m1, where I have taken down as positive,
FNet,1 = m1 g - T1 = m1 a
(15.0 kg) (9.8 m/s2) - T1 = (15.0 kg) a
147 N - T1 = (15.0 kg) a
Now we have three equations -- from the three free-body diagrams -- and three unknowns.
T1 = 147 N - (15.0 kg) a
T1 - T2 = (1.5 kg) a
[ 147 N - (15.0 kg) a] - T2 = (1.5 kg) a
T2 = [ 147 N - (15.0 kg) a] - (1.5 kg) a
T2 = 147 N - (16.5 kg) a
T2 - m2 g = m2 a
[147 N - (16.5 kg) a] - (10.0 kg) (9.8 m/s2) = (10.0 kg) a
147 N - 98 N = (26.5 kg) a
a = 49 N / 26.5 kg
a = 1.85 m/s2
With this acceleration of 1.85 m/s2, how fast will the blocks be moving after they have moved a distance of 1.5 m?
v2 = vo2 + 2 a (y - yo)
v2 = 02 + 2 (1.85 m/s2) (1.5 m)
v2 = 5.55 m2 / s2
v = 2.36 m/s
Solutions to the additional problems from Serway's fourth edition
(4ed) 10.1 The turntable of a record player rotates at a rate of 33 1/3 rev/min (rpm) and takes 60.0 s to come to rest when switched off.
Calculate (a) the magnitude of its angular acceleratin
and (b) the number of revolutions it makes before coming to rest.
-
(4ed) 10.2 A car is traveling at 36 km/h on a straight road. The radius of the tires is 25 cm (0.25 m). Find the angular speed of one of the tires with its axle taken as the axis of rotation.
v = vt = r
v = 36 km/hr [ 1 hr / 3 600 s] [ 1 000 m / 1 km ] = 10 m/s
(4 ed) 10.3 A can of soup has a mass of 215 g, height 10.8 cm, and diameter of 6.38 cm. It is placed at rest on the top of an inclined that is 3.00 m long and at 25o to the horizontal. Using energy methods, calculate the moment of inertia of the can if it takes 1.50 s to reach the bottom of the incline.
vavg = 3.0 m / 1.5 s = 2 m/s
vf = 2 vavg = 4 m/s
Ei = Ui + K i = m g h i + 0 = m g h i
Ef = Uf + K f = 0 + KTot = KTot = KTr + KRot
KTot = KTr + KRot = (1/2) m v2 + (1/2) I
Ef = Ei
Ef = KTot = Kf = Ui = m g hi = Ei
hi = ( 3.0 m ) sin 25o = (3.0 m) (0.4226) = 1.268 m
Ei = m g h i = (0.215 kg) (9.8 m/s2)(1.268 m) = 2.67 J
Ef = KTot = (1/2) (0.215 kg) v2 + (1/2) I
vavg = 3.0 m / 1.5 s = 2.0 m/s
vavg = (vo + v)/2 = (0 + v )/2 = v/2
v = 2 vavg = 2 (2.0 m/s) = 4.0 m/s
v = r
Ef = KTot = (1/2) (0.215 kg) (4.0 m/s)2 + (1/2) I (125.4 rad/s)2 = 2.67 J = Ei
1.72 J + (7 862.6 1/s2) I = 2.67 J
(7 862.6 1/s2) I = 0.95 J
I = 0.000121 J s 2
What is a "J s2"?
J s 2 = J s 2 [ N m / J ] [ (kg m/s2) / N ] = kg m 2
and, of course, those are just the units we would expect for a moment of inertia.
I = 0.000121 kg m2
For confidence -- and for practice -- what would be the moment of inertia of this soup can if it were a solid cylider?
I = (1/2) M R2
I = (1/2) (0.215 kg) (0.0319 m)2
I = 0.00011 kg m2
And that is reasonably close to the value we calculated for our can of liquid soup.
(4ed) 10.4 A flywheel in the shape of a solid cylinder of radius R = 0.60 m and mass M = 15 kg can be brought to an angular speed of 12 rad/s in 0.60 s by a motor exerting a constant torque. After the motor is turned off, the flywheel makes 20 rev before coming to rest because of friction (assumed constant during rotation). What percentage of the power generated by the motor is used to overcome friction?
For such a solid cylinder, rotating about its CM, we know the moment of inertia
I = (1/2) M R2
I = (1/2) (15 kg) (0.60 m)2
I = 2.7 kg m2
K = (1/2) I
K = 525 kg m2 / s2 = 525 J
W = P
W = P (0.60 s) = 525 J + Wfriction
Wfriction = Pfriction (0.60 s)
P (0.60 s) = 525 J + Pfriction (0.60 s)
While friction brings it to a stop it has an angular acceleration
02 = (12 rad/s)2 + 2
02 = (12 rad/s)2 + 2
Remember, this is the angular acceleration due to the torque caused by friction. How is this related to power?
Just as P = F v for the linear case, we can write P =
Pf =
Pf = ( - 1.547 N m )
Pf, avg = ( - 1.547 N m )
During start-up, we found
P (0.60 s) = 525 J + Pfriction (0.60 s)
P (0.60 s) = 525 J + ( - 1.547 N m )
P (0.60 s) = 525 J + ( - 1.547 N m ) (6 rad/s) (0.60 s)
P (0.60 s) = 525 J - 5.57 J
P (0.60 s) = 519.4 J
P = 519.4 J / 0.60 s = 866 W
This is the power supplied by the motor. How much is absorbed by friction?
P f =
P f = 525 J /
We know the flywheel stops after 20 revolutions. But we do not (yet) know what this is in terms of time. We can find that from
0 = 12 rad/s + ( - 0.573 rad/s2 ) t
t = (12 / 0.573) s
t = 20.94 s
P f = 525 J /
P f = 525 J / 20.94 s
P f = 25.1 W
We've done all the hard work. Now we can easily finish up with
Ratio = P f / PTot = Pf / P = (25.1 W) / (866 W) = 0.0289
Ratio = 0.0289
| Hmwk, Ch 9 | Homework Assignments | PHY 1350's Home | Hmwk, Ch 11 |
(c) Doug Davis, 2001; all rights reserved
