

Ch 12; Static Equilibrium
Homework: Ch12; 1, 2, 7, 20, 21, 22, 30, 38, 42, 43, 51
Questions 4, 5, 9, 10, 11, 12
| Hmwk, Ch 11 | Homework Assignments | PHY 1350's Home | Hmwk, Ch 13 |
Additional problem from Serway's fourth edition
(4ed) 12.* A steel piano wire 1.12 m long has a cross-sectional area of 6.0 x 10-3 cm2. When under a tension of 115 N, how much does it stretch?
From Table 12.1, p 346, Young's modulus for steel is 20 x 1010 N / m2.
A = 6.0 x 10-3 cm2 [ 1 m2 / 104 cm2 ] = 6.0 x 10-7 m2
stress = F / A = 115 N / 6.0 x 10-7 m2
F / A = 1.92 x 108 N / m2
Conceptual Questions
Q12.4 The center of gravity of an object may be located outside the object. Give a few examples for which this is the case.
Pay attention. This is essentially Question 9.12 restated. There we found examples of a donut, a carpenter's square, and a pole vaulter.
Q12.5 You are given an arbitrarily shaped piece of plywood, together with a hammer, nail, and plum bob. How could you use the items to locate the center of gravity of the plywood?
If you suspend the arbitrarily shaped piece of plywood so it can rotate, the center of mass will end up directly below the point of support. You can hang the plumb bob or plumb line from that point of suport and draw a line along the plumb line. The CoM is somewhere on that line. Then hang the piece of plywood from another point and do this again. The CoM is at the intersection of those two lines. You might want to "check" this by suspending it from a third point and ensure that the three lines intersect a a common point as they should.
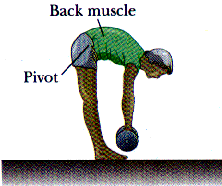
Q12.9 When lifting a heavy object, why is it recommended to keep the back as vertical as possible, lifting from the knees rather than bending over and lifiting from the waist?
This reduces the forces exerted by the back muscles -- the forces on your spine.
Q12.10 Give a few examples in which several forces are acting on a system in such a way that their sum is zero but the system is not in equilibrium.
This, too, is similar to a previous question, Question 10.7. If two forces in opposite directions, but of equal magnitude and not along the same line, act on an object, their net force is zero so the object does not accelerate. However, these forces still exert a net torque on the object so that it has an angular acceleration.
Q12.11 If you measure the net torque and the net force on a system to be zero,
(a) Could the stystem still be rotating with respect to you?
A net torque of zero means there will be no angular acceleration but the angular velocity does not need to be zero.
(b) Could it be translating with respect to you?
Translating has noting to do with net torque so, yes, it could well be translating.
Q12.12 A ladder is resting inclined against a wall. Would you feel safer climbing up the ladder if you were told that the ground is frictionless but the wall is rough or that the wall is frictionless but the ground is rough?
A frictionless surface can still exert a normal (perpendicular!) force.
Consider torques about the Center of Mass. About that as the center of rotation, the climber's weight creates a clockwise torque. Friction from the floor will create a counter-clockwise torque to balance that.
I would want a rough floor.
Problem solutions
12.1 A baseball player holds a 36-oz bat (weight = 10.0 N) with one hand at the point O (Fig P12.1). The bat is in equilibrium. The weight of the bat acts along a line 60 cm (or 0.60 m) to the right of O. Determine the force and torque exerted on the bat by the player.

The first condition of equilibrium is that the sum of all the forces must be zero.

Fext = w
The second condition of equilibrium is that the sum of the torques is zero or the sum of the clockwise torques equals the sum of the counter clockwise torques. We will measure torque about the point O.
ccw =
cw
ccw =
ext = (0.60 m) (10.0 N) =
cw
ext = 6.0 m-N
12.2 Write the necessary conditions of equilibrium for the body shown in Figure P12.2. Take the origin of the torque equation at the point O.
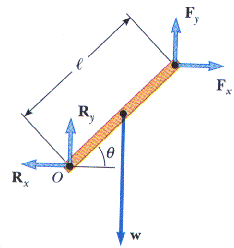
![]() Fx =
Fx - Rx = 0
Fx =
Fx - Rx = 0
![]() Fy =
Fy + Ry - w = 0
Fy =
Fy + Ry - w = 0
![]()
![]() ccw =
ccw = ![]()
![]() cw
cw
Torques will be calculated about point O the lower left end of the rod
Rx:
= 0
Ry:
= 0
w:
=
cw = (L / 2) (w) sin (180o -
) = (L / 2) (w) cos
Fx :
=
cw = (L) (Fx ) sin
Fy :
=
ccw = (L) (Fy ) sin (180o -
) = (L) (Fy ) cos
ccw =
cw
ccw = (L) (Fy ) cos
=
= (L) (Fx ) sin
+ (L / 2) (w) cos
=
cw
12.7 A carpenter's square has the shape of an "L", as in Figure P 12.8. Locate its center of gravity.
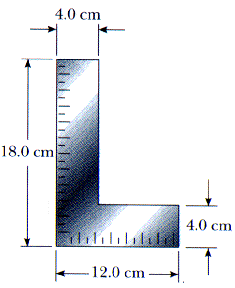
Treat this as two rectangular objects.
Now this is just finding the center of mass of a two-mass system.
X = [ X1 mx + X2 m2 ] / [ m1 + m2 ]
X = [(2)(72) + (8)(22)] / [72 + 32]
X = 3.1 cm
Y = [ Y1 mx + Y2 m2 ] / [ m1 + m2 ]
Y= [(9)(72) + (2)(22)] / [72 + 32]
Y = 6.7 cm
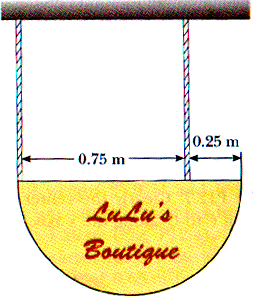
12.20 A hemispherical sign 1.0 m in diameter and of uniform mass density is supported by two strings as shown in Figure P12.19. What fraction of the sign's weight is supported by each string?
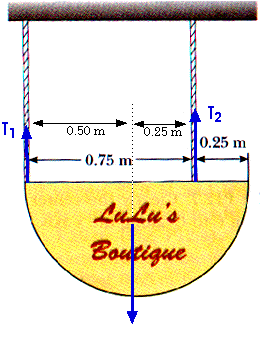
Fy = T1 + T2 - W = 0
T1 + T2 = W
ccw =
cw
We will calculate torques about the left edge.
T1:
= 0
T2:
=
ccw = (0.75 m) T2
W:
=
cw= (0.50 m) W
ccw =
cw
(0.75 m) T2 = (0.50 m) W
T2 = 0.67 W
T1 = 0.33 W
12.21 Sir Lost-a-Lot dons his armor and sets out from the castle on his trusty steed in his quest to rescue fair damsels from dragons (Fig P12.20). Unfortunately his aide lowered the drawbridge too far and finally stopped it 20.0o below the horizontal. Sir Lost and his steed stop when their combined center of mass is 1.0 m from the end of the bridge. The bridge is 8.0 m long and has a mass of 2 000 kg; the lift cable is attached to the bridge 5.0 m from the castle end and to a point 12.0 m above the bridge. Sir Lost's mass combined with his armor and steed is 1 000 kg.
(a) Determine the tension in the cable and
(b) the horizontal and vertical force components acting on the bridge at the castle end.

First, a free-body diagram showing all the forces involved.
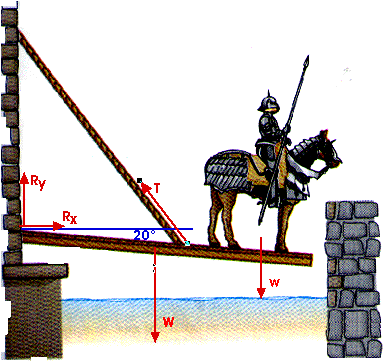
My diagrams quickly became fairly messy so I have spread some of this information over two or three diagrams. Above, the free-body diagram shows all the forces. Below, I have added vectors and dimensions, showing where the forces are applied.
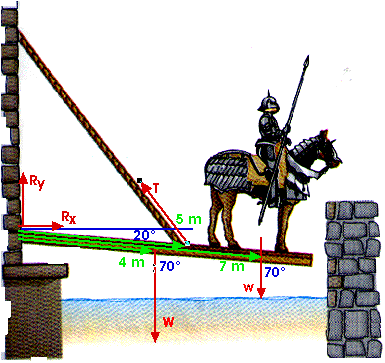
It is always possible that I have made things more difficult than they need to be. But it was interesting and fun(!?) to find the angle of 44.2o between the drawbridge in its present position and the cable. It involves a triangle that is not a right triangle so I had to go back to "Law of Sines" and the "Law of Cosines" that I have not used for quite a while. A Physicist's (or an Engineer's) bag of tools includes lots of thing from lots of math courses that should not be forgotten. This angle of 44.2 o is the angle between the drawbridge and the cable. The angle between the horizontal and the cable is 64.2 o.
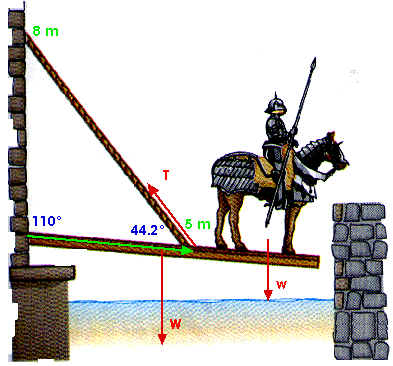
Now we are ready to start applying the two conditions of equilibrium. Be careful with all the angles.
The first condition of equilibrium is that the vector sum of all the forces equals zero.
Fx = 0
Fx = Rx - T cos 64.2 o = 0
Rx = T cos 64.2 o = 0.435 T
Fy = 0
Fy = Ry + T sin 64.2 o - W - w = 0
W = (2 000 kg) (9.8 m/s2) = 19 600 N
w = (1 000 kg) (9.8 m/s2) = 9 800 N
Ry + 0.900 T sin 64.2 o = 29 400 N
As we should expect by now, at this stage, we have three unknowns -- Rx, Ry, and T -- but only two equations. We will get the third equation from applying the second condition of equilibrium, that the sum of the torques must equal zero. We will calculate the torques about the hinge of the drawbridge.
Rx:
= 0
Ry:
= 0
T:
=
ccw = (5 m) T sin 44.2o = (5 m) (T) (0.697) =
= 3.49 m T
W:
=
cw = (4 m) (19 600 N) sin 90o = 78 400 N-m
w:
=
cw = (7 m) (9 800 N) sin 90o = 68 600 N-m
ccw =
cw
3.49 m T = 147 000 N-m
T = 42 120 N
Now that the tension is known, we can go back and determine the "reaction force" Rx and Ry,
Rx = 0.435 T
Rx =18 322 N
Ry = 29 400 N - 0.900 T sin 64.2 o
Ry = 29 400 N - 34 129 N
Ry = - 4 729 N
What does this negative sign mean? When I guessed that Ry pointed up, I guessed wrong! The forces are such -- and they are located such -- that the hinge exerts a downward force so Ry points down and that is shown by the negative value we calculate for Ry.
12.22 Two identical uniform bricks of length L are placed in a stack over the edge of a horizontal surface with the maximum overhand possible without falling, as in Figure P12.21. Find the distance x.
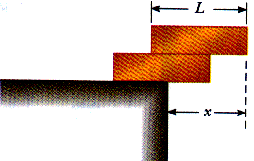
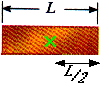
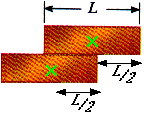
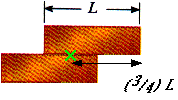
The center of gravity must remain above the point of support; therefore,
x = ( 3/4) L
12.38 A letter "A" is formed from two uniform pieces of metal each of weight 26.0 N and length 1.00 m, hinged at the top and held together by a horizontal wire of length 1.20 m (Fig P12.4). The structure rests on a frictionless surface. If the wire is connected at points a distance of 0.65 m from the top of the letter, determine the tension in the wire.
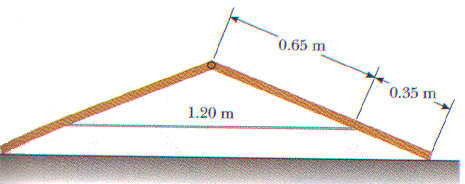
Make a free-body diagram of the forces acting on say the right member. We could make a similar free-body diagram of the forces acting on the left member. By symmetry they will be mirror images of each other.
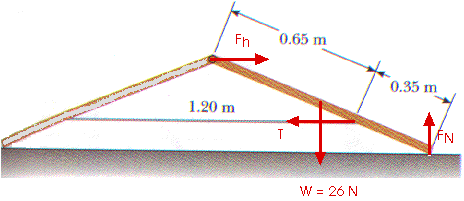
Fh is the horizontal force supplied by the left member acting on the right member.
T is the tension in the cable (and the value asked for in this question)
W is the weight of the member 26 N an is located at the center of mass 0.50 m from the hinge.
FN is the normal force exerted by the floor on the member.
Now apply the two conditions of equilibrium:
The sum of all the forces must be zero.
Fx = Fh - T = 0
Fh = T
Fy = FN - W = 0
FN - 26 N = 0
FN = 26 N
This provides only two equations while we have three unknowns. Or since FN is fully known we have only one equation Fh = T but two unknowns. We need more information; . . .
The second condition of equilibrium is that
The sum of all the torques must be zero.
ccw =
cw
With a little geometry we can calculate the angles as shown.
We will now calculate torques about the hinge:
Fh:
= 0
W:
=
cw = (0.50 m)(26 N) sin 67.4o = 12 N-m
T:
=
cw = (0.65 m)( T ) sin 22.6o = 0.25 m T
FN:
=
ccw = (1.0)( FN ) sin 67.4o = 0.92 FN
=
ccw = (1.0)( 26 N ) sin 67.4o = 24 N-m
ccw =
cw
24 N-m = 0.25 m T + 12 N-m
0.25 m T = 12 N-m
T = 48 N
And we already know Fh = T so we now know all the forces involved.
12.30 A 2.0-m-long cylinderical steel wire with a cross-sectional diameter of 4.0 mm is placed over a frictionless pulley, with one end of the wire connected to a 5.00 kg mass and the other end connected to a 3.00 kg mass. By how much does the wire stretch while the masses are in motion?
This starts out as another Atwood's machine problem.
a = ( m1 - m2 ) g / ( m1 + m2 )
a = (2 kg) (9.8 m/s2) / (8 kg)
a = 2.45 m/s2
To provide this acceleration, the tension in the wire must be
Fnet,1 = T - (3 kg)(9.8 m/s2) = 3 kg (2.45 m/s2)
T = 36.75 N
A =
r2 =
(0.002 m)2 = 1.26 x 10-5 m2
(a) Draw a free-body diagram for the beam.
(b) When the bear is at x = 1.00 m, find the tension in the wire and the components of the force exerted by the wall on the left end of the beam.
(c) If the wire can withstand a maximum tension of 900 N, what is the maximum distance the bear can walk before the wire breaks?
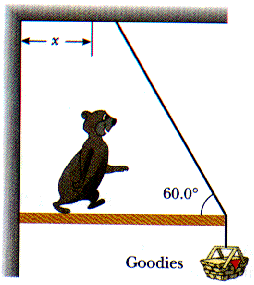
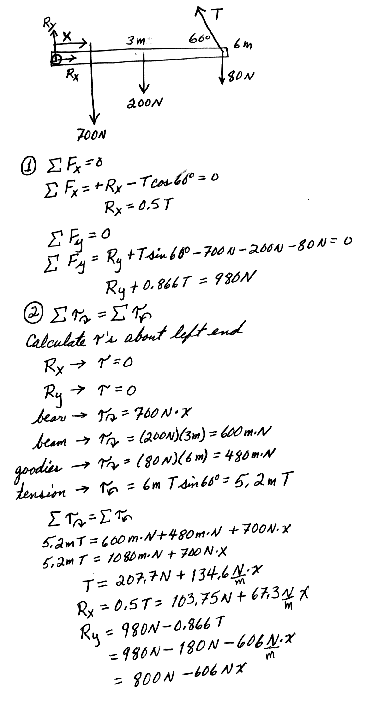
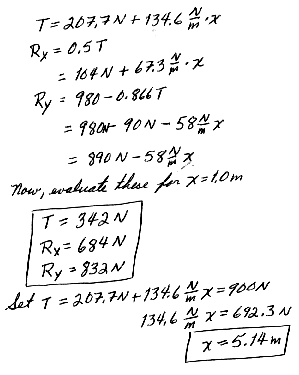
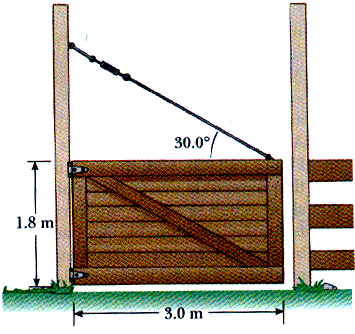
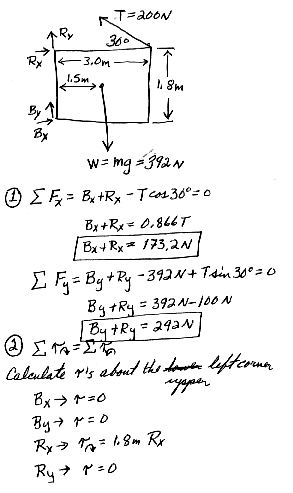
12.43 Old MacDonald had a farm, and on that farm he had a gate (Fig P12.43). The gate is 3.0 m long and 1.8 m tall with hinges attached to the top and bottom. The guy wire makes an angle of 30.0o with the top of the gate and is tightened by turnbuckle to a tension of 200 N. The mass of the gate is 40.0 kg.
(a) Determine the horizontal force exerted on the gate by the bottom hinge.
(b) Find the horizontal force exerted by the upper hinge.
(c) Determine the combined vertical force exerted by both hinges.
(d) What must be the tension in the guy wire so that the horizontal force exerted by the upper hing is zero?
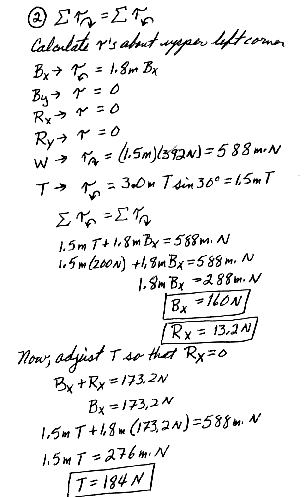
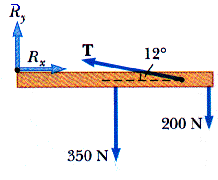
12.51 A person bends over and lifts a 200-N object as in Figure P12.45a, with the back in the horizontal position (a terrible way to lift an object). The back muscle attached to a point two-thirds up the spine maintains the position of the back, where the angle between the spine and this muscle is 12.0o. Using the mechanical model shown in Figure P12.45b and taking the weight of the upper body to be 350 N, find the tension in the back muscle and the compressional force in the spine.
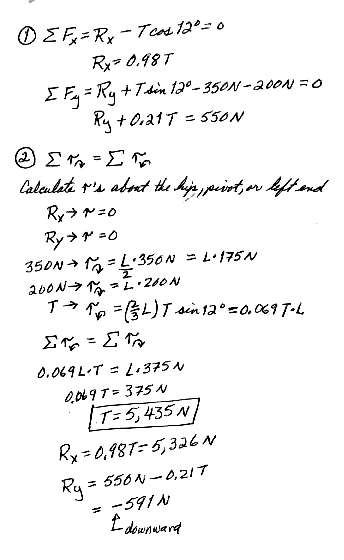
| Hmwk, Ch 11 | Homework Assignments | PHY 1350's Home | Hmwk, Ch 13 |
(c) Doug Davis, 2001; all rights reserved