Additional problems from Serway's fourth edition
(4ed) 9.1 A superball with a mass of 60 g is dropped from a height of 2.0 m. It rebounds to a height of 1.8 m. What is the change in its linear momentum during the collision with the floor?
(a) Determine the two velocities just before the collision.
(b) Using Equations 9.20 and 9.21, determine the two velocities immediately after the collision.
(c) Determine the maximum height to which each block rises after the collision.
Conceptual Questions
Q9.12 Can the center of mass of a body lie outside the body? If so, give examples.
Yes! The center of mass does not need to lie within a body.
The center of mass of a donut is in the center -- where the hole is!
The center of mass of a carpenter's square is outside of the square.
As a pole vaulter or high jumper goes over the bar, their center of mass will probably pass under the bar.
Q9.14 A meter stick is balanced in a horizontal position with the index fingers of the right and left hands. If the two fingers are slowly brought together, the stick remains balanced and the two fingers always meet at the 50-cm mark, regardless of their original positions (Try it!). Explain.
This one is fun and it really works. Indeed, it is worth trying yourself!
As you move your fingers together, the one closest to the center of mass (CoM) exerts the greater upward force. That also means it has the greater friction force between it and the meter stick. So the one farther from the CoM has less friction and slides more easily. This means they both end up at the CoM, the 50-cm mark!
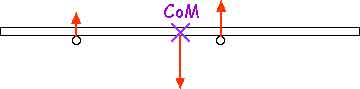
Q9.15 A sharpshooter fires a rifle while standing with the butt of the gun against his shoulder. If the forward momentum of a bullet is the same as the backward momentum of the gun, why is it not as dangerous to be hit by the gun as by the bullet?
The masses of the bullet and gun are quite different so the speeds or velocities are quite different. The gun recoils with far less speed than that of the bullet. Remember that the Kinetic Energy goes like the square of the speed, KE = (1/2) m v2. This means the gun, with its slower speed, carries far less energy than the bullet.
Q9.22 A bomb, initially at rest, explodes into several pieces.
(a) Is linear momentum conserved?
Yes; linear momentum is always conserved.
Initially, the linear momentum was zero. After the collision the linear momentum -- the vector sum of all of the linear momentum of all the parts -- will remain zero. Some part may move in one direction, carrying linear momentum with it. But another part -- or several other parts -- will carry linear momentum in the opposite direction.
(b) Is kinetic energy conserved?
No, the kinetic energy is not conserved. Energy stored as chemical energy (a very special form of potential energy) is converted into kinetic energy as the bomb explodes!
Problems from the current (5th) edition of Serway and Beichner
9.6 Two blocks of masses M and 3 M are placed on a horizontal, frictionless surface. A light spring is attached to one of them and the blocks are pushed together with the spring between them, as in Figure P9.6. A cord initially holding the blocks together is burned; after this, the block of mass 3 M moves to the right with a speed of 2.0 m/s.
(a) What is the speed of the block of mass M?
(b) Find the original elastic energy in the spring if M = 0.350 kg.
[[ Fig P9.6 ]]
Pfinal = Pinitial
Pinitial = 0
Pfinal = M ( - vleft) + 3 M (2.0 m/s) = 0
M vleft = 3 M (2.0 m/s)
vleft = 3 (2.0 m/s)
vleft = 6.0 m/s
Einitial = Eelastic(spring) = (1/2) k x2
Efinal = KETotal = (1/2)(M)(vleft)2 + (1/2)(3 M)(vright)2
Efinal = KETotal = (1/2)(0.350 kg)(6.0 m/s)2 + (1/2)(1.050 kg)(2.0 m/s)2
Efinal = KETotal = 8.4 J
Therefore,
Einitial = Eelastic(spring) = 8.4 J
9.10 A tennis player receives a shot with the ball (0.060 kg) traveling horizontally at 50 m/s and returns the shot with the ball traveling horizontally at 40 m/s in the opposite direction. What is the impulse delivered to the ball by the racket?
po = m vo = (0.060 kg) (50 m/s) = 3.0 kg m/s pf = m vf = (0.060 kg) ( - 40 m/s) = - 2.4 kg m/s
p = pf - po = - 2.4 kg m/s - 3.0 kg m/s
9.11 A 3.0-kg steel ball strikes a wall with a speed of 10 m/s at an angle of 60o with the surface. It bounces off with the same speed and angle (Fig. P9.15). If the ball is in contact with the wall for 0.20 s, what is the average force exerted on the ball by the wall?
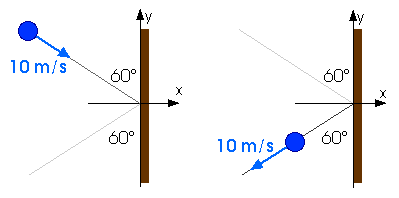
Fy = dpy/dt Fx = dpx/dt
Only the x-component of the momentum is changed. The y-component remains the same so Fy = 0.
Fx = dpx/dt = px,i = m vx,i = (3.0 kg) (10 m/s) sin 60o
sin 60o = 0.866
px,i = (3.0 kg) (10 m/s) (0.866) = 26.0 kg m/s
px,f = m vx,f = - (3.0 kg) (10 m/s) sin 60o
px,f = - (3.0 kg) (10 m/s) (0.866) = - 26.0 kg m/s
Fx =
Fx = ( - 52 kg m/s ) / (0.20 s)
Fx = - 260 N
The negative sign means the force exerted on the ball is directed to the left.
9.17 A 10.0-g bullet is fired into a stationary block of wood (m = 5.0 kg). The relative motion of the bullet stops inside the block. The speed of the bullet-plu-wood combination immediately after the collision is measured as 0.600 m/s. What was the original speed of the bullet?
Pinitial = Pfinal
Pinitial = mbullet vbullet + Mblock + vblock
Pinitial = (10 g) vbullet + 0
Pfinal = Mcombo vcombo
Pfinal = (5 010 g)(0.60 m/s)
Pfinal = 3 006 g-m/s
Pinitial = Pfinal
Pinitial = (10 g) vbullet = 3 006 g-m/s
vbullet = 300.6 m/s
(a) What is the velocity of the truck right after the collision?
(b) How much mechanical energy is lost in the collision?
Account for this loss in energy.
Momentum must be conserved.PTot,i = p1i + p2i PTot,i = (1 200 kg) (25.0 m/s) + (9 000 kg) (20.0 m/s)
PTot,i= 210 000 kg m/s
PTot,i = = p1f + p2f
PTot,f = (1 200 kg) (18.0 m/s) + (9 000 kg) v
We are trying to find velocity v.
PTot,f = PTot,i (1 200 kg) (18.0 m/s) + (9 000 kg) v = 210 000 kg m/s
21 600 kg m/s + (9 000 kg) v = 210 000 kg m/s
(9 000 kg) v = 188 400 kg m/s
v = 20.9 m/s
KTot,i = K1i + K2i
KTot,i= (1/2) m1 v1i2 + (1/2) m2 v2i2
KTot,i = (1/2) (1 200 kg) (25.0 m/s)2 + (1/2) (9 000 kg) (20.0 m/s)2
KTot,i = 375 000 J + 1 800 000 J
KTot,i = 2 175 000 J
KTot,f = K1f + K2f
KTot,f= (1/2) m1 v1f2 + (1/2) m2 v2f2
KTot,f = (1/2) (1 200 kg) (18.0 m/s)2 + (1/2) (9 000 kg) (20.9 m/s)2
KTot,f = 194 400 J + 1 965 645 J
KTot,f = 2 160 045 J
This kinetic energy that is "lost" -- as far as large-scale, macro-motion is concerned -- goes into bending the sheet metal of the car and truck. A little is converted into sound.
9.22 A railroad car of mass 2.50 x 104 kg is moving with a speed of 4.00 m/s. It collides and couples with three other coupled railroad cars, each of the same mass as the single car and moving in the same direction with an initial speed of 2.00 m/s.
(a) What is the speed of the four cars after the collision?
(b) How much energy is lost in the collision?
Pfinal = Pinitial
Even tho' we are told the mass of the railroad cars, it is a bit easier at this point to just write it as M. We will need the actual mass, tho', to answer part (b).
Pfinal = 4 M vfinal
Pinitial = M (4.0 m/s) + 3 M (2.0 m/s)
Pfinal = 4 M vfinal = M (4.0 m/s) + 3 M (2.0 m/s) = Pinitial
4 vfinal = (4.0 m/s) + 3 (2.0 m/s) = 10.0 m/s
4 vfinal = 10.0 m/s
vfinal = 2.5 m/s
When the author asks "how much energy is 'lost'", of course that really means "how much kinetic energy is 'lost' to become heat"?
E'lost' = Einitial - Efinal
Einitial = (1/2)(2.5 x 104 kg)(4.0 m/s)2 + (1/2)(3 x 2.5 x 104 kg)(2.0 m/s)2
Einitial = 3.5 x 105 J
Efinal = (1/2)(4 x 2.5 x 104)(2.5 m/s)2
Efinal = 3.125 x 105 J
E'lost' = Einitial - Efinal
E'lost' = (3.500 - 3.125) x 105 J
E'lost' = 0.375 x 105 J
E'lost' = 3.75 x 104 J
9.36 Two shuffleboard disks of equal mass, one orange and the other yellow, are involved in a perfectly elastic, glancing collision. The yellow disk is initially at rest and is struck by the orange disk moving with a speed of 5.00 m/s. After the collision, the orange disk moves along a direction that makes an angle of 37.0o with its initial direction of motion, and the velocity of the yellow disk is perpendicular to that of the orange disk (after the collision -- and this will always be the case for elastic collisions between equal masses). Determine the final speed of each disk.
Separately, the x- and y-components of the total momentum are conserved.
Pxi = m vorg,o + m vyel,o Pxi = m vo + 0 = m (5.0 m/s) + 0
Pxi = m vo
Pyi = . . . = 0
We can substitute 5.0 m/s = vo at the end.
Pfx = m vorg,x + m vyel,x Pfx = m vorg cos 37o + m vyel cos 53o
Pfx = m vorg (0.8) + m vyel (0.6)
Pfx = m [ vorg (0.8) + vyel (0.6) ]
Pfx = m [ vorg (0.8) + vyel (0.6) ] = m vo = Pix
vorg (0.8) + vyel (0.6) = vo
Of course, this is one equation with two unknowns so we need some additional information. We will get that from looking at the y-equation for the conservation of momentum.
Now, for the y-component,
Pfy = m vorg,y + m vyel,y Pfy = m vorg sin 37o - m vyel sin 53o
Pfy = m vorg (0.6) - m vyel (0.8)
Pfy = m [ vorg (0.6) - vyel (0.6) ]
Pfy = m [ vorg (0.6) - vyel (0.8) ] = 0 = Piy
[ vorg (0.6) - vyel (0.8) ] = 0
Now we have two equations and two unknowns, vorg and vyel.
0.6 vorg = 0.8 vyel vorg = 1.333 vyel
vorg (0.8) + vyel (0.6) = vo
(0.8)(1.33 vyel ) + 0.6 vyel = vo
1.667 vyel = vo
vyel = 0.6 vo
vyel = 0.6 (5.0 m/s) = 3.0 m/s
vorg = (1.333) (3.0 m/s)
vyel = 4.0 m/s
9.47 Romeo (77.0 kg) entertains Juliet (55.0 kg) by playing his guitar from the rear of their boat at rest in still water, 2.70 m away from Juliet who is in the front of the boat. After the serenade, Juliet carefully moves to the rear of the boat (away from the shore) to plant a kiss on Romeo's cheek. How far does the 80.0-kg boad move toward the shore it is facing?
|
|
The center of mass of the total system does not move. We will measure distances from Romeo or we will use Romeo as the orgin of our coordinate system. Notice that we do not know where the center of mass of the boat is. We will just put that in as Xboat and expect it to drop out of the calculations. Actually, what we need is XRb the center of mass of Romeo and the boat. Xtot = [XRb MRb + XJ MJ]/Mtot Initially, Xtot = [XRb (157 kg) + XJ (55 kg)]/212 kg XJ = 2.7 m After Juliet moves to Romeo, Xtot = [(x +XRb)(157 kg) + (x) (55 kg)]/212 kg Remember, the center of mass of the total system does not move. Therefore, [XRb (157 kg) + XJ (55 kg)]/212 kg = [(x +XRb)(157 kg) + (x) (55 kg)]/212 kg [XRb (157 kg) + (2.7 m) (55 kg)] = [(x +XRb)(157 kg) + (x) (55 kg)] XRb (157) + (2.7 m) (55) = [(x +XRb)(157) + (x) (55)] 157 XRb + 148.5 m= 157 x + 157 XRb + 55 x Notice that the XRb term does, indeed, drop out -- just as we expected it to. 148.5 m= 157 x + 55 x 212 x = 148.5 m x = 148.5 m / 212 x = 0.70 m |
|
9.51 The first stage of a Saturn V space vehicle consumes fuel and oxidizer at the rate of 1.50 x 104 kg/s with an exhaust speed of 2.60 x 103 m/s.
(a) Calculate the thrust produced by these engines.
(b) Find the initial acceleration of the vehicle on the launch pad if its itinital mass is 3.0 x 106 kg.
From Eq 9.42 on p 279, we know
Thrust = | ve (dM/dt) |
The absolute value bars are in this equation because (dM/dt) < 0 as the mass of the rocket decreases as the fuel and oxidizer burn.
Thrust = (2.60 x 103 m/s)(1.50 x 104 kg/s)
Thrust = 3.9 x 107 N
Weight = m g = (3.0 x 106 kg)(9.8 m/s2)
Weight = 2.94 x 107 N
Fnet = Thrust - Weight
Fnet = (3.9 - 2.9) x 107 N = 1.0 x 107 N
F = m a
a = F / m = Fnet / m
a = (1.0 x 107 N)/(3 x 106 kg)
a = 3.33 m/s2
9.52 A large rocket with an exhaust speed of ve = 3 000 m/s develops a thrust of 24.0 million newtons (Thrust = 24.0 x 104 N).
(a) How much mass is being blasted out the rocket exhaust per second?
(b) What is the maximum speed the rocket can attain if it starts from rest in a force-free environment with ve = 3.00 km/s (or ve = 3 000 m/s) and if 90.0% of its initial mass is fuel and oxidizer?
As in the previous problem, from Eq 9.42 on p 279, we know
Thrust = | ve (dM/dt) |
(The absolute value bars are in this equation because (dM/dt) < 0 as the mass of the rocket decreases as the fuel and oxidizer burn.)
|dM/dt| = Thrust / ve
|dM/dt| = (24.0 x 104 N) / (3 000 m/s)
|dM/dt| = 80 kg/s
If we have done everything right, we know a mass flow rate must be measured in units of kg/s. But have we done everything right? Let's pause for a moment and check the units;
N / (m/s) = N - s / m
= [N - s / m][(kg-m/s2) / N]
= {(kg-m/s2) - s} / m
= (kg-m/s) / m
= kg / s
And that is exactly what we expected it to be!
Now for the maximum speed. From Eq 9.41, on p 278, we have (for vi = 0)
vf = ve ln [Mi/Mf]
Remember the exponential function ex (e = 2.7??????) and its inverse, the natural logrithm function ln(x) from your calculus class? They may have seemed strange but they show up as useful tools. We see them here, in rocket propulsion. And we will see them again (and again and again and again) in Thermodynamics (Newton's Law of Cooling) and in Electricity and Magnetism (charging a capacitor or current through a coil) and in Radioactivity (half-life is closely connected to exponential behavior).
If 90% of the initial mass is burned, then only one-tenth of the initial mass remains so that
Mi/Mf = 10
vf = (3 000 m/s) ln [10]
Solutions to the additional problems from Serway's fourth edition
We need the velocity of the superball immediately before and immediately after colliding with the floor. This part of the problem is just an old, standard kinematics problem
v2 = vo2 + 2 a (s - so) vbfr2 = 02 + 2 g (2.0 m)
vbfr2 = 2 (9.8 m/s2) (2.0 m)
vbfr2 = 39.2 m2/s2
vbfr = 6.26 m/s (down)
vaft2 = 2 (9.8 m/s2) (1.8 m)
vaft = 35.28 m2/s2
vaft= 5.94 m/s (up)
In calculating the momentum, this time we will take up as positive,
pbfr = m vbfr = (0.060 kg) ( - 6.26 m/s) = - 0.376 kg m/s paft = m vaft = (0.060 kg) ( + 5.94 m/s) = 0.356 kg m/s
(4ed) 9.2 Identical air cars (m = 200 g) are equipped with identical springs (k = 3 000 N/m). The cars move toward each other with speeds of 3.00 m/s on a horizontal air track and collide, compressing the springs (Fig P9.20) Find the maximum compression of each spring.
The initial kinetic energy of the moving air track cars is transferred to the springs as potential energy.Ei = (1/2) m1 v12 + (1/2) m2 v22 Ei = (1/2) (0.200 g) (3.00 m/s)2 + (1/2) (0.200 g) (3.00 m/s)2
Ei = 1.8 J
Ef = (1/2) k x12 + (1/2) k x22
By symmetry, the two springs compress the same amount; that is
x = x1 = x2 Ef = 2 [ (1/2) k x2 ]
Ef = Ei
2 [ (1/2) k x2 ] = 1.8 J
(3 000 N/m) x2 = 1.8 J
x2 = 6 x 10-4 m2
x = 0.024 m
x = 2.4 cm
(4ed) 9.3 Two blocks of mass m1 = 2.00 kg and m2 = 4.00 kg are released from a height of 5.00 m on a frictionless track as shown in Figure P9.40. The blocks undergo an elastic head-on collision.(a) Determine the two velocities just before the collision.
(b) Using Equations 9.20 and 9.21, determine the two velocities immediately after the collision.
(c) Determine the maximum height to which each block rises after the collision.
Each "falls" from the same height, 5.00 m. At the bottom of the track, each will have the same speed. We can find that speed from the conservation of energy.Ef = Ei Ef = (1/2) m v2 = m g h = Ei
v2 = 2 g h
v2 = 2 (9.8 m/s2) ( 5.0 m)
v2 = 98 m2/s2
v = 9.9 m/s
That is, the 2.0-kg block, m1, moves to the right with
v1 = + 9.9 m/s while the 4.0-kg block, m2, moves to the left with
v2 = - 9.9 m/s The total momentum of the two-block system before the collision is
PTot,i = pi1 + p2i PTot,i = (2.0 kg) (9.9 m/s) + (4.0 kg) ( - 9.9 m/s)
PTot,i = - 19.8 kg m/s
The masses are not the same so the momentum carried by each block is not the same, even tho' their speeds are the same. So the total momentum is not zero!
The two blocks undergo an elastic collision so their final velocities are given by Equations 9.20 and 9.21,
v1f = [(m1 - m2)/(m1 + m2)] v1i + [ 2 m2/(m1 + m2) ] v2i v1f = [(2 kg - 4 kg)/(2 kg + 4 kg)](9.9 m/s) + [ 2(4 kg)/(2 kg + 4 kg)]( - 9.9 m/s)
v1f = [(2 - 4)/(2 + 4)](9.9 m/s) + [ 2(4)/(2 + 4)]( - 9.9 m/s)
v1f = [(-2 / 6)](9.9 m/s) + [ 8 / 6]( - 9.9 m/s)
v1f = [(-10 / 6)](9.9 m/s)
v1f = - 16.5 m/s
Mass m1 moves to the left after the collision.
v2f = [2 m1 / (m1 + m2)] v1i + [ (m2 - m1) / (m1 + m2) ] v2i v2f = [2 (2 kg) / (2 kg + 4 kg)] (9.9 m/s) + [ (4kg - 2 kg) / (2 kg + 4 kg)] ( - 9.9 m/s)
v2f = [2 (2) / (2+ 4)] (9.9 m/s) + [ (4 - 2) / (2 + 4)] ( - 9.9 m/s)
v2f = [4 / 6] (9.9 m/s) + [2 / 6] ( - 9.9 m/s)
v2f = 3.3 m/s
Mass m2 moves to the right after the collision.
With these velocities, how high does each block rise? This is another conservation of energy question:
For block 1,
Eend = Eslide Eend = Uend = m g h1 = (1/2) m v1f2 = Kslide = Eslide
m g h1 = (1/2) m v1f2
h1 = [(1/2) v1f2] / g
h1 = [0.5(16.5 m/s)2] / (9.8 m/s2)
h1 = 13.9 m
For block 2,
Eend = Eslide Eend = Uend = m g h2 = (1/2) m v2f2 = Kslide = Eslide
m g h2 = (1/2) m v2f2
h2 = [(1/2) v2f2] / g
h2 = [0.5 (3.3 m/s)2] / (9.8 m/s2)
h2 = 0.55 m
As a check, we can calculate the final total energy of the system
Ef = U1 + U2 = m1 g h1 + m2 g h2 Ef = (2.0 kg) (9.8 m/s2) (13.9 m) + (4.0 kg) (9.8 m/s2) (0.55 m)
Ef = 272.4 J + 21.6 J
Ef = 294 J
What was the initial total energy of the sysetm?
Ef = U1 + U2 = m1 g h1 + m2 g h2 Ef = (2.0 kg) (9.8 m/s2) (5.0 m) + (4.0 kg) (9.8 m/s2) (5.0 m)
Ef = 98 J + 196 J
Ef = 294 J
Therefore, indeed, energy is conserved and we have confidence in our answer as well!
(4ed) 9.4 The separation between the hydrogen and chlorine atoms of the H Cl molecule is about 1.30 x 10-10 m. Determine the location of the center of mass of the molecule as measured from the hydrogen atom. Chlorine is 35 times more massive than hydrogen.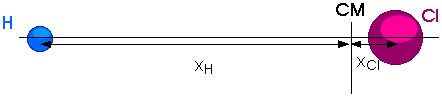
Measured from the Center of Mass, we have
mH x H = mCl x Cl m H x H = (35 mH) x Cl
x H = 35 x Cl
and we also know
xH+ xCl = 1.30 x 10-10 m so we can use
x H = 35 x Cl 36 x Cl = 1.30 x 10-10 m
x Cl = 3.61 x 10-12 m
x H = 1.26 x 10-10 m
And this is the distance of the Center of Mass from the hydrogen atom.
The mass of the square is just
Msq = Asq = (2 a)2
This mass of the square may be considered to be located at
Xsq = a Ysq = a
where we have established a coordinate system with its origin at the lower left corner of the piece of sheet metal.
The mass of the circle is
Mcir = - Acir r2 ]
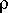
for our circle,
r = a/2 so that
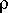
M cir = - [ This mass is effectively located at the center of the circle,
X cir = (3/2) a Y cir = (3/2) a
Now we can find the new location of the Center of Mass by
X = [ mi x i ] / [
X = [ Msq X sq + M cir X cir ] / [M sq + Mcir]
X = [( 4 a2
X = [( 4 a2 ) (a) + ( - [
X = [ 4 a3 - (
X = [ 4 a3 - 3/8
X = ( 4 - 3/8
X = ( 4 - 3/8
X = ( 4 - 3/8
X = (2.82 / 3.21) a
X = 0.88 a
And, by symmetery, we know Y = X or
Y = 0.88 a
(4ed) 9.6 A rocket engine consumes 80 kg of fuel per second. If the exhaust speed is 2.5 x 103 m/s, calculate the thrust of the rocket.From Equation 9.42, we knowThrust = vexh (dM/dt) Thrust = (2.5 x 103 m/s) (80 kg/s)
Thrust = 2.0 x 105 kg m/s2
Thrust = 2.0 x 105 N
(4ed) 9.7 A 3 000-kg rocket has 4 000 kg of fuel on board. The rocket is coasting through space at 100.0 m/s and needs to boost its speed to 300.0 m/s. It does this by firing its engines and ejecting fuel at a relative speed of 650.0 m/s until the desired speed is reached. How much fuel is left on board after this maneuver?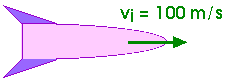
From Equation 9.41, we know
vf - vi = vexh ln [Mi / Mf] 300 m/s - 100 m/s = (650 m/s) ln [ 7 000 kg / Mf ]
The initial mass Mi of the rocket and the fuel is Mi = 7 000 kg.
200 = 650 ln [ 7 000 kg / M f ] ln [ 7 000 kg / M f ] = 200 / 650 = 0.308
7 000 kg / Mf = e0.308 = 1.36
M f = 7 000 kg / 1.36
M f = 5 147 kg
| Hmwk, Ch 8 | Homework Assignment Page | PHY 1350's Home Page | Hmwk, Ch 10 |
(c) Doug Davis, 2001; all rights reserved
