Ch 6, Circular Motion
Fc = m v2 / r
Homework
Ch 6, Circular Motion
Ch6: 7, 9, 19, 21, 24, 48, 51, 63, 67
Questions 4, 5, 6, 7, 8, 9
| Hmwk, Ch 5 | Homework Assignment Page | PHY 1350's Home Page | Hmwk, Ch 7 |
Additional problems from Serway's fourth edition
(4 ed) 6.1 An automobile moves at constant speed over the crest of a hill. The driver moves in a vertical circle of radius 18.0 m. At the top of the hill, she notices that she barely remains in contact with the seat. Find the speed of the vehicle.
(4 ed) 6.2 A car rounds a banked curve as in Figure 6.5. The radius of curvature of the road is R, the banking angle is
, and the coefficient of static friction is
.
(a) Determine the range of speeds the car can have without slipping up or down the road.
(b) Find the minimum value formu such that the minimum speed is zero.
(c) What is the range of speeds possible if R = 100 m,
Conceptual Questions
Q6.4 Why does mud fly off a rapidly turning automobile tire?For mud to move in a circle, there must be a (net) force on it -- directed toward the center of the circle. The value of that force is Fc = m v2/ r. As the velocity (or speed) increases, that force must increase if the piece of mud is to continue to move in a circle. As the velocity increases, the force that holds the mud to the wheel reaches its limit and the mud can no longer go around in a circle. When that limit is reached, the mud separates from the tire.
Q6.5 Imagine that you attach a heavy object to one end of a spring and then whirl the spring and object in a horizontal circle (by holding the free end of the spring). Does the spring stretch? If so, why? Discuss this in terms of the force causing the circular motion.
For the heavy object to move in a circle, there must be a (net) force on it, directed toward the center. That force is provided by the spring. For a spring to provide a force, it must be stretched.
Q6.6 It has been suggested that rotating cylinders about 16 km in length and 8 km in diameter be placed in space and used as colonies. The purpose of the rotation is to simulate gravity for the inhabitants. Explain this concept for producing an effective gravity.
To keep an inhabitant moving in a circle, the outside edge (or "floor") will have to exert a force, directed toward the center. This force is very much like the force that an ordinary floor exerts on a person so this would give the illusion of gravity.
Q6.7 Why does a pilot tend to black out when pulling out of a steep dive?
Coming out of a steep dive puts great great forces on everything -- including the pilot's blood. These forces -- often called "inertial forces" -- cause the pilot's blood to move from his brain to his lower body. If this happens enough -- for long enough or if the forces are great enough -- the brain is deprived of oxygen in the blood and the pilot blacks out.
This tends to happen when the forces are greater than about six times weight -- referred to as "six g's". Pressure suits can "squeeze" a pilot's legs and abdomane and keep the blood flowing to the brain. Some roller coasters get close enough to these conditions so that some victims -- er, I mean "guests" -- might black out. Some of these roller coasters pause for several seconds at the end to let blood get back to brains before letting the "guests" get off the coaster.
Q6.8 Describe a situation in which a car driver can have a centripetal acceleration but no tangential acceleration.
Uniform Circular Motion (UCM) is just such a situation. There will always be a centripetal acceleration in circular motion because of the changing direction. If the motion is uniform -- if the speed is constant -- there will be no tangential acceleration.
Q6.9 Describe the path of a moving object if its acceleration is constant in magnitude at all times and
(a) perpendicular to the velocity; and
This is Uniform Circular Motion (UCM).
(b) parallel to the velocity.
This is straight-line motion.
Problems from the current (5th) edition of Serway and Beichner.
6.7 While two astronauts were on the surface of the Moon, a third astronaut orbited the Moon. Assume the orbit to be circular and 100 km above the surface of the Moon. If the mass and radius of the Moon are 7.40 x 1022 kg and 1.70 x 106 m, determine
(a) the orbiting astronaut's acceleration,
(b) his orbital speed, and
(c) the period of the orbit.
The orbital radius is
r = 100 km + 1.70 x 106 m = 0.10 x 106 m + 1.70 x 106 m = 1.80 x 106 m
Fg = G M m / r2 = m ac
G M / r2 = a c
(6.672 x 10-11 N m2 / kg2 ) ( 7.40 x 1022 ) / ( 1.80 x 106 m)2 = a c
a c = 1.524 m / s2
a c = v2 / r
v2 = a c r = (1.524 m / s2) (1.80 x 106 m)
v2 = 2.743 x 106 m2 / s2
v = 1.656 x 103 m / s
v = D / t = C / t = 2 Î r / t
t = 2
r / v = 2
t = 6.829 x 103 s [ min / 60 s] [ h / 60 min ]
t = 1.897 h
6.9 A coin placed 30 cm from the center of a rotating horizontal turntable slips when its speed is 50 cm/s.
(a) What provides the force in the radial direction when before the coin slips?
(b) What is the coefficient of static friction between coin and turntable?
As always, don't start without good, clear diagrams. What are all the forces acting on the coin?
w is the weight, n is the "normal" force -- the force perpendicular to the surface -- and Ffr is the force of friction -- parallel to the surface. It is this friction force Ffr that provides the centeripetal force Fc.
Now, what is the coefficient of friction
Ffr =
n = w = mg
Ffr =
Ffr = Fc = m v2/r
Be careful with the units. We know v in cm/s and we know r in cm. We usually state g as 9.8 m/s2. If you just plug in the associated numbers the answer will be horrendous -- because the units are not the same. We can make a big deal of converting units or we can just use g as 980 cm/s2.
6.19 A pail of water is rotated in a vertical circle of radius 1.0 m. What must be the minimum speed of the pail at the top of the circle if no water is to spill out?
At the top of the circle, gravity pulls down -- toward the center of the circle -- with a force of w = m g. If the water is just on the verge of spilling out, this the only force on the water so that must also be the centripetal force.
Fc = m v2/r = m g = w
m v2/r = m g
v2/r = g
v2 = g r
v2 = (9.8 m/s2)(1.0 m)
v2 = 9.8 m2/s2
v = 3.13 m/s
6.21 A roller-coaster vehicle has a mass of 500 kg when fully loaded with passengers.
(a) If the vehicle has a speed of 20.0 m/s at point A, what is the force exerted by the track on the vehicle at this point?
(b) What is the maximum speed the vehicle can have at B and still remain on the track?
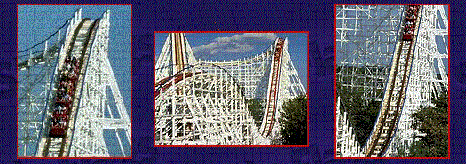
(a) If the vehicle has a speed of 20.0 m/s at point A, what is the force exerted by the track on the vehicle at this point?
The forces on mass m, the roller-coaster vehicle, are its weight mg pointing down and the force the track exerts Fn pointing up. Therefore, the net force Fnet is
Fnet = Fn - m g
This net force is the centrepital force Fc,
Fc = m v2 / r
Fnet = Fc
Fn - m g = m v2 / r
Fn = (m v2 / r) + m g
Fn = m [( v2 / r) + g ]
Fn =(500 kg) [( (20 m/s)2 / 10 m) + 9.8 m/s2 ]
Fn =(500 kg) [ 49.8 m/s2 ]
Fn = 24,900 N
That is about five times its weight of 5,000 N.
(b) What is the maximum speed the vehicle can have at B and still remain on the track?
To "still remain on the track" means the normal force Fn has just gone to zero, Fn = 0.
With the normal force equal to zero, there is only the weight mg available to supply the centripetal force Fc,
Fc = Fnet
m v2 / r = m g
v2 / r = g
v2 = g r = (9.8 m / s2 ) (15 m) = 147 m2 / s2
v = 12.12 m /s
6.24 A 5.00-kg mass attached to a spring scale rests on a frictionless, horizontal surface as in Figure P6.26. The spring scale, attached to the front end of a boxcar, reads 18.0 N when the car is in motion.(a) If the spring scale reads zero when the car is at rest, determine the acceleration of the car while it is in motion.
(b) What will the spring scale read if the car moves with constant velocity?
(c) Describe the forces on the mass as observed by someone in the car and by someone at rest, outside the car.
(a) If the spring scale reads zero when the car is at rest, determine the acceleration of the car while it is in motion.
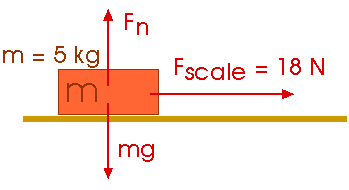
Fnet = Fscale = 18 N = (5 kg) a = ma
a = 18 N / 5 kg
a = 3.6 m / s2
(b) What will the spring scale read if the car moves with constant velocity?
At constant velocity, the net force on the block must be zero. Only the scale exerts a horizontal force on the block so it must read zero.
(c) Describe the forces on the mass as observed by someone in the car and by someone at rest, outside the car.
An observer at rest, on the outside sees the spring scale exerting a force to the right which causes the block to accelerate to the right. The force of the spring scale is the only horizontal force on the block and it is the net force which causes the block to accelerate.
An observer riding along with the block inside the car sees the block at rest in her reference frame. The spring scale exerts a force to the right but the block remains at rest. Therefore, our ride-along observer will conclude that there is an additional force to the left acting on the block. We call this an "inertial force" or a "ficticious force" due to the acceleration of the reference frame.
6.48 In a hydrogen atom, the electron in orbit around the proton feels an attractive force of about 8.20 x 10-8 N. If the radius of the "orbit" is 5.30 x 10-11 m, what is the frequency in revolutions per second?
Fc = m v2 / r
v2 = Fc r / m = ( 8.20 x 10-8 N)(5.30 x 10-11 m) / (1.67 x 10-27 kg)
v2 = 2.60 x 109 m2 / s2
v = 5.101 x 104 m/s
v = r
= v / r = (5.101 x 104 m/s) / ( 5.30 x 10-11 m) = 9.625 x 1014 rad / sec
f = 9.625 x 1014 rad / sec [ rev / 2
f = 1.532 x 1014 rev / sec
6.51 An air puck of mass 0.25 kg is tied to a string and allowed to revolve in a circle of radius 1.0 m on a frictionless, horizontal table. The other end of the string passes through a hole in the center of the table and a mass of 1.0 kg is tied to it (Fig P6.38). The suspended mass remains in equilibrium while the puck on the tabletop revolves. What are
(a) the tension in the string,
(b) the central force exerted on the puck, and
(c) the speed of the puck?
What are (a) the tension in the string,
Look at the forces on the hanging mass. From those you can readily see that the tension in the string must equal the weight of the hanging mass,
T = m2 g
T = (1.0 kg) ((9.8 m/s2)
T = 9.8 N
(b) the central force exerted on the puck, and
The only horizontal force acting on the puck is the tension in the string so this tension is the central force and is equal to the centripetal force,
Fc = T = m2 g
Fc = T = 9.8 N
(c) the speed of the puck?
Fc = m1 v2 / R = m2 g
(0.25 kg) v2 / 1.0 m = 9.8 N
v2 = (m2 / m1) g R
v2 = (9.8 / 0.25) m2 / s2 = 39.2 m2 / s2
v = SQRT [ (m2 / m1) g R ]
v = 6.26 m / s
6.63 An amusement park ride consists of a large vertical cylinder that spins about its axis fast enough that any person inside is held up against the wall when the floor drops away (Fig P6.49). The coefficient of static friction between the person and the wall is
Six Flags - St Louis - calls this ride "Tom's Twister". Midways at fairs often have one like this called "the Rotor". Another variation, often called "the Round-Up" tilts victims -- I mean guests -- up at an angle. Look for them.
(a) Show that the maximum period of revolution necessary to keep the person from falling is T = (4
Fx = - Fn = - m v2 / R = - Fc
Fn = m v2 / R
Ff = m g
Ff =
Ff =
v = C / T = 2
v2 = 4
T2 =
T = [
(b) Obtain a numerical value fo T if R = 4.00 m and
T = [
T = [(0.4)(4
T = 2.5 s
(c) How many revolutions per minute does the cylinder make?
f = 1 / T = (1 rev) / (2.5 s) [ 60 s / min ] = 24 rev / min
f = 24 rpm
Solutions to additional problems from Serway's fourth edition.
(4 ed) 6.1 An automobile moves at constant speed over the crest of a hill. The driver moves in a vertical circle of radius 18.0 m. At the top of the hill, she notices that she barely remains in contact with the seat. Find the speed of the vehicle.
Since the driver "barely remains in contact with the seat", the normal force Fn, between here and the seat, is zero. She moves in a circle, so the net force on her must provide the centripetal force and the only force available is her weight, mg.
Fc = m v2 / r
Fc = m g
m v2 / r = m g
v2 / r = g
v2 = g r = ( 9.8 m/s2 ) ( 18 m ) = 176.r m2 / s2
v = 13.28 m / s
(4 ed) 6.2 A car rounds a banked curve as in Figure 6.5. The radius of curvature of the road is R, the banking angle is
(a) Determine the range of speeds the car can have without slipping up or down the road.
(b) Find the minimum value formu such that the minimum speed is zero.
(c) What is the range of speeds possible if R = 100 m,
First, a note of caution. It is very easy -- almost "automatic" -- to choose x- and y-axes like this,
with the x-axis along the plane. But don't do that here! The centripetal force and acceleration will be directed toward the center of the circle. And the center of the circle does not lie along this x-axis. Rather, choose the x-axis so the center of the circle does lie on it.
Now, with these axes, the net force in the y-direction will be zero, Fnet,y = 0 and the net force in the x-direction will be the centripetal force, Fnet,x = - Fc = - m v2 / r
Friction always opposes the motion so we must look at two possibilities for the friction force. We must use separate free-body diagrams for the two cases
when the car is about to slide "up" the bank
when the car is about to slide "down" the bank
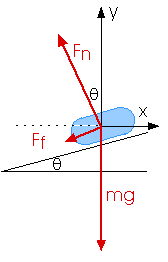
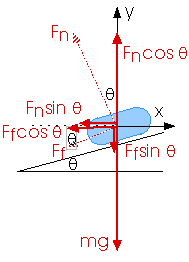
Fnet,y = 0
Fn cos
Fn cos
Fn(cos
Fn = m g / (cos
Fnet,x = - Fc = - m v2 / r
Fnet,x = - Fn sin
m v2 / r = Fn sin
m v2 / r = Fn sin
m v2 / r = Fn (sin
v2 = Fn (sin
v2 = [1 / (cos
v2 = [1/(cos
v2 = [sin
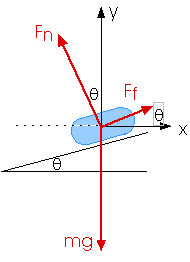
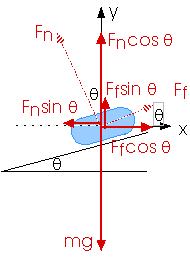
Fnet,y = 0
Fn cos
Fn cos
Fn(cos
Fn = m g / (cos
Fnet,x = - Fc = - m v2 / r
Fnet,x = - Fn sin
m v2 / r = Fn sin
m v2 / r = Fn sin
m v2 / r = Fn (sin
v2 = Fn (sin
v2 = [1 / (cos
v2 = [1/(cos
v2 = [sin
(c) Now, with specific numerical values, this is
v2 = {[sin 10o + 0.10 cos 10o]/[cos 10o - 0.10 sin 10o]}(100 m)(9.8 m/s2)
v2 = {[0.174 + 0.10 (0.985)]/[0.985 - 0.10 (0.174)]}(100 m)(9.8 m/s2)
v2 = {[0.174 + 0.099]/[0.985 - 0.0174]}(100 m)(9.8 m/s2)
v2 = {[0.272]/[0.968]}(980 m2/s2)
v2 = 275 m2/s2
v = 16.6 m/s
This is the maximum speed.
(c) Now, with specific numerical values, this is
v2 = {[sin 10o - 0.10 cos 10o]/[cos 10o + 0.10 sin 10o]}(100 m)(9.8 m/s2)
v2 = {[0.174 - 0.10 (0.985)]/[0.985 + 0.10 (0.174)]}(100 m)(9.8 m/s2)
v2 = {[0.174 - 0.099]/[0.985 + 0.0174]}(100 m)(9.8 m/s2)
v2 = {[0.075]/[1.002]}(980 m2/s2)
v2 = 73.3 m2/s2
v = 8.6 m/s
This is the minimum speed.
(a) Determine the range of speeds the car can have without slipping up or down the road.
(b) Find the minimum value for
We can set v = 0. Actually, it is easier to set v2 = 0
v2 = [sin
sin
sin
(c) What is the range of speeds possible if R = 100 m,
These values are at the end of the table above.
| Hmwk, Ch 5 | Homework Assignment Page | PHY 1350's Home Page | Hmwk, Ch 7 |
(c) Doug Davis, 2001; all rights reserved
