

Ch 7, Work and Energy Homework: Ch7; 2, 6, 11, 20, 21, 28, 40, 45, 52, 53
Questions 4, 5, 9, 12, 14

Additional problems from Serway's fourth edition
(4 ed) 7.1 A cheerleader lifts his 50.0-kg partner straight up off the ground a distance of 0.60 m before releasing her. If he does this 20 times, how much work has he done?
(4 ed) 7.2 If you push a 40.0-kg crate at a constant speed of 1.40 m/s across a horizontal floor (k = 0.25), at what rate
(a) is work being done on the crate by you and
(b) is energy dissipated by the frictional force?
(4 ed) 7.3 A block of mass m hangs on the end of a cord and is connected to a block of mass M by the pulley arrangement shown in Figure P7.41. Using energy considerations,(a) find an expression for the speed of m as a function of the distance it has fallen. Assume that the blocks are initially at rest and there is no friction.
(b) Repeat (a) assuming sliding friction (
k) between mass M and the table.
(c) Show that the result obtained in (b) reduces to that obtained in (a) in the limit as
k goes to zero.
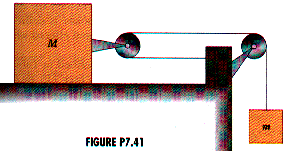
(4 ed) 7.4 A block of mass 0.60 kg slides 6.0 m down a frictionless ramp inclined at 20o to the horizontal. It then travels on a rough horizontal surface wherek = 0.50.
(a) What is the speed of the block at the end of the incline?
(b) What is its speed after traveling 1.00 m on the rough surface?
(c) What distance does it travel on this horizontal surface before stopping?
(4 ed) 7.5 A time-varying net force acting on a 4.0-kg particle causes the particle to have a displacement given byx = 2.0 t - 3.0 t2 + 1.0 t3,
where x is in meters and t is in seconds. Find the work done on the particle in the first 3.0 s of motion.
(4 ed) 7.6 A 1,500-kg car accelerates uniformly from rest to 10 m/s in 3.0 s.Find (a) the work done on the car in this time,
and (b) the average power delivered by the engine in the first 3.0 s,
and (c) the instantaneous power delivered by the engine at t = 2.0 s.
(4 ed) 7.7 A car of weight 2,500 N operating at a rate of 130 kW develops a maximum speed of 31 m/s on a level, horizontal road. Assuming that the resistive force (due to friction and air resistance) remains constant.(a) What is the car's maximum speed on an incline of 1 in 20 (ie, if theta is the angle of the incline with the horizontal, sin
= 1/20)?
(b) What is its power output on a 1-in-10 incline if the car is traveling at 10 m/s?

 Conceptual Questions
Conceptual Questions
Q7.4 Can the kinetic energy of an object be negative?
No. Kinetic energy is given by KE = (1/2) m v2. The mass m is always positive and v2 is positive so KE must always be positive (of course, if v = 0 then KE = 0). KE can not be negative.
Q7.5 (a) If the speed of a particle is doubled, what happens to its kinetic energy?KE = (1/2) m v2 so doubling the speed v means the Kinetic Energy is increased fourfold.
(b) if the net work done on a particle is zero, what can be said about the speed?
The net work done on a particle is equal to the change in its Kinetic Energy. So if the net work is zero the Kinetic Energy remains constant and that means the speed, too, remains constant.
Q7.9 When a punter kicks a football, is he doing any work on the ball while his toe is in contact with it?Yes, a force is being exerted on the ball as it moves through a distance. That's the definition of work.
Is he doing any work on the ball after it loses contact with his toe?
No, once his toe looses contact with the ball, the force his toe exerts is zero.
Are any forces doing work on the ball while it is in flight?
Yes, gravity and air resistance continue to do work on the ball.
Q7.12 As a simple pendulum swings back and forth, the forces acting on the suspended mass are the force of gravity, the tension in the supporting cord, and air resistance.(a) Which of these forces, if any, does no work on the pendulum?
The force in the supporting cord is perpendicular to the motion so that force does no work.
(b) Which of thee forces does negative work at all times during its motion?
Air resistance -- like all friction forces -- always does negative work.
(c) Describe the work done by the force of gravity while the pendulum is swinging.
The force of gravity does positive work as the pendulum "falls" from either extreme to its lowest position; this causes the pendulum to speed up. The force of gravity does negative work as the pendulum "rises" from its lowest position to either extreme; this causes the pendulum to slow down.
Q7.14 An older model car accelerates from 0 to a speed v in 10 s. A newer, more powerful sports car accelerates from 0 to 2 v in the same time period. What is the ratio of powers expended by the two cars?Assume the two cars have the same mass.
The car going 2 v has four times the Kinetic Energy. If it acquired this much energy in the same time, then the power supplied to it is also four times as much.
 Problems from the current (5th) edition of Serway and Beichner
Problems from the current (5th) edition of Serway and Beichner
7.2 A shopper in a supermarket pushes a cart with a force of 35 N directed at an angle of 25o downward from the horizontal. Find the work done by the shopper as she moves down an aisle 50 m in length.
W = F d cos
W = (35 N)(50 m) cos 25o
W = (35 N)(50 m)(0.906)
W = 1 586 N-m = 1 586 J
It is entirely equivalent to think of this as
W = Fx d
W = [(35 m) cos 25o] (50 m)
W = 1 586 J
7.6 A 15.0-kg block is dragges over a rough, horizontal surface by a 70.0-N force acting at 20o above the horizontal. The block is displaced 5.0 m and the coefficient of kinetic friction is 0.30. Find the work done by(a) the 70-N force,
(b) the normal force, and
(c) the force of gravity.
(d) What is the energy loss due to friction?
W = F d cos
W70 = Fext d cos 20o
W70 = (70 N)(5 m)(0.9397)
W70 = 328.9 J
Wn = n d cos 90o
Wn = 0
Wg = w d cos 90o
Wg = 0
Wfr = Ffr d cos 180o
What is the force of friction Ffr? We do know that
Ffr = 0.30 n
But what is the normal force n? We see enough special cases when n = w = mg that one can intuitively jump to the wrong conclusion and thing that n = w = mg all the time. That is not the case in general and that is not the case here. The block is not jumping up off the plane and it is not burrowing down into the plane. Therefore, the sum of the forces in the vertical direction must be zero.
Fnet,y = n + Fext,y - w = 0
n + (70 N)(sin 20o) - (15 kg)(9.8 m/s2) = 0
n + (70 N)(0.342) - (15)(9.8) N = 0
n + 23.9 N - 147 N = 0
n - 123.1 N = 0
n = 123.1 N
With the value of the normal force n now known, we can calculate the friction force Ffr.
Ffr = 0.30 n
Ffr = 0.30 (123.1 N)
Ffr = 36.9 N
Now we can calculate the work done by the friction force,
Wfr = Ffr d cos 180o
Wfr = - (36.9 N)(5.0 m)
Wfr = - 184.6 J
What does the negative sign mean. The force of friction decreases the energy. This is the energy loss which shows up as heat.
7.11 A force F = (6i - 2j) N acts on a particle that undergoes a displacement d = (3i + j) m.Find (a) the work done by the force on the particle
and (b) the angle between F and d.
W = F
d
W = [(6i - 2j) N]
[(3i + j) m]
W = [(6i - 2j)
(3i + j)] (N-m)
W = [(6i - 2j)
(3i + j)] J
There are (at least) two ways we can evaluate this dot-product.
W = [(6i)
(3i) + (6i)
(j) - (2j)
(3i) - (2j)
(j)] J
W = [(6)(3)(i
i) + (6)(1)(i
j) - (2)(3)(j
i) - (2)(1)(j
j)] J
W = [(6)(3)(1) + (6)(1)(0) - (2)(3)(0) - (2)(1)(1)] J
W = [18 + 0 - 0 - 2] J
W = 16 J
An alternative is to remember the dot product in terms of components as
A
B = Ax Bx + Ay By
Then the work can be written as
W = F
d = Fx dx + Fy dy
W = F
d = [(6)(3) + ( - 2)(1)] N-m
W = F
d = [18 - 2] J
W = 16 J
7.20 An archer pulls her bow string back 0.400 m by exerting a force that increases uniformly from zero to 230 N.(a) What is the equivalent spring constant of the bow?
(b) How much work is done in pulling the bow?
F = k x230 N = k (0.4 m)
k = 230 N / 0.4 m
k = 575 N/m
W = (1/2) k x2
W = (1/2) (575 N/m) (0.4 m)2
W = 46 J
7.21 A 6,000-kg freight car rolls along rails with negligible friction. The car is brought to rest by a combination of two coiled springs, as illustrated in Figure P7.21. Both springs obey Hooke's law, with k1 = 1600 N/m and k2 = 3400 N/m. After the first spring compresses a distance of 30.0 cm, the second spring (acting with the first) increases the force so that there is additional compression as shown in the graph. If the car is brought to rest 50.0 cm after first contacting the two-spring system, find the car's initial speed.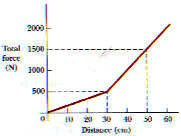 The wording of this question may be ambiguous. When it asks "If the car is brought to rest 50.0 cm after first contacting the two-spring system, find the car's initial speed." -- exactly what is meant by "after first contacting the two-spring system"? This solution takes "after first contacting the two-spring system" to mean the car moves 50.0 cm after first contacting the first spring, with k1 = 1600 N/m.
The wording of this question may be ambiguous. When it asks "If the car is brought to rest 50.0 cm after first contacting the two-spring system, find the car's initial speed." -- exactly what is meant by "after first contacting the two-spring system"? This solution takes "after first contacting the two-spring system" to mean the car moves 50.0 cm after first contacting the first spring, with k1 = 1600 N/m.The first spring is compressed the full distance of x1 = 0.50 m so it does work of
W1 = ( 1/2 ) k1 x12 = 0.5 (1 600 N/m) (0.5 m)2 = 200 J
The second spring is compressed only after the freight car moves a distance of 0.30 m, so it is only compressed a distance of x2 = 0.20 m so it does work of
W2 = ( 1/2 ) k2 x22 = 0.5 (3 400 N/m) (0.2 m)2 = 68 J
So both springs have done a total amount of work of
WTot = W1 + W2 = 200 J + 68 J = 268 J
[ There is an alternate way to do this. We could figure the work done during the first 0.30 m with k = 1600 N/m and then find the work done during the last 0.20 m from the "area" under the graph. The total amount of work should be the same, either way ].
Actually, this total work is negative that amount, WTot = - 268 J, since the force and displacement are in opposite direction. This has changed the freight car's Kinetic Energy from its initial value of
KEi= ( 1/2 ) m vi2
to its final value of zero. That is
KEi= ( 1/2 ) m vi2 = ( 1/2 ) (6 000 kg) vi2 = 268 J = Wsprings
vi2 = 0.089 m2 / s2
vi = 0.30 m/s
7.28 A 0.30-kg ball has a speed of 15.0 m/s.(a) What is its kinetic energy?
(b) If its speed were doubled, what would be its kinetic energy?
KE = (1/2) m v2
KE = (1/2) (0.30 kg) (15.0 m/s)2
KE = 33.75 J
Since the speed is squared, doubling the speed will increase the KE by a factor of four.
KEdbl = 4 KEorig
KEdbl = 135 J
7.40 An Atwood's machine has a 3.00 kg mass and a 2.00-kg mass at ends of the string (as in Figure 5.15). The 2.00-kg mass is released from rest on the floor, 4.00 m below the 3.00-kg mass.(a) If the pulley is frictionless, what will be the speed of the masses when they pass each other?
(b) Suppose that the pulley does not rotate and the string must slide over it. If the total frictional force between the pulley and the string is 4.00 N, what are their speeds when the masses pass each other?
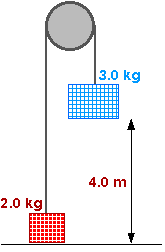 Wnet =
Wnet =KE
Wnet = W2 + W3 = - (2 kg) (9.8 m/s2) (2 m) + (3 kg) (9.8 m/s2) (2 m)
Wnet = 19.6 J
The w's in the diagram -- w2 and w3 -- are the weights;
w2 = m2 g = (2.0 kg) (9.8 m/s2)
w3 = m3 g = (2.0 kg) (9.8 m/s2)
The capital W's in the equation above -- W2 and W3 -- are the amounts of work done on the 2.0-kg mass and the 3.0-kg mass by gravity.
Only the force of gravity does work on "the system". We need not -- can not -- consider the tension in the cord for that is an "internal force" just like the forces that hold the blocks together.
The blocks have a common velocity v,
KE = 0.5 (2.0 kg) v2 + 0.5 (3.0 kg) v2 = (2.5 kg) v2
KE = (2.5 kg) v2 = 19.6 J = Wnet
v2 = 7.84 m2 / s2
v = 2.8 m / s
Now, consider friction.
Wf = - (5.0 N) (2.0 m) = - 10 J
Wnet = 19.6 J - 10 J = 9.6 J
KE = (2.5 kg) v2 = 9.6 J = Wnet
v2 = 3.84 m2 / s2
v = 1.96 m /s
7.45 A certain automobile engine delivers 2.24 x 104 W (or 22.4 kW or 30 hp) to its wheels when moving at a constant speed of 27.0 m/s (about 60 mi/h or about 100 km/h). What is the resistive force acting on the automobile at that speed?P = F v
F = P / v
F = [2.24 x 104 W]/[27 m/s]
F = 830 N
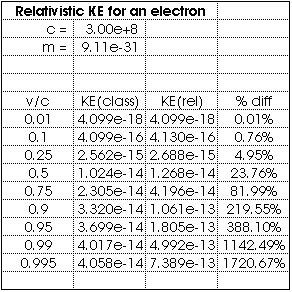
7.52 An electron moves with a speed of 0.995 c.(a) What is its kinetic energy?
(b) If you use the classical expression to calculate its kinetic energy, what percentage error would result?
It is fun to look at more than just v = 0.995 c. Repetitive calculations are often easiest to do with a simple spreadsheet.
7.53 A proton in a high-energy accelerator moves with a speed of c/2. Using the work-energy theorem, find the work required to increase its speed to(a) 0.750 c and
(b) 0.995 c.
For common, ordinary speeds, we found that the (kinetic) energy of a particle with mass m and speed v is KE = (1/2) m v2. But for very high speeds -- for speeds close to that of light -- we had to modify that and use
E = m c2
m = mo / SQRT(1 - v2/c2)
Eo = mo c2
KE = E - Eo
KE = mo c2 [ {1/SQRT(1 - v2/c2)} - 1]
This does not look very much like KE = (1/2) m v2 ! So it is worth reminding ourselves tha this unusual looking expression does, indeed, reduce to KE = (1/2) m v2 for v << c !
First, let's find the "rest energy" of the proton since this factor appears in all our future calculations.
Eo = mo c2
Eo = (1.672 x 10 - 27 kg)(3 x 108 m/s)2
Eo = 5.016 x 10 - 11 J
This is perfectly okay as it is. However, instead of dealing with such small numbers, it is customary to talk about these energies in units of MeV -- millions of electron-Volts. We will explore MeV's more in PHY 1360 (next semester). For the present, we can simply pull out of the air the appropriate conversion factor,
1 eV = 1.6 x 10 - 19 J1 MeV = 1.6 x 10 - 16 J
Therefore,
Eo = 5.016 x 10 - 11 J [1 MeV / 1.6 x 10 - 16 J]
Eo = 313 500 Mev
Eo = 313.5 Gev
One GeV is one giggaelectron-volt. Gigga means "billion" or 109.
E = m c2
m = mo / SQRT(1 - v2/c2)
Eorig = [mo / SQRT(1 - vorig2/c2)] c2
Eorig = [mo c2][1/ SQRT(1 - vorig2/c2)]
Eorig = [313.5 Gev][1/ SQRT(1 - {0.50 c}2/c2)]
Eorig = [313.5 Gev][1/ SQRT(1 - {0.50}2)]
Eorig = [313.5 Gev][1/ SQRT(1 - 0.25)]
Eorig = [313.5 Gev][1/ SQRT(0.75)]
Eorig = [313.5 Gev][1/ 0.866]
Eorig = [313.5 Gev][1.155]
Eorig = 362 Gev
That's the total energy -- KE plus "rest mass energy" -- that the proton has originally. Now, how much energy does it have for the speeds given in question (a) and question (b)?
Ea = [mo / SQRT(1 - va2/c2)] c2
Ea = [mo c2][1/ SQRT(1 - va2/c2)]
Ea = [313.5 Gev][1/ SQRT(1 - {0.750 c}2/c2)]
Ea = [313.5 Gev][1/ SQRT(1 - {0.750}2)]
Ea = [313.5 Gev][1/ SQRT(1 - 0.5625)]
Ea = [313.5 Gev][1/ SQRT(0.4375)]
Ea = 313.5 Gev][1/ 0.661]
Ea = [313.5 Gev][1.512}
Ea = 474 GeV
How much energy do we need to add to go from the original speed (vorig = 0.500 c) tho this speed (va = 0.75 c)?
Ea = Ea - Eorig
Ea = (474 - 362) GeV
Ea = 112 GeV
Now we do exactly the same thing for vb = 0.995 c.
Eb = [mo / SQRT(1 - vb2/c2)] c2
Eb = [mo c2][1/ SQRT(1 - vb2/c2)]
Eb = [313.5 Gev][1/ SQRT(1 - {0.995 c}2/c2)]
Eb = [313.5 Gev][1/ SQRT(1 - {0.995}2)]
Eb = [313.5 Gev][1/ SQRT(1 - 0.990025)]
Eb = [313.5 Gev][1/ SQRT(0.009975)]
Eb = [313.5 Gev][1/ 0.09987]
Eb = [313.5 Gev][10.012]
Eb = 3 139 GeV
How much energy do we need to add to go from the original speed (vorig = 0.500 c) tho this speed (vb = 0.995 c)?
Eb = Eb - Eorig
Eb = (3 139 - 362) GeV
Eb = 2 777 GeV
Solutions to the additional problems from Serway's fourth edition.
(4 ed) 7.1 A cheerleader lifts his 50.0-kg partner straight up off the ground a distance of 0.60 m before releasing her. If he does this 20 times, how much work has he done?w = mg = (50 kg) (9.8 m/s2) = 490 NW = F s = (490 N) (0.60 m) = 294 N-m = 294 J
WTot = 20 x W = (20) (290 J) = 5,880 J
WTot = 5,880 J
(4 ed) 7.2 If you push a 40.0-kg crate at a constant speed of 1.40 m/s across a horizontal floor (k = 0.25), at what rate
(a) is work being done on the crate by you and
(b) is energy dissipated by the frictional force?
P = F vWe must find the horizontal force F
From the diagram, we find that
F = Ff
Fn = m g = (40 kg) (9.8 m/s2) = 392 N
Ff =
Fn = (0.25) (392 N) = 98 N
F = 98 N
P = F v = (98 N) (1.4 m/s) = 137 N-m / s = 137 J / s = 137 W
The friction force Ff dissipates energy at the same rate,
P = 137 W
(4 ed) 7.3 A block of mass m hangs on the end of a cord and is connected to a block of mass M by the pulley arrangement shown in Figure P7.41. Using energy considerations,(a) find an expression for the speed of m as a function of the distance it has fallen. Assume that the blocks are initially at rest and there is no friction.
(b) Repeat (a) assuming sliding friction (
k) between mass M and the table.
(c) Show that the result obtained in (b) reduces to that obtained in (a) in the limit as
k goes to zero.
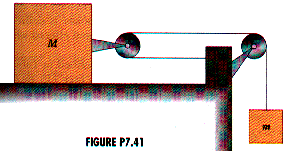 When hanging mass m moves a distance x, the sliding mass M moves only half that distance, x/2. When hanging mass m has speed v, sliding mass M has a speed of only half that, v/2.
When hanging mass m moves a distance x, the sliding mass M moves only half that distance, x/2. When hanging mass m has speed v, sliding mass M has a speed of only half that, v/2.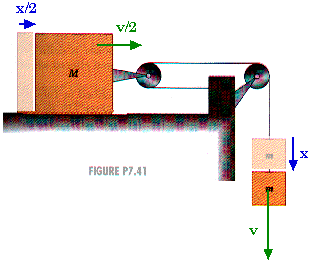
When the hanging mass has moved a distance x from its initial position, the force of gravity has done work of
Wg = m g x
That is the only work that is done on the "system" since the forces on sliding mass M -- the force of gravity and the normal force of the table -- are perpendicular to the displacement. The tension in the cord is an "internal force" and does not act on the "system" from the outside. This work due to gravity is the net work so it must equal the change in KE of the "system"
Wg = Wnet = m g x =
KE = KE - KEi = KE - 0 = KE = KEM + KEm
m g x = (1/2) M (1/2 v )2 + (1/2) m v2
m g x = 1/8 M v2 + (1/2) m v2
m g x = (1/2) [ 1/4 M + m ] v2
v2 = 2 m g x / [ 1/4 M + m ]
v2 = { 2 m g / [ 1/4 M + m ] } x
This is without friction.
Now, go back and add in friction. With friction present, the friction force is
Ff =
FN =
M g
As hanging mass m moves distance x, the sliding mass M moves a distance x/2 and work due to the friction force is done on it in the amount of
Wf = - Ff (x/2) = -
M g x /2
That means the net work is
Wnet = Wg + Wf = m g x -
M g x /2
Wnet = m g x -
M g x /2 =
KE = KE - KEi = KE - 0 = KE = KEM + KEm
m g x -
M g x /2 = KEM + KEm
m g x -
M g x /2 = KEM + KEm = (1/2) M (1/2 v )2 + (1/2) m v2
[ m -
M / 2 ] g x = (1/2) [ (1/4) M + m ] v2
v2 = 2 { [ m -
M / 2 ] / [ (1/4) M + m ] } g x
Does this expression reduce to our earlier, frictionless expression (as it must) when the coefficient of friction is zero? Set
= 0 and see;
v2 = 2 { [ m -
M / 2 ] / [ (1/4) M + m ] } g x
v2 = 2 { [ m - (0) M / 2 ] / [ (1/4) M + m ] } g x
v2 = 2 { [ m ] / [ (1/4) M + m ] } g x
v2 = 2 { [ m ] / [ (1/4) M + m ] } g x
And, indeed, this is the same expression as we got for the frictionless case directly.
(4 ed) 7.4 A block of mass 0.60 kg slides 6.0 m down a frictionless ramp inclined at 20o to the horizontal. It then travels on a rough horizontal surface wherek = 0.50.
(a) What is the speed of the block at the end of the incline?
(b) What is its speed after traveling 1.00 m on the rough surface?
(c) What distance does it travel on this horizontal surface before stopping?
(a) What is the speed of the block at the end of the incline?
On the frictionless incline, the normal force does no work, Wn= 0. Only the force of gravity does any work,Wg = F s cos
= ( m g ) (6.0 m) cos 70o = (0.60 kg) (9.8 m/s2) (6.0 m) (0.342) = 12.1 J
Wg = 12.1 J
Notice that this has the cosine of 70o rather than of 20o. In writing W = F s cos
, the angle
is the angle between the force and the displacement.
Wnet = Wg + Wn = 12.1 J
Wnet =
KE = KE - KEi = KE
Wnet = (1/2) m v2
(1/2) m v2 = (1/2) (0.60 kg) v2 = 12.1 J
v2 = 40.22 m2 / s2
v = 6.34 m / s
This is the speed at the bottom of the incline and the beginning of the rough horizontal plane that has friction.
From the force diagram, you can see that
Fn = m g = (0.60 kg) (9.8 m/s2) = 5.88 N
Ff =
Fn = (0.5) (5.88 N) = 2.94 N, pointing to the left
Along this rough, horizontal plane, only this friction force Ff does any work. By the time the block has moved a distance of 1.0 m along the plane, the net work done on the block is
Wnet= Wf = - (2.94 N) (1 m) = - 2.94 J
Wnet =
KE = KE1.0 m - KEo = KE1.0 m - 12.1 J = - 2.9 J
KE1.0 m = 12.1 J - 2.9 J = 9.2 J
KE1.0 m = 9.2 J = (1/2) m v2 = (1/2) (0.60 kg) v2
v2 = 30.7 m2 / s2
v = 5.5 m / s
Now, how far does it travel before it completely stops. At that point, KEf = 0. The work done by friction in moving this distance X is
Wnet= Wf = - (2.94 N) ( Xf )
And this is just equal to the change in KE, from its initial value of 12.1 J at the bottom of the inclined plane until it goes to zero,
- (2.94 N) X f = - 12.1 J
X f = 4.11 m
(4 ed) 7.5 A time-varying net force acting on a 4.0-kg particle causes the particle to have a displacement given byx = 2.0 t - 3.0 t2 + 1.0 t3,
where x is in meters and t is in seconds. Find the work done on the particle in the first 3.0 s of motion.
We need the change in KE so we need KE at t = 0 and KE at t = 3.0 sv = dx/dt = 2.0 t0 - 3.0 ( 2 t ) + 1.0 (3 t2 ) = 2.0 - 6.0 t + 3.0 t2
vo = v(t = 0) = 2.0 m/s
vf = v(t = 3 s) = 2 - 6(3) + 3(32) = 2 - 18 + 27 = 11 m/s
KEo = (1/2) m vo2 = (1/2) (4.0 kg) (2 m/s)2 = 8 J
KEf = (1/2) m vv2 = (1/2) (4.0 kg) (11 m/s)2 = 242 J
Wnet =
KE = 234 J
(4 ed) 7.6 A 1,500-kg car accelerates uniformly from rest to 10 m/s in 3.0 s.Find (a) the work done on the car in this time,
and (b) the average power delivered by the engine in the first 3.0 s,
and (c) the instantaneous power delivered by the engine at t = 2.0 s.
Wnet =
KE = 0.5 (1 500 kg) (10 m/s)2 = 75 000 J = 75 kJ
Pavg = W / t = 75 kJ / 3 s = 25 kW = 25 000 W
For t = 2 s,
P = F v
F = m a = m (
v /
t) = [1 500 kg] [(10 m/s) / 3 s] = 5 000 N = 5 kN
a =
v /
t = (10 m/s) / 3 s = 3.33 m / s2
v = vi + a t = 0 + ( 3.33 m / s2) (2 s) = 6.67 m / s
P = (5 000 N) (6.67 m / s)
P = 33 350 W = 33.35 kW
(4 ed) 7.7 A car of weight 2,500 N operating at a rate of 130 kW develops a maximum speed of 31 m/s on a level, horizontal road. Assuming that the resistive force (due to friction and air resistance) remains constant.(a) What is the car's maximum speed on an incline of 1 in 20 (ie, if theta is the angle of the incline with the horizontal, sin
= 1/20)?
(b) What is its power output on a 1-in-10 incline if the car is traveling at 10 m/s?

We know the power can be calculated from
P = F v
Since the car is not accelerating, the force F supplied by the engine is just equal to the resistive forces that retard its forward motion.
F = P / v = (130 000 W) / (31 m/s) = 4 194 N = 4.194 kN
This is the resistive force which we will assume to stay at this value.
Now, climb a hill with a 1-in-20 incline.
On this hill, in addition to the resistive force of 4 194 N, there is also a component of the weight that points "down" the hill; let's call this force F||,
F|| = w sin
= (2 500 N) (1 / 20) = 125 N
Now the total retarding force is
FTot = 4 194 N + 125 N = 4 319 N
To keep the car moving at constant speed, the engine must supply this force to the tires.
P = F v
v = P / F = 130 000 W / 4 319 N = 30.09 m / s
v = 30.1 m / s
On a 1-in-10 incline, the component of the weight that is parallel to the road is
F|| = w sin
= (2 500 N) (1 / 10) = 250 N
FTot = 4 194 N + 250 N = 4 444 N
P = F v = (4 444 N) (10 m / s) = 44 440 W = 44.44 kW
P = 44 440 W = 44.44 kW
| Hmwk, Ch 6 | Homework Assignment Page | PHY 1350's Home Page | Hmwk, Ch 8 |
(c) Doug Davis, 2001; all rights reserved