Homework

Ch 5, Newton's Laws of Motion

Ch5: 4, 13, 20, 24, 33, 44, 41, 50, 68

Questions 5, 7, 10, 11, 12, 14, 15, 17, 19

| Hmwk, Ch 4 | Homework Assignment Page | PHY 1350's Home Page | Hmwk, Ch 6 |

---

Additional problems from Serway's fourth edition

---

(4 ed) 5.1 Two masses, m₁ and m₂, situated on a frictionless, horizontal surface are connected by a massless string. A force, F, is exerted on one of the masses to the right (Fig P5.38). Determine the acceleration of the system and the tension, T, in the string.

---

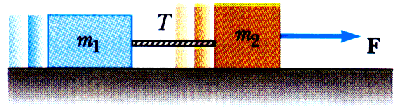
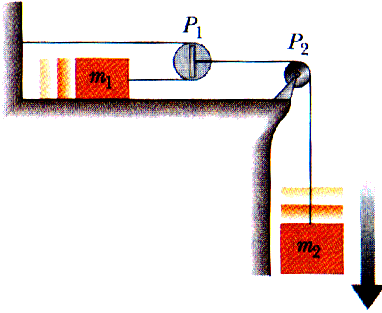
(4 ed) 5.2 Mass m₁ on a frictionless horizontal table is connected to mass m₂ through a massless pulley P₁ and a massless fixed pulley P₂ as shown in Figure P5.46.

---

(4 ed) 5.3 Find the tension in each cord for the systems shown in Figure P5.26. (Neglect the mass of the cords!).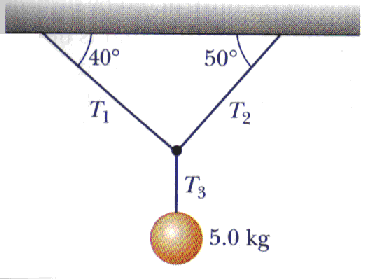

---

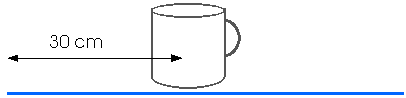
(4 ed) 5.4 A magician attemps to pull a tablecloth from under a 200-g mug located 30 cm from the edge of the cloth. If there is a frictional force of 0.10 N exerted on the mug by the cloth, and the cloth is pulled with a constant acceleration of magnitude 3.0 m/s², how far does the mug move on the tabletop before the cloth is completely out from under it? (Hint: The cloth moves more than 30 cm before it is out from under the mug!)

As always, a good diagram is essential!

---

Additional problems from Serway's fourth edition

---

Q5.5 Identify the action-reaction pairs in the following situations:
a man takes a step;

The man's foot pushes on the sidewalk and the sidewalk pushes back on his foot.

a snowball hits a woman in the back;

The snowball exerts a force on the woman's back and the woman's back exerts a force on the snowball (this force probably stops the snowball).

a baseball player catches a ball;

The baseball player exerts a force on the ball (causing the ball to stop) and the ball exerts a force on the baseball player (which he "feels" in his hand).

a gust of wind strikes a window.

The wind exerts a force on the window and the window exerts a force back on the wind, changing its direction.

---

Q5.7 If a car is traveling westward with a constant speed of 20 m/s, what is the resultant force acting on it?

If the direction is constant -- as it is here with constant speed and constant direction -- then the acceleration is zero and that means the resultant force is zero as well.

---

Q5.10 What is wrong with the statement, "Because the car is at rest, no forces are acting on it."? How ould you correct this statement?

"Because the car is at rest, the resultant force acting on it is zero."

There may be many forces acting on it -- but the vector sum of all the forces is zero since its acceleration is zero.

---

Q5.11 Suppose you are driving a car along a highway at a high speed. Why should you avoid slamming on your brakes if you want to stop in the shortest distance? Tht is, why should you keep the wkeels turning as your brake?

---

Q5.12 If you have ever taken a ride in an elevator of a high-rise building, you may have experienced a nauseating sensation of "heaviness" and "lightness" depending on the direction of the acceleration. Explain these sensations. Are we truly weightless in free-fall?

---

Q5.14 In an attempt to define Newton's third law, a student states tha the action and reaction forces are equal in magnitude and opposite in directon to each other. If this is the case, how can there ever be a net force on an object?

The forces in the action/reaction pairs act on different objects.

---

Q5.15 What forces cause

(a) a propeller-driven airplane to move?

The propellers exert a force on the air and the air experts an equal and opposite force on the propellers.

(b) a rocket?

The rocket engine exerts a force on the expanding gases (fuel and oxygen) and those gases exert a force back on the rocket engine.

(c) a person walking?

A person's foot exerts a backward force on the floor and the floor exerts a forward force on the person's foot.

---

Q5.17 If you push on a heavy box that is a rest, you must exert some force to start its motion. However, once the box is sliding, you can apply a smaller force to maintain that motion. Why?

You must exert a horizontal force equal to or greater than the force of friction. The force of static friction -- when the box is still at rest -- is greater than the force of sliding friction (or kinetic friction).

---

Q5.19 As a rocket is fired from a launching pad, its speed and acceleration increase with time as its engines continue to operate. Explain why this occurs even thought the force of the engines exerted on the rocket remains constant.

As fuel and oxygen are burned, the mass of the rocket decreases. From Newton's Second Law, F = m a, a smaller mass will have a greater acceleration if the force remains constant.

Problems from the current (5th) edition of Serway and Beichner.

While it is easier to think of the speed in units of km/h, it is easier to do the calculations if we know the speed in units of m/s. Therefore, we start with a simple units conversion -- remember, converting units is just "multiplying by 'one'".

v_f = 80 km/h [^{1 000 m}/_km][^h/_{3 600 s}]

v_f = 22.2 m/s

Now we're ready for the "real" problem. We need to apply Newton's Second Law, F = ma, to find the acceleration and then use our normal kinematics equation, v_f = v_o + a t, to find the time.

F = m a

750 000 N = (15 000 000 kg) a

a = 750 000 N / 15 000 000 kg

a = (750 000/15 000 000) m/s²

a = 0.05 m/s²

v_f = v_o + a t

22.2 m/s = 0 + (0.05 m/s²) t

t = (22.2/0.05) s

t = 444 s

t = 7.4 min

5.13 If a man weighs 900 N on Earth, what would he weigh on Jupiter, where the acceleration due to gravity is 25.9 m/s²?

w = m g

900 N = m (9.8 m/s²)

m = (900/9/8) kg

m = 91.84 kg

w_J = m g_J

w_J = (91.84 kg) (25.9 m/s²)

w_J = 2379 N

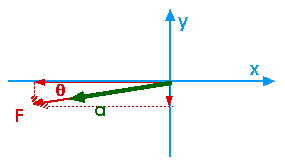
5.20 Three forces, given by F₁ = ( - 2.00 i + 2.00 j ) N, F₂ = (5.00 i - 3.00 j ) N, and F₃ = - 45.0 i N act on an object to give it an acceleration of magnitude 3.75 m/s².

(a) What is the direction of the acceleration?

From Newton's Second Law, F = m a

we know the direction of the acceleration is the same as the direction of the net force

F_net = F = F₁ + F₂ + F₃

Of course, this one vector equation really means two scalar equations

F_net,y = F _y = F_1y + F_2y + F_3y

and

F_net,x = F_x = F_1x + F_2x + F_3x

F_net,x = F_x = ( - 2.00 + 5.00 - 45.0 ) N = - 42.0 N

F_net,y = F _y = (2.00 - 3.00 + 0 ) N = - 1.00 N

tan = ^opp / _adj = | R_y | / | R_x | = 1 / 42 = 0.0238

= tan^-1 ( 0.0238 ) = 1.4^o

measured from the negative x-axis, as shown in the diagram

F = SQRT [ F_x² + F_y² ] = SQRT [ ( - 42 )² + ( - 1 )² ] = 42.01 N

(b) What is the mass of the object?

F = m a

m = F / a = (42.01 N) / (3.75 m/s²) = 11.20 kg

(c) If the object is initially at rest, what is its speed after 10.0 s?

v = v_i + a t

v = 0 + (3.75 m/s²) ( 10 s ) = 37.5 m/s

(d) What are the velocity components of the object after 10.0 s?

v = v_i + a t

v _x = - v cos = - (37.5 m/s) (0.9997) = 37.5 m/s

v _y = - v sin = - (37.5 m/s) (0.0238) = 0.893 m/s

5.24 A bag of cement weighs 325 N and hangs from three cables as shown in Figure P5.24. Two of the cables make angles of ₁ = 60^o and ₂ = 25^o with the horizontal. If the system is in equilibrium, find the tensions T₁, T₂, and T₃.

Clearly

T₃ = w = 325 N

In terms of components,

T_3x = 0

T_3y = - 325 N

Look at all the forces at the knot or the junction where the three cables come together,

T₁ + T₂ + T₃ = 0

But remember this is a vector equation so it really means

5.33 A block is given an initial velocity of 5 m/s up a frictionless 20^o incline. How far up the incline does the block slide before coming to rest?

First, make a good, clear free-body diagram of all the forces on the block. Then determine the net force and use that to find the acceleration.

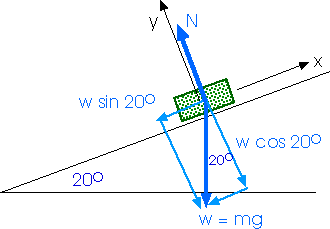
Since the block is going to move along the incline, choose that direction for the x-axis and the perpendicular as the y-direction and then resolve the forces into their components. Remember, while it is convenient to write F = m a, that always means F_net = m a. We always need the net force.

(a) What angle does the strap make with the horizontal?

(b) What normal force does the floor exert on the suitcase?

Draw in all the forces acting on the suitcase.

 

(a) What is the angle ?

F_x = (35 N) cos

F_y = (35 N) sin

w = (20 kg) (9.8 m/s²) = 196 N

F_y = F_y + n - w = 0

(35 N) sin + n - 196 N = 0

F_x = F_x - 20 N = 0

F_x = 20 N

(35 N) cos = 20 N

cos = 20 / 35 = 0.571

= 55^o

(b) What normal force does the ground exert on the suitcase?

F_y = F_y + n - w = 0

(35 N) sin + n - 196 N = 0

(35 N) sin 55^o + n - 196 N = 0

(35 N) (0.821) + n - 196 N = 0

28.7 N + n - 196 N = 0

n = 167.3 N

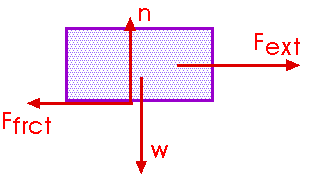
For this special or particular case of a horizontal surface, the normal force n turns out to be equal to the weight w because of F_y = w - n = m a_y = 0

since there is no acceleration in the vertical direction.

n = w = mg

F_x = F_ext - F_frict = m a_x

Initially the block is at rest, so a_x = 0

F_frict = F_ext = 75 N

F_frict = _s n = _s m g = _s (25 kg) (9.8 ms/²) = _s 245 N

_s 245 N = 75 N

_s = 0.31

Once the block starts to move, a smaller external force,

F_ext = 60 N

keeps it moving with a_x = 0.

F_frict = F_ext = 60 N

F_frict = _k n = _k m g = _k (25 kg) (9.8 ms/²) = _k 245 N

_k 245 N = 60 N

_k = 0.24

(Different printings of Serway's text have different values of the masses!)

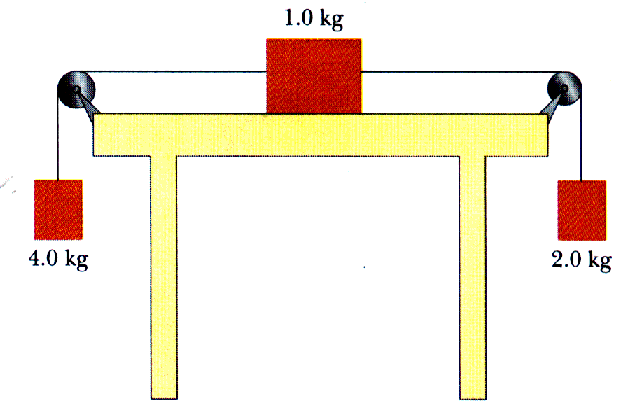
(a) Determine the acceleration of each block and their directions.

(b) Determine the tensions in the two cords.

The 4.0 kg block should accelerate downward. The 2.0 kg block should accelerate to the left. The 1.0 kg block should accelerate upward. Draw three clear free-body diagrams for the three masses.

Do not draw in all the forces on a single diagram. That gets far too confusing!

For the 4.0 kg mass and its motion, take the downward direction to be positive.

F_net = w - T_l = m a

m g - T_l = m a

(4.0 kg) (9.8 m/s²) - T_l = (4.0 kg) a

39.2 N - T_l = (4.0 kg) a

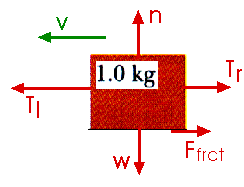
Since the 1.0 kg block slides to the left, the force of friction, F_frct, is directed toward the right.

F_net,y = n - w = m a_y = 0

n = w = (1.0 kg) (9.8 m/s²) = 9.8 N

Therefore,

F_frct = n = (0.35) (9.8 N) = 3.43 N

F_net,x = T_r + F_frct - T_l = m ( - a)

Notice that we have put the acceleration in with a minus sign, as - a, since we expect the acceration to be to the left and we have taken right to be positive. Notice, too, that the tension need not be the same on the left as on the right.

T_r + 3.43 N - T_l = (1.0 kg) ( - a)

Since this 2.0-kg mass accelerates upward, we will take up as positive.

F_net = T_r - w = m a

T_r - m g = m a

T_r = m g + m a

T_r = (2.0 kg) (9.8 m/s²) + (2.0 kg) a

T_r = 19.6 N + (2.0 kg) a

Now we have a set of three simultaneous equations in three unknowns, a, T_r, and T_l.

39.2 N - T_l = (4.0 kg) a

T_r + 3.43 N - T_l = (1.0 kg) ( - a)

T_r = 19.6 N + (2.0 kg) a

Solve for T_l from the first one,

T_l = 39.2 N - (4.0 kg) a

We already have T_r from the third one. Now substitute those values into the second equation,

T_r + 3.43 N - T_l = (1.0 kg) ( - a)

[19.6 N + (2.0 kg) a] + 3.43 N - [39.2 N - (4.0 kg) a] = (1.0 kg) ( - a)

[19.6 + 2.0 a] + 3.43 - [39.2 - 4.0 a] = - a

[19.6 + 2.0 a] + 3.43 - [39.2 - 4.0 a] = - a

(2 + 4 + 1) a = 39.2 - 3.43 - 19.6

7 a = 16.17

a = 2.31

a = 2.31 m/s²

Now we can use this to find the tensions.

T_l = 39.2 N - (4.0 kg) (2.31 m/s²)

T_l = 39.2 N - 9.2 N

T_l = 30.0 N

T_r = 19.6 N + (2.0 kg) a

T_r = 19.6 N + (2.0 kg) (2.31 m/s²)

T_r = 19.6 N + 4.6 N

T_r = 24.2 N

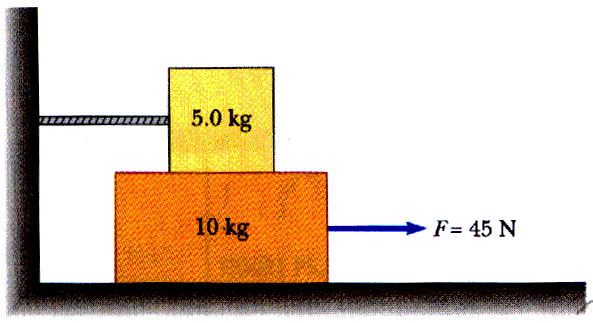
(a) Draw a free-body diagram for each block and identify the action-reaction forces between the blocks.

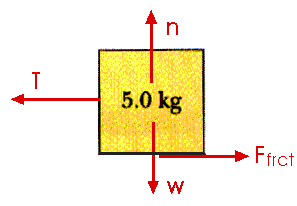
F_net,x = F_frct - T = m a_x = 0

F_frct = T

a_x = 0 since this block does not move.

F_net,y = n - w = m a_y = 0

n = w = m g = (5.0 kg) (9.8 m/s²) = 49 N

F_frct = n = (0.20) (49 N) = 9.8 N

F_frct = 9.8 N

(b) Determine the tension in the string and the magnitude of the acceleration of the 10-kg block.

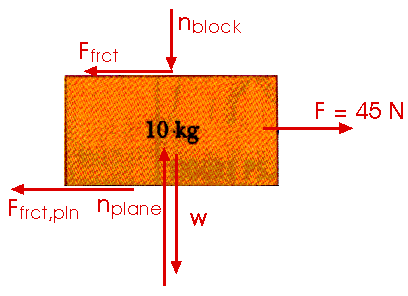
The two friction forces F_frct are an action - reaction pair of forces; these are the forces of friction exerted by each block on the other. We already know the value of these forces, F_frct = 9.8 N

The two normal forces exerted on the blocks by each other are an action-reaction pair. We already know the value of these forces,

n_block = 49 N

Now we can apply Newton's Second Law to this 10-kg mass,

F_net,y = n_plane - w - n_block = 0

n_plane - (10 kg) (9.8 m/s2) - 49 N = 0

n_plane = 147 N

This allows us to calculate the friction force exerted by the plane on the bottom block, F_frct,plane.

F_frct,plane = n_plane = (0.2) (147 N) = 29.4 N

Now we know all the forces acting on the 10-kg mass,

F_net,x = 45 N - F_frct - F_frct,plane = m a

45 N - 9.8 N - 29.4 N = (10 kg) a

5.8 N = (10 kg) a

a = 0.58 m/s²

Additional problems from the fourth edition of Serway

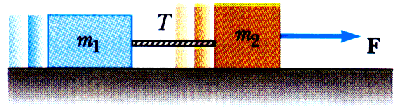
Draw a free-body diagram for each mass.

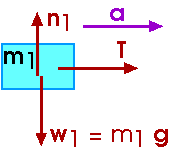
Very little of interest happens in the y-direction for this problem. From the y-components of the forces on the two masses we find that

n₁ = m₁ g

n₂ = m₂ g

This information would be useful -- and necessary -- if there were friction present. Since this is a frictionless surface, this information is merely interesting.

But, from the x-components of the forces, we have

F_1x = T = m₁ a

F_12x = F - T = m₂ a

These form a system of two simultaneous equations with two unknowns,

F - (m₁ a) = m₂ a

F = m₁ a + m₂ a

F = ( m₁ + m₂ ) a

a = F / (m₁ + m₂)

T = m₁ a

T = m₁ F / (m₁ + m₂)

T = [ m₁ / (m₁ + m₂) ] F

(a) If a₁ and a₂ are the magnitudes of the accelerations of m₁ and m₂, respectively, what is the relationship between these accelerations?

Why is there a question about a₁ and a₂ rather than just "the acceleration?

Look at pulley P₁. What happens when it moves a distance x (or what happens when it moves a distance of 1 cm)? Mass m₂ also moves a distance x (or 1 cm) but mass m₁ moves twice that distance, 2 x (or 2 cm)! That means that the distance m1 moves is twice the distance moved by m₂, or

x₁ = 2 x₂

So the velocity of m₁ must be twice the velocity of m₂

v₁ = 2 v₂

and the acceleration of m₁ must be twice the acceleration of m₂,

a₁ = 2 a₂

Find expressions for (b) the tensions in the string and

(c) the accelerations a₁ and a₂ in terms of m₁, m₂, and g.

Draw good free-body diagrams for the forces on each mass and on pulley P1

From the forces on mass m₁, we find

T₁ = m₁ a₁

and

n = w₁ = m₁ g

From the forces on pulley P₁, we can see that

2 T₁ = T₂

Since mass m₂ is accelerating downward, let's take down as positive this time.

F = w₂ - T₂ = m₂ a₂

m₂ g - T₂ = m₂ a₂

T₂ = m₂ g - m₂ a₂

T₂ = m₂ ( g - a₂ )

2 T₁ = m₂ ( g - a₂ )

2 m₁ a₁ = m₂ ( g - a₂ )

2 m₁ (2 a₂) = m₂ ( g - a₂ )

4 m₁ a₂ = m₂ g - m₁ a₂

5 m₁ a₂ = m₂ g

a₂ = m₂ g / 5 m₁

a₂ = ( m₂ / 5 m₁ ) g

a₁ = 2 a₂

a₁ = 2 m₂ g / 5 m₁

a₁ = ( 2 m₂ / 5 m₁ ) g

T₁ = m₁ a₁

T₁ = ( 2 m₂ / 5 m₁ ) m₁ g

T₁ = ( 2 m₂ / 5 ) g

T₁ = ( 2 / 5 ) m₂ g

T₂ = 2 T₁

T₂ = ( 4 / 5 ) m₂ g

T₃ = w = m g = (5.0 kg ) (9.8 m/s²) = 49 N

F_net = F = T₁ + T₂ + T₃ = 0

F_net,x = F_x = T_1x + T_2x + T_3x = 0

T_1x + T_2x + T_3x = - T₁ cos 40^o + T₂ cos 50^o + 0 = 0

- T₁ (0.766) + T₂ (0.643) = 0

0.766 T₁ = 0.643 T₂

T₁ = 0.643 T₂ / 0.766

T₁ = 0.839 T₂

F_net,y = F_y = T_1y + T_2y + T_3y = 0

T_1y + T_2y + T_3y = T₁ sin 40^o + T₂ sin 50^o - 49 N = 0

T₁ sin 40^o + T₂ sin 50^o = 49 N

T₁ (0.643) + T₂ (0.766) = 49 N

(0.839 T₂ ) (0.643) + T₂ (0.766) = 49 N

(0.539 + 0.766) T₂ = 49 N

1.305 T₂ = 49 N

T₂ = 49 N / 1.305

T₂ = 37.53 N

T₁ = 0.839 T₂ = 0.839 (37.53 N)

T₁ = 31.49 N

T₃ = w = m g = (10.0 kg ) (9.8 m/s²) = 98 N

F_net = F = T₁ + T₂ + T₃ = 0

F_net,x = F_x = T_1x + T_2x + T_3x = 0

T_1x + T_2x + T_3x = - T₁ cos 60^o + T₂+ 0 = 0

- T₁ (0.500) + T₂ = 0

0.500 T₁ = T₂

F_net,y = F_y = T_1y + T_2y + T_3y = 0

T_1y + T_2y + T_3y = T₁ sin 60^o + 0 - 98 N = 0

T₁ (0.866) = 98 N

T₁ = (98 / 0.866) N

T₁ = 113.2 N

T₂ = 0.500 T₁ = 0.500 (113.2 N)

T₂ = 56.6 N

T₃ = 98 N

As always, a good diagram is essential!

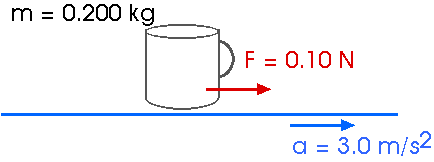
The acceleration of the mug is

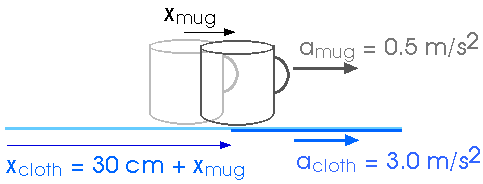
During time t, the mug moves a distance

During this same time t, the table cloth moves a distance

Taking into account the extra 30 cm -- or 0.30 m -- that the table cloth must move, we can set

and solve for the time and then go back and calculate x_mug.

| Hmwk, Ch 4 | Homework Assignment Page | PHY 1350's Home Page | Hmwk, Ch 6 |

(c) Doug Davis, 2001; all rights reserved