Figure 20.13 illustrates the interference pattern of a single slit. If light passes through a large opening in a card the shadow is sharp and just the size we would expect. However, if light passes through a narrow slit, some unusual things happen. First, as the slit is made narrow, the light that passes through spreads out to a wider angle. As the slit is made more narrow, the light spreads out even more through a greater angle. We can explain this by Huygen's Principle. As the slit becomes very narrow, the light comes from the slit as if it were a new source, like the long, narrow filament of a light bulb.

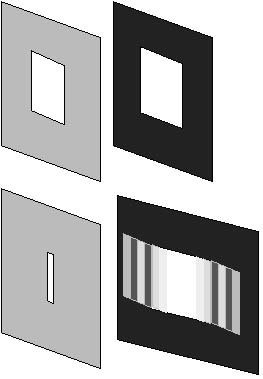
In addition to this spreading of the light, there are dark and bright bands present. These are the result of interference or diffraction between light coming from different parts of the single slit.

Light spreads out as it passes through a slit when the width of the slit is approximately the size of a wavelength of light. This means that light with longer wavelengths (like red) will spread out more than light with shorter wavelengths (like blue or violet).

While this is true for light it is also true for all other waves. No matter how carefully the lenses in a microscope are made, there will be diffraction effects or limitations because of the wave nature of light itself. Microscopes can see better-that is, sharper images will be formed and more detail can be seen-if ultra-violet (UV) light is used. Later, when we study Modern Physics, we will find that electrons behave as waves with very small wavelengths. Electron microscopes can provide more information and larger magnification than optical microscopes because the electrons' wavelength is so much smaller.

On a larger scale the same diffraction effects come into play with radio waves. AM radio waves, with frequencies of 540 kHz to 1700 kHz, have wavelengths between 180 meters and 6,000 meters! Almost anything they encounter will be small compared to their wavelength. This means these radio waves readily spread around buildings and towers and hills.

FM radio waves, with frequencies of 88 MHz to 108 MHz, have wavelengths between 2.7 meters and 3.7 meters. Therefore, hills or towers or buildings may cast a "shadow" to such waves. FM reception is often more difficult than AM reception for just that reason.

Figure 20.14 illustrates the shadows of some common objects. These shadows were made by illuminating objects with a tiny point source of light or a laser. These are not the common, sharp shadows to which we are accustomed; instead, the edges show a set of fringes not unlike the interference fringes of Young's double slit experiment. These entire sets of fringes are referred to as diffraction patterns and are caused by the same wave interference as in the double slit experiment.

The first photo in figure 20.14 deserves special interest. Following Young's Double Slit experiment, Augustin Fresnel presented a rather complete wave theory of light to the French Academy in 1819. Simeon Poisson pointed out that if Fresnel's wave theory was correct, the shadow of a disk cast by a point source of light should have a bright spot at its center. The coherent light from a point source (or a laser) diffracts around the edge of the disk and the light that arrives at the center interferes constructively to produce a bright spot. This very unexpected result was experimentally verified by Francois Arago and this is now known as "Arago's spot". Of course, the experimental verification of such an unexpected result provided an additional strong argument for the wave theory of light.

Any object, when illuminated by such coherent light from a point source or a laser produces diffraction patterns like those in the figure. We do not commonly see these diffraction patterns because most light sources are extended sources and the diffraction pattern created by light from one point on the light source is obscured by other patterns from other points on the light source. Most light sources are also incoherent so the pattern produced at one instant is obscured by the pattern produced a moment later. If more than one wavelength, or color, is present the maxima and minima will occur in different places for each wavelength and the diffraction pattern will be made of colored fringes.

You can think of ordinary screen wire as a collection of tiny slits. Light spreads out when it passes through a slit. Ordinary screen wire produces a diffraction pattern that takes small sources of light and spreads the light into a very wide pattern. Since screen wire is composed of "slits" that run both horizontally and vertically, the diffraction pattern is spread out vertically and horizontally and looks like a cross or a star. Photographic filters work the same way. A filter made of fine horizontal and vertical lines produces a cross just like screen wire while a filter made of three sets of fine lines, each rotated 60, produces a six-pointed "star". Examples are shown in Figure 20.15.

The star in a star sapphire is a similar diffraction pattern produced by the three-dimensional pattern in the crystal structure of the sapphire as shown in Figure 20.16.