The diffraction grating of Figure 20.9 looks much like a series of double slits; and, indeed, it is just that. Just as for the arrangement in Young's double slit experiment, light traveling from one slit travels a distance greater than the light from an adjacent slit. Just as with the double slit, this additional distance determines how one wave combines with or interferes with the waves from adjacent slits.

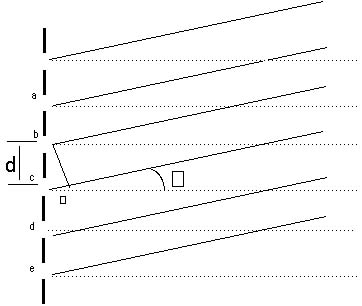
Again, just as with the double slit, if this distance is exactly one wavelength-or two, or three or any integral number of wavelengths-waves from two adjacent slits will arrive in phase and constructive interference will occur. From Figure 20.10 you can also see that light from each slit travels an integral number of 's compared to the light from any other slit. If is a wavelength (or an integer times a wavelength, = m ) so that light from two adjacent slits interfere constructively, then light from all the slits interferes constructively and a bright area or maximum will be seen. Just as for the double slit, we find bright regions for

= m (bright)

where m is an integer (m = 0, 1, 2, ...).

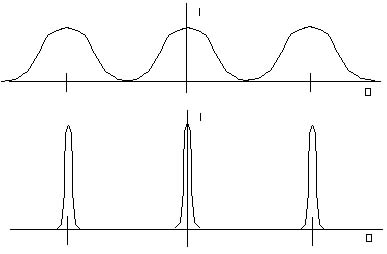
So far, this seems just to have repeated the results of the double slit experiment. The difference-the very useful difference-comes when we look at the details of the intensity pattern as sketched in Figure 20.11 which shows a graph of the intensity pattern for a double slit and for a diffraction grating. For a double slit, the intensity gradually falls from a maximum to a minimum of zero and then gradually increases again. But for a diffraction grating, the intensity drops off far more quickly. In effect, these maxima become sharp, distinct lines. 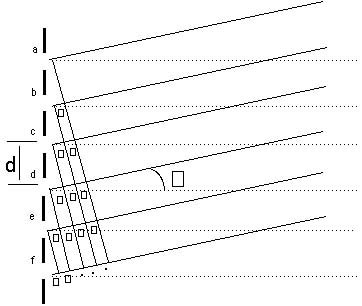To understand this, look back at Figure 20.10. Light from each slit travels a distance farther than light from its adjacent slit. Let = (1/10) for a moment. Then light from one slit, such as slit a, will be completely out of phase with light from another slit five slits away, slit f in this case, and these will destructively interfere. Light from each slit will undergo destructive interference with light from another slit, five slits away. With many slits, any angle other than those which provide constructive interference will have zero intensity due to this destructive interference. The bright lines from a diffraction grating will be very sharp.

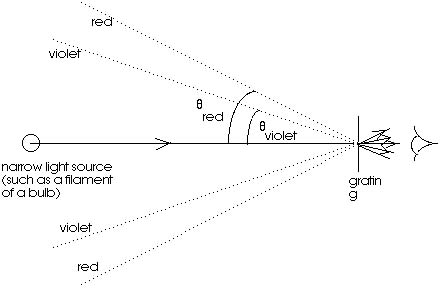
Bright lines of constructive interference occur for = m. As the wavelength varies, so will the angle for which constructive interference occurs. If we have white light with a full range of wavelengths from = 400 nm for violet light to =700 nm for red light, each wavelength-or each color-will have constructive interference at a different angle. This means that when we look at a white light source-like the filament of a bulb-we will see each color at a different position. This produces a spectrum of colors much like what we saw when white light passed through a prism. This is illustrated in Figure 20.12.