|
|

|
|

But how are the notes placed between octaves? Pythagoras, in the
fifth century BC, noted that harps made pleasant sounds if the
lengths of their strings were proportional to small integers.
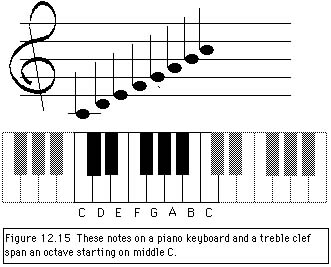
Figure 12.15 shows the notes on a piano keyboard and a treble
clef that span an octave starting on middle C. The notes C, E,
and G have frequencies in the ratio of 4:5:6. When they are played
together, the three notes blend very well and are pleasant to
the ear; these notes form a major triad or a major chord.
The frequency of middle C is 262 Hz. That and requiring the pleasing
tones of a major triad, then determine the frequencies (or pitches)
of E (262 Hz x (5/4) = 327.5ÊHz) and G (262 Hz x (6/4) =
393 Hz). C', being an octave higher than middle C, has a frequency
of 524 Hz. The notes F, A, C' also form a major triad (or a major
chord) and that determines the frequency (or pitch) of notes F
(524 Hz x (4/6) = 349 Hz) and A (524 Hz x (5/6) = 437 Hz). Likewise,
the notes G, B, and D' also form a major triad (or a major chord
and that determines the frequency (or pitch) of notes B (393 Hz
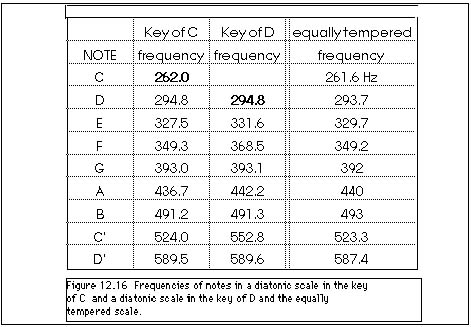
x (5/4) = 491 Hz) and D' (393 Hz x (6/4) = 589.5 Hz). Figure 12.16
lists the frequencies of all the white notes on a piano if we
tune to these major triads having started with middle C. This
is called a diatonic scale in the key of C. However, we could
have started with a different note. Figure 12.16 also lists the
frequencies of all the white notes on a piano if we tune to these
major triads starting with D above middle C. This is called a
diatonic scale in the key of D. You can see that some of the frequencies
are the same but most are somewhat different!
This means we could tune a piano to a diatonic scale in the key of C but then it would sound funny if we tried to play something written in the key of D. Major triads or chords that should sound pleasant together would no longer sound good. During the eighteenth century pianos and harpsichords-and all instruments-were tuned to a particular key for a particular musical piece. They would have to be retuned to a different key for the performance of a different piece written in a different key.
To avoid all the labor and tedium in this retuning, the scheme of an equally tempered scale has been devised. Including the black keys-the sharps and flats-on a piano keyboard, there are twelve notes, called half-steps, between C and C'. We require that the frequency of C' be twice that of C and that the ratio of the frequencies of neighboring half-step notes or keys be the same. That means the ratio of frequencies of neighboring keys must be the twelfth root of 2, (that is, (1.05946)12 = 2). That is, if the frequency of each key is 1.06 times the frequency of the neighboring key, by the time you move from middle C, through twelve keys, and arrive at C' an octave higher, the frequency of C' will be exactly 2 times the frequency of middle C. Figure 12.16 also lists the frequencies of the notes of this equally tempered scale. This is a compromise so that notes and chords of all keys sound equally good (or bad) when played on this scale.

|
|