Figure 12.17 illustrates beats for two waves with frequencies of 10 Hz and 12 Hz (of course, those frequencies are well below the range of human hearing. But it is easier to illustrate this idea with frequencies that are small numbers). In one second, the 10 Hz wave has sent out ten waves and the 12 Hz wave, twelve. What we receive is the superposition of those two waves. When the two waves are "in phase" the resulting superposition has a large amplitude. When the two waves are "out of phase" the resulting superposition has a small amplitude. From Figure 12.17 you can see that the superposition has an envelope-or general appearance-that shows a frequency of 2 Hz.

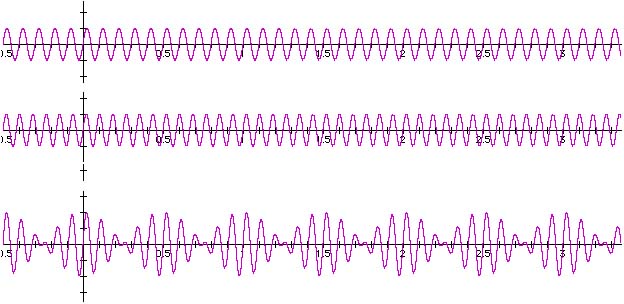
The beat frequency is the frequency with which the volume oscillates, wavers, or increases and decreases; it is the frequency of the "envelope" or general appearance of the wave. This beat frequency is the difference in the frequencies of the two waves. For the example shown here in Figure 12.17, the beat frequency is 2 Hz = 12 Hz - 10 Hz.

If two violins play the note A and one is correctly tuned to 440 Hz but the other is slightly low at 437 Hz, beats of 3 Hz will be heard. That is, the resulting sound of these two violins playing an A will waver or oscillate three times a second. This resulting annoying sound means the two violins are out of tune. As the lower violinist tightens the A-string and brings it up to, say, 439 Hz, the beat frequency will change to only one Hz. As the A-string is tightened more and that violin, too, approaches the correct 440 Hz, the beat frequency will become slower and slower and finally disappear as the two violins are correctly tuned. Thus, beat frequencies-or their elimination-are often used to tune musical instruments.