

Electric Potential
Electric Potential due to
Continuous Charge Distributions When we looked at electric fields, we developed Coulomb's Law for the field from a point charge and then used that to find the electric field due to a continuous distribution of charge. Now, as we look at electric potential, we do the same thing. However, this time it will be easier since electric potential is a scalar. No directions or components are required.
Consider a point P in space. What is the electric potential there because of a continuous distribution of charge? For some little amount of charge dq, there is a contribution to the electric potential at P; that contribution dV is
dV = k (dq / r)
where r is the distance from point P to our little amount of charge dq. Typically dq will be a charge density multipled by a differential length, area, or volume. That is, we will usually have
dq =
ds
dq =
dA
or
dq =
dV
Be careful, this dV is a small, differential volume like dV = dx dy dz. We are also using V for electric potential so dV usually means the contribution to the electric potential due to some small differential charge dq. Be careful!
We can write
But, of course, the "fun" or the work or the understanding comes from the details that depend upon the geometry of a particular situation. Therefore, let us look at some particular examples:
Consider a ring of charge. The ring has radius a and we want to calculate the electric potential at a point P on the axis of the ring, a distance x away from the ring.
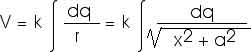
Now that we can handle a ring of charge, let us extend that geometry and integrate the ring of charge from r = 0 to r = a and use a disk of charge.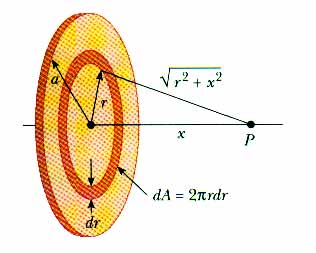
For a ring of radius r and thickness dr, the charge dq on that ring is the charge density sigma
multiplied by the area
dq = [ dA ]
dq =
[ 2
r dr ]
Make a variable substitution, u = x2 + r2 so du = 2 r dr,

Don't forget the limits!
Consider a line of charge:
Now the small differential charge dq is the charge density
multiplied by a differential length dx
dq = dx
If we have a line of charge with a length L, we will need to integrate dx from x = 0 to x = L.
Consider a line of charge as sketched here. What is the electric potential at a point P a distance d away from the end of the line of charge of length L, carrying total charge Q uniformly distributed along its length?
For a small differential charge dq located at position x, the distance to point P is r where
For such a point charge dq located a distance r away from P, we know it contributes dV to the potential at P,
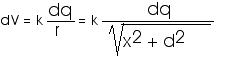
We can look this up in a table of integrals and find
But don't forget the limits!
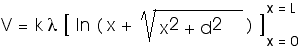
We have calculated the electric potential. We could use these expressions andE = - dV/dx or
E = - dV/dr to calculate the electric field from these distributions.
Return to Ch25 ToC (c) Doug Davis, 2002; all rights reserved