Electric Fields

The Electric Field

Due to Continuous Charge Distributions

 

Coulomb's Law tells us the force between two point charges. Our variation tells us the Electric field due to a single point charge. What do we do if we have a continuous charge distribution? We can sum up the electric field caused by each tiny, infinitesimal part of the charge distribution. This means an integral over the charge distribution:

For a single point charge Q, we had

where r is the distance from the charge Q. Remember, E is only the magnitude of the electric field; we must take care of its vector nature separately! That's important! Now we have a distribution of charge and we must replace Q by dQ and E by dE -- and take care of the direction of E.

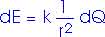
r, the distance from the tiny, elemental, infinitesimal charge dQ to the point in question, is a function of where that charge dQ is. And, what does it mean to "integrate over the charge dQ"? We know how to integrate over a variable like dx, or a plane like dA = dx dy or dA = 2 r dr or dA = r d dr, or a volume like dV = dx dy dz. So we will need to change from this symbolic charge dQ to a charge density multiplied by some spatial differential,

dQ = dx

dQ = dA

dQ = dV

Look at Example 23.7 in Serway's and Beichner's textbook (p.724): A rod of length has a uniform charge per unit length and a total charge Q. Calculate the electric field at a point P along the axis of the rod, a distance d from one end.

 

What is the electric field at point P because of a little piece of charge Q located at position x, as shown in the sketch?

E = k Q / x²

We will carry out an integration from x = d to x = d + so we need to change this small amount of charge Q into a small length x,

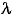
  Q = x

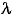
E = k ( x) / x²

where

= Q /

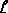
dE = k ( dx) / x²

dE = k (dx / x²)

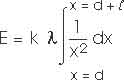
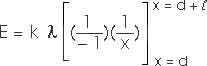
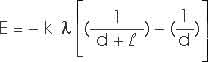
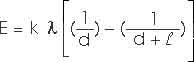
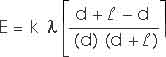
What about other geometries?

---

Look at Example 23.8, on page 724, of Serway's and Beichner's text. Find the electric field due to a ring of charge: A ring of radius a has a uniform charge density with a total charge Q. Calculate the electric field along the axis of the ring at a point P, a distance x from the center of the ring.

The charge density is

= Q / (2 a)

Remember, our equation for the electric field is for the magnitude of the electric field. Consider a little piece of charge dq as sketched in the diagram. Because that charge dq is there, there is an electric field dE at point P in the direction shown. The component dEx of that electric field along the direction of the axis perpendicular to the plane of the ring is

dE_x = dE cos

dE_x = dE (x/r)

dE_x = [k dq/r²] (x/r)

dE_x = [k dq/r³] x

dE_x = [k x dq/r³]

dE_x = [k x/r³] dq

Notice that, with this geometry, once the radius of the ring a is specified and the position x, that fully specifies r. r and x do not change as we integrate over dq.
[[ Remember, SQRT() means "square root of ()" because that is easier for me to type. ]]

r = SQRT(a² + x²)

r³ = (a² + x²)^3/2

1/r³ = 1/(a² + x²)^3/2

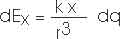
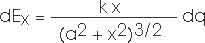
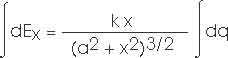
Remember, x and a are not variables.

What about the component of E that is perpendicular to this direction? By symmetry that component is zero. From the diagram, you can see that for each element of charge dq, there is another element of charge dq on the opposite side of the ring that causes an electric field that just cancels the first one -- that is, their components perpendicular to the axis of symmetry just cancel. Notice that their components along the axis do not cancel for they lie in the same direction. Diagrams are very important. Don't start writing equations before you have made good, clear, complete diagrams!

---

Now that we have looked at the electric field because of a ring of charge, we can build upon that and extend our ideas and look at the electric field due to a disk of charge. Look at Example 23.9, on page 725 of Serway's and Beichner's textbook.

A disk of radius R has a uniform charge per unit area . Calculate the electric field at a point P that lies along the central axis of the disk and a distance x from its center.

Consider a ring of charge as sketched here. The ring has a radius of r and a thickness of dr and carries a charge of dq. But that charge dq is just proportional to the area,

dq = dA

dq = [C dr]

dq = [ (2 r) dr ]

dq = 2 r dr

Think back on what we just did in the previous example. For charge Q on a ring of radius r, we found that the electric field at a distance x from the plane of the ring was

That is exactly what we have now -- except we have charge dq instead of Q and the ring has a radius of r instead of a. So we can write

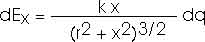
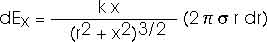
Be careful; the limits of integration are important.

We could look this up in a table of integrals. But a variable substitution is still fairly direct and straightforward;

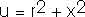
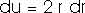
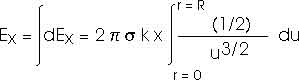
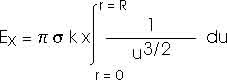
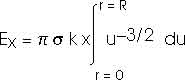
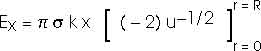
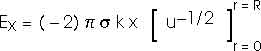
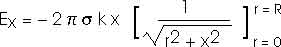
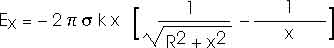
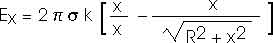
This result is only valid for x > 0 and must be modified slightly for x < 0.

Electric Field			E-Field Lines
Return to Ch23 ToC

(c) Doug Davis, 2002; all rights reserved