Mass in Special Relativity

m =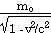

Again, the speed of light is a universal speed limit!

In Special Relativity, the kinetic energy turns out to be given by

KE = - m_oc²

or

KE = m c² - m _oc²

Whatever happened to

KE = (¹/₂) m v²

Surprisingly, these two expressions turn out to be the same for v << c (as they must).

KE = m c² - m _oc²

E_rest = m_oc²

E_total = m c² =

KE = E_total - E_rest

Mass and energy are really the same thing!

E = m c²

The very unexpected part is that an object of mass m has rest energy--that it has energy just because it has mass. We must talk about the Conservation of Mass-Energy rather than Conservation of Energy alone or Conservation of Mass alone. Energy will increase if mass decreases; mass can be turned into energy. If the mass increases, energy must be supplied; energy can be turned into mass. Mass and energy are interchangeable. Mass and energy are the same thing.

---

Example: A deuteron is the nucleus of an atom of "heavy hydrogen" and is composed of one proton and one neutron. Use the masses of a proton, a neutron, and a deuteron and explain the energy consequences of these masses.

Reasoning and Solution: From a table we can find the masses:

m_p = 1.007276 u

m_n = 1.008665 u

m_d = 2.013553 u

where m_p, m_n, and m_d are the masses of a proton, neutron, and deuteron, respectively, measured in "unified mass units u" where

u = 1.66 x 10^-27 kg

The total mass of the proton and neutron separately is

m_tot = m_p + m_n = 2.015941 u

so the mass difference is

m = (m_p + m_n) - m_d = 0.002388 u

That is, the proton and neutron, when separate, have 0.002388 u mass more than when they are bound together as a deuteron. According to our mass-energy equation, E = m c², that means the deuteron has

E = m c² = (0.002388 u)(1.66 x 10^-27 kg/u)(3.0 x 10⁸ m/s)²

E = 3.56 x 10^-13J

E = 3.56 x 10^-13J

E = 2.23 MeV

less rest energy than its separate parts.

When a proton and neutron bind together to form a deuteron, 2.23 MeV of energy is released. Or 2.23 MeV of energy must be supplied to break apart a deuteron into a free proton and a free neutron.

---

This is precisely what happens in nuclear reactions that provide commercial nuclear power. In nuclear fusion, lighter particles fuse together to produce a heavier particle whose mass is less than the sum of the masses of the lighter particles that produced it. This loss of mass shows up as energy; this energy may be in the form of kinetic energy of the particle or photons (gamma rays) or both. In nuclear fission one massive object splits or fissions into two or more lighter ones but the sum of the resulting smaller objects is less than the original mass. Again, this loss of mass shows up as energy; this energy may be in the form of kinetic energy of the particles or photons (gamma rays) or both.

Velocity			Summary
Return to Ch 27, Special Relativity

(c) Doug Davis, 2002; all rights reserved