Velocity Transformations

As a young child, I was fascinated by the following question that my father posed to me: If a machine gun, which fires bullets at 100 miles per hour, is mounted on an airplane that flies 200 miles per hour, will the airplane run into its own bullets?

If an alien spacecraft fires photon torpedoes forward with a speed of 0.75c (with respect to the spacecraft, of course), while the spacecraft itself has a speed of 0.3c with respect to Earth, how fast are the torpedoes observed to travel with respect to Earth?

The obvious, common-sense, intuitive answer is 1.05c; this is what the Galilean Transformations would give. But velocities greater than c do all sorts of terrible things to the Lorentz Transformations. So let us investigate this situation more closely.

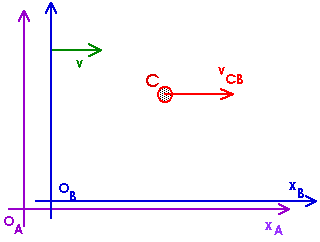
The diagram below shows our usual case of frames A and B with relative velocity v. In frame B, object C is observed to have a speed of v_CB in the x-direction. What is the speed of C with respect to A, v_CA?

This was for the x-component of the velocity, so we can write that explicitly,

Distances in the y- and z-directions are not affected, but time is affected. So the velocity components in the y- and z-directions are affected. For them, we get.

---

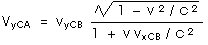
Now we have the information to answer the alien spacecraft-phaser torpedo question posed at the beginning of this section.

Example: If an alien spacecraft fires photon torpedoes forward with a speed of 0.75c (with respect to the spacecraft, of course), while the spacecraft itself has a speed of 0.3c with respect to Earth, how fast are the torpedoes observed to travel with respect to Earth?

This is illustrated below.

Reasoning: In terms of the labels we have used and the equations we have developed, the Earth-bound observer is observer A, observer B is on the spaceship, and the photon torpedo is object C. The speed of the space ship (B) with respect to Earth (A) is

v_BA = 0.30 c

or, simply

v = 0.30 c

The speed of the photon torpedo (C) with respect to the spaceship (B) is

v_CB = 0.75

We want to calculate the speed of the photon torpedo (C) with respect to Earth (A), v_CA.

Solution: This requires an application of our velocity transformation equation,

v_CA =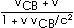

v_CA =

v_CA =

v_CA = 0.86 c

The photon torpedo will be observed by Earthbound observer A to have a speed of 0.86c. That is faster than the 0.75c in B's frame, of course, but far different than the 1.05c predicted by the Galilean Transformation. These velocity transformations reflect the fact that no inertial observer will see a real, material object traveling faster than the speed of light. The speed of light is a universal, cosmic speed limit.

Applications of the Lorentz Transformations			Mass
Return to Ch 27, Special Relativity

(c) Doug Davis, 2002; all rights reserved