

Connected Objects
Example: Two blocks of masses m1 and m2 are placed in contact with each other on a smooth, horizontal plane as shown here. A constant horizontal force F is applied to m1. What is the acceleration of each mass?

In one sense, we can (almost) solve this example intuitively -- in our head. A force F is applied to an object whose mass is m = m1 + m2. So its acceleration must be
a = F / m or
a = F / (m1 + m2) That's the right answer! But is there nothing more to this question? Simple questions -- the intuitively obvious kind -- make wonderful templates or examples for more difficult problems.
Look at all the forces on m1. Make a good free-body diagram of the forces acting on m1.
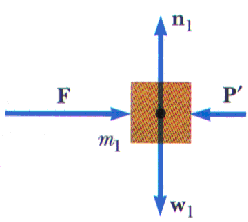
Of course the external force F pushes to the right on the mass m1. Gravity pulls down with force w1 = m1 g and the plane responds with a normal force n1. But the other mass -- m2 -- exerts a force on mass m1. This force is labeled P' and points to the left. We can apply Newton's Second Law to the y-component forces and find that n1 = w11. But now there is an additional and unknown force in the x-component of Newton's Second Law,
F1,net = F - P' = m1 a We need more information so we turn to the other mass, m2
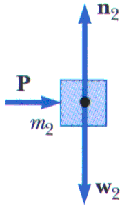
The first mass m1 exerts a force P on this mass, m2. Applying the y-component of F = m a, we readily find
n2 = w2 For the x-components, the only force acting on m2 is P so
F2,net = P = m2 a However, from Newton's Third Law, F12 = - F21, we know that P = P' so
F - P' = m1 a F - m2 a = m1 a
F = m1 a + m2 a
F = ( m1 + m2) a
a = F / ( m1 + m2)
That is the same answer we found so quickly earlier but this may provide a pattern to use for more complex situations.
Example: This particular example is stated in terms of weighing a fish in an accelerating elevator. It is also fun to think of weighing yourself in an accelerating elevator. When does an elevator accelerate upwards? When does an elevator accelerate downwards?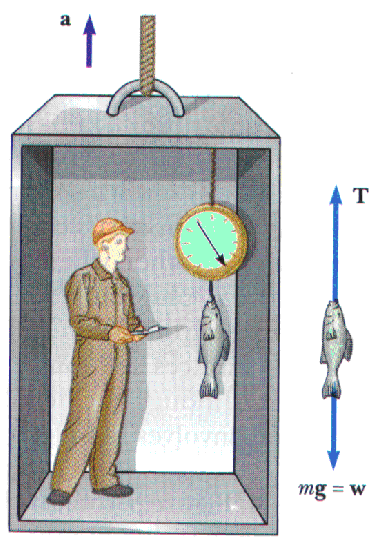
The forces acting on the fish are shown in the free-body diagram. T is the tension supplied by the scale. This is the value the scale reads. We may call it the apparent weight of the fish. The net force on the fish is
Fnet = T - w or
Fnet = T - m g The net force is (always!) equal to the mass times the acceleration. This fish is moving along with the elevator. In this diagram we have taken the acceleration to be up so it is positive.
Fnet = T - m g = m a T = m g+ m a
T = m (g + a)
While the elevator accelerates upward, the apparent weight of the fish is greater than its true weight, mg.
What happens as the elevator accelerates downward?
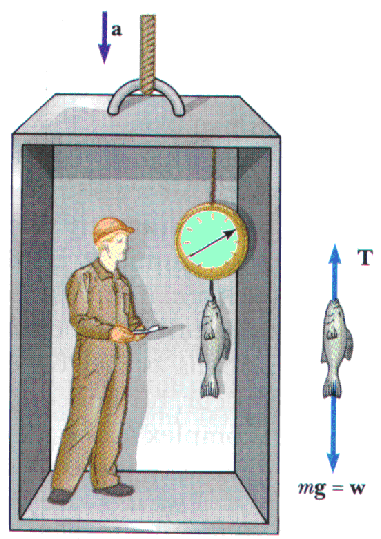
The forces on the fish are again shown in the free-body diagram,
Fnet = T - w or
Fnet = T - mg The net force is (always!) equal to the mass times the acceleration. This fish is moving along with the elevator. Now the acceleration to be up so it is negative.
Fnet = T - m g = m ( - a ) T = m g - m a
T = m (g - a)
While the elevator accelerates downward, the apparent weight of the fish is less than its true weight, mg.
Try this yourself on an elevator -- not weighing a fish, but paying attention to your own apparent weight!



(c) Doug Davis, 2005; all rights reserved