Equilibrium

We continue with our established pattern of identifying all the forces, making a clear "free body diagram", and applying Newton's Second Law,

F = m a

For bodies at rest -- we say they are in equilibrium, we know the acceleration. It is zero. If a = 0 then we know F = 0. Remember, tho', force is a vector. So saying

F = 0

really means

F_x = 0

and

F_y = 0

 

Example: Consider a lamp hanging from a chain. What is the tension in the chain?

As always, begin with a "free body diagram". Tension T acts upward on the lamp while the force of gravity pulls down with force w, the weight of the lamp. The net force is the vector sum of these two forces. The lamp is not accelerating so the force up must equal the force down. In terms of magnitudes, this means

T = w

---

Tension: Tension is the magnitude of the force exerted by a chain or a rope or a string. The direction of that force depends upon the rest of the situation and the object that we are concentrating on at the moment. If we concentrate on the chain shown below, the downward force T' is the force exerted on the chain by the lamp while the upward force T'' is the force exerted on the chain by the ceiling. There is no substitute for good free-body diagrams.

---

Example: Consider a traffic light suspended by cords as shown in the sketch below. What is the tension in each of those cords?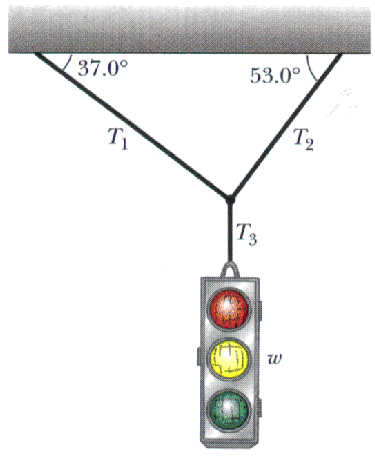

Tension T₃ is easy so we will look at the first. As we have seen in the previous two examples; this tension in a vertical cord supporting a weight is just equal to the weight. In the diagram below, we have drawn in the forces acting on the traffic light. The only forces acting on the traffic light are w, the weight acting downward, and T₃, the upward force due to the vertical cable. T₃ is the tension in this cable. Clearly

T₃ = w

But what of the tensions in the other two cables, T₂ and T₁? To find those, we must look at the junction where the three cables come together. That junction is in equilibrium so

F_net = 0

F_net = F = T₁ + T₂ + T₃ = 0

However, we must remember that this single vector equation is elegant, shorthand notation for two scalar equations,

F_net,x = F _x = T_{1 x} + T_{2 x} + T_{3 x} = 0

F_net,y = F _y = T_{1 y} + T_{2 y} + T_{3 y} = 0

So we must resolve all these forces into their x- and y-components,

T_1x = - T₁ cos 37^o = - 0.8 T₁

T_1y = T₁ sin 37^o = 0.6 T₁

T_2x = T₂ cos 53^o = 0.6 T₂

T_2y = T₂ sin 53^o = 0.8 T₂

T_3x = 0

T_3y = - T₃ = - w

The signs are important! Now we can go back to the component equations and solve for tension T₁ and T₂.

F_net,x = F _x = T_{1 x} + T_{2 x} + T_{3 x} = 0

T_{1 x} + T_{2 x} + T_{3 x} = 0

- 0.8 T₁ + 0.6 T₂ + 0 = 0

T₁ = 0.75 T₂

F_net,y = F _y = T_{1 y} + T_{2 y} + T_{3 y} = 0

T_{1 y} + T_{2 y} + T_{3 y} = 0

0.6 T₁ + 0.8 T₂2 - w = 0

0.6 T₁ + 0.8 T₂ = w

0.6 (0.75 T₂) + 0.8 T₂ = w

1.25 T₂ = w

T₂ = 0.8 w

T₁ = 0.75 (0.8 w)

T₁ = 0.6 w

Strings & Springs			Connected
Return to ToC, Ch 6, Application of Newton's Laws

(c) Doug Davis, 2005; all rights reserved