

Heat Engines, Entropy, & the Second Law
Carnot Engine The Carnot engine -- or the Carnot cycle -- is important because it describes a heat engine that uses reversible processes that can be handled theoretically.
The efficiency of a Carnot engine -- or any reversible heat engine -- is the greatest that is possible to achieve. Call the efficiency of the Carnot engine ec. Then suppose the efficiency of some real heat engine, er, is greater than that of the Carnot engine,
er > ec Then we could use the real heat engine to power a Carnot cycle heat pump. If er > ec, then the net result would be the transfer of heat from a cold temperature to a high temperature. But this violates the Second Law.
Qh is the heat absorbed from the high temperature by the real heat engine and Qh' is the heat expelled to the high temperature by the Carnot cycle heat pump. For this analysis, both Qh and Qh' are intrinsicly positive.
er > ec W/Qh > W/Qh'
1/Qh > 1/Qh'
Qh < Qh'
Qh' > Qh
Qh,net = Qh' - Qh
Qh,net > 0
Since we believe the Second Law, that means our assumption that er > ec is wrong.
A Carnot engine -- or a Carnot cycle -- is a combination of isothermal expansions and compressions and adiabatic expansions and compressions.
A Carnot engine -- or a Carnot cycle -- is a combination of isothermal expansions and compressions and adiabatic expansions and compressions.
From an initial stat A, the gas is placed in contact with the hot temperature reservoir (Th) and expands isothermally (keeping T = Th = constant) to some state B. During this isothermal expansion heat Qh flows into the gas from the hot temperature Th.
From state B, the gas undergoes an adiabatic expansion to state C. No heat is exchanged during this expansion. Expanding an insulated gas means work is done at the "expense" of the internal energy. That means the gas will have a lower temperature. This is the cold temperature Tc.
At state C, we place the gas in contact with the cold temperature heat reservoir (like a large tank of water) and do an isothermal compression to state D. In compressing the gas, work is done on the gas by the outside. But the temperature remains constant -- meaning the internal energy U of the gas remains constant. For this to happen, heat Qc is given out to the cold temperature heat reservoir.
From state D we do an adiabatic compression back to state A. Remember, "adiabatic" means insulated so there is no heat exchange.
These processes may be seen in the drawings of the gas and piston or on the PV diagram immediately above. It will be useful to go back and forth between the two diagrams and the words describing them.
We already know the efficiency of a heat engine,
It can be shown that the ratio of the heat expended to the heat absorbed, Qc/Qh, is also equal to the ratio of the cold temperature to the hot temperature, Tc/Th. Then the efficiency of a Carnot engine can also be written as
The significance of this is that all Carnot engines operating between the same temperatures have the same efficiency. It also shows us that the only way to have an efficiency of 100% is if the cold temperature Tc is absolute zero -- that is, Tc = 0 K. For most practical situations the cold temperature is around room temperature. So increasing efficiency usually means increasing the hot temperature Th. That is why most fuel-efficient automobile engines run hotter than most poorly efficient automobile engines. The efficiency of a real engine will always be less than the efficiency of a Carnot engine running betwen the same temperatures. 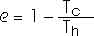
Return to ToC (c) Doug Davis, 2002; all rights reserved