Rocket Propulsion

Rockets provide a wonderful example of Momentum Conservation. As momentum in one direction is given to the rocket's exhaust gases, momentum in the other direction is given to the rocket itself.

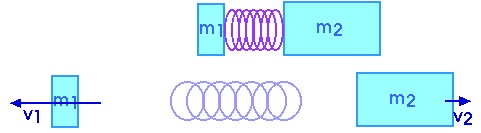
First, think of two masses connected by a lightweight (massless!) compressed spring. When the two spring apart, conservation of momentum tells us the Center of Mass remains where it was (or moving as it was).

P_Tot,i = p_1i + p_2i = 0 + 0 = 0

P_Tot,f = p_1f + p_2f = P_Tot,i = 0

p_1f + p_2f = - m₁ v_1f + m₂ v_2f = 0

m₁ v_1f = - m₂ v_2f

A rocket does much the same thing. Momentum is given to the exhaust gases in one direction so the rocket itself must gain momentum in the other direction. Instead of sending out a single chunk of mass, the rocket fuel is burned continuously. "Continuously" is a code word meaning "use calculus here".

The results are

v_f = v_i + v_exh ln [ M_i / M_f ]

and

Thrust = v_exh [ dM / dt ]

Now, for the details, . . .

---

Consider a rocket initially moving with velocity v and having mass M + dm. The rocket engine burns rocket fuel which leave with an exhaust speed of v_e. During a short amount of time dt, the rocket engine burns an amount of fuel |dm|.

(The sign of dm is important and is often the cause of some concern and confusion).

The initial momentum of the rocket and fuel is

P_init = (m + |dm|)(v)

P_init = m v + |dm| v

After the amount of fuel |dm| is burned the rocket increases its velocity to v + dv and its mass decreases to m so the final momentum of the rocket and fuel is

P_final = (m)(v + dv) + (|dm|)(v - v_e)

P_final = m v + m dv + |dm| v - |dm| v_e

We expect the total momentum of "the system" to remain constant,

P_final = P_init

m v + m dv + |dm| v - |dm| v_e = m v + |dm| v

m v + m dv + |dm| v - |dm| v_e = m v + |dm| v

m dv - |dm| v_e = 0

The mass is decreasing so the change in mass dm is intrinsicly negative, dm < 0.

m dv + dm v_e = 0

m dv = - v_e dm

dv = - v_e [ dm/m ]

Now we need to integrate this; remember v_e, the exhaust speed, is a constant.

Remember, M_i > M_f so the natural log will be positive. Of course, we would expect that since we also expect v_f > v_i.

Center of Mass			Summary
Return to ToC, Ch9, Linear Momentum

(c) Doug Davis, 2001; all rights reserved