Uncertainties

This wave aspect of nature has a rather surprising effect on the basic ideas underlying measurements. The figure here shows particles -- they could be photons or electrons or anything else -- incident upon a screen with a single slit of width y. This is the same as the single slit diffraction we discussed in Optics where the slit width was labeled D. After a particle passes through this slit we can not predict just where it will strike the screen. It has a large probability of being within the large central maximum between the two minima as shown in the sketch. After passing through the slit of widthy the particle has some momentum in the vertical direction p_y. The slit determines the particle's vertical position to within an uncertainty of y, the width of the slit. As it emerges from the slit, the particle's vertical momentum is uncertain to within p_y. In our present context means a spread in values or an uncertainty in a value. This is not an uncertainty due to lack of accuracy. The word "indeterminancy" is sometimes used here to indicate that the position or momentum -- by the basic character of Nature -- can not both be determined with infinite precision.

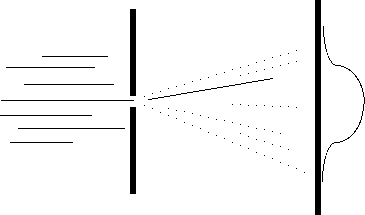
As you have already seen in Chapter 25 concerning light, the angle between the bright central maximum and the first dark minimum is

sin = /y

for small angles , sin is nearly equal to tan so

y = / tan

The deBroglie wavelength is

= h / p = h / p_x

The tangent of the angle is

tan = p_y / p_x

Therefore,

y = [ h / p_x] [ p_x / p_y ] = h / p_y

or

(y) (p_y) = h

As the slit width y is made smaller, the angle of the central maximum increases. The slit width y is the uncertainty in the vertical position of the particle. As the width of the central maximum increases, there is greater p_y in the vertical momentum of the particle.

(y) (p_y) = h

is known as Heisenberg's uncertainty principle. It is far more basic or foundational than just this application to particles passing through a single slit.

Every measurement affects the object being measured. We may shine a light on a baseball and measure its location without any apparent disturbance of the baseball. But if we shine photons -- or even a single photon -- on an electron to measure its location we disturb that electron. By measuring its position, we disturb its momentum. The more accurately its position is measured the more uncertain will be its momentum. There are similar equations expressing Heisenberg's uncertainty principle for all three components of position and velocity,

(x) (p_x) = h

(y) (p_y) = h

(z) (p_z) = h

As with the deBroglie wavelengths of macro objects, Planck's constant h is so small that we never observe the consequences of the uncertainty principle for macro objects. But it is very real for tiny particles.

---

The velocity of a 0.150 kg baseball is measured to be 22.50 m/s with an accuracy of 0.01%.

How accurately can its position be determined?

To solve this, we need to apply Heisenberg's uncertainty principle.

Solution: First, we find the uncertainty in the momentum,

p_x = 0.0001 p_x = (0.0001)(0.150 kg)(22.50 m/s)

p_x = 0.00034 kg m/s

Now we can apply Heisenberg's uncertainty principle',

(x) (p_x) = h

and solve for the uncertainty in position x,

x = h / p_x

x =

x = 1.96 x 10 ^{- 30} m

This is immeasurably small.

---

The velocity of a 20 keV electron is measured to an accuracy of 0.01%.

How accurately can its position be determined?

Again, we will need to apply Heisenberg's uncertainty principle. But first we must find the uncertainty in the momentum. We know the kinetic energy of the electron and can solve that for the speed v. We will then use that to find the momentum and the uncertainty in the momentum and, finally, we will use the Heisenberg uncertainty principle.

Solution: From the kinetic energy,

KE = (¹/₂) mv² = 20 keV

we can solve for the speed

v² = 2 KE / m = [40 keV / 9.11 x 10 ^{- 31} kg] [^{1000 ev}/_keV] [1.6 x 10 ^{- 19} J / eV] [(kg m/s²) / J]

or

v² = 7.025 m²/s²

v = 8.38 x 10⁷ m/s

We can use this to find the momentum

p_x = m v_x = (9.11 x 10 ^{- 31} kg)(8.38 x 10⁷ m/s)

p_x = 7.64 x 10 ^{- 23} kg m/s

The uncertainty in the momentum is 0.01% of the momentum,

p_x = (0.01%) p_x

p_x =7.64 x 10 ^{- 27} kg m/s

Now we can use the Heisenberg uncertainty principle,

(x) (p_x) = h

and solve for the uncertainty in the position, x,

x = h / p_x

x =

x = 8.7 x 10 ^{- 8} m

This is no longer immeasurably small. This is reasonably large on the scale of atomic dimensions. An atomic diameter is about 10^-10 m so this is an uncertainty in an electron's position of about a thousand atomic diameters.

Probabilities			More Results
Return to Ch 28, Quantum Mechanics

(c) Doug Davis, 2002; all rights reserved