PHY 1150

Chapter 5, Circular Motion and Gravity

5.1 A horse moves with a tangential speed of 1.9 m/s when it is 8.5 m from the center of a carousel. Calculate its centripetal acceleration. If a 70-kg person sits on the horse, what is the net force on the rider?

a_c = v²/r = = 0.42 m/s²
F_c = m ( v²/r ) = ( 70 kg ) ( 0.42 m/s² ) = 29.7 N

5.6 A coin sits 15.0 cm from the center of a variable-speed turntable. The coin remains in place as the speed of the turntable increases until it reaches a rate of 2 revolutions per second and then it starts to slide. What is the coefficient of friction between the coin and the surface?
Remember, we have changed the angular speed from 60 to 2 revolutions per second to make this a more reasonable question.

First, find the linear speed coin and its centripetal accleration.

To have this acceleration, the net force must be

Since we do not know the mass of the coin, we will put into the equation simply as “m” and expect that it will later “drop out”.

Now apply F = m a

Fy = m ay	and	Fx = m ax
Fy = FN - mg = 0		- Ff = - m v2 / r
FN = mg		Ff = µ FN
		- µ FN = - m v2 / r
		µ FN = m v2 / r
		µ mg = m v2 / r
		µ g = v 2 / r
		µ = v 2 / g r
		µ = (188.5 cm/s)2 / [(980 cm/s2)(15 cm)]
		µ = 2.41

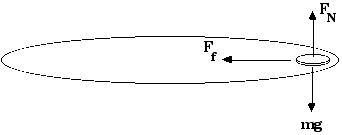
µ = 2.41 is a fairly large coefficient of friction; that is, there must be rubber or something like that on the bottom of the coin.

5.10 A 1200-kg car makes a curve on a flat road of radius 60 m at a speed of 15 m/s. Will the car be able to make the turn if

a) the pavement is dry and has a coefficient of friction of 0.65?
b) there is oil on the pavement and the coefficient of friction is only 0.20?

The free body diagram for this looks much like the free body diagram for problem 5.9 above. The friction force must provide the centripetal acceleration. Being on a flat curve, the normal force happens to equal the weight; F_N = m g .
Now apply F = m a

Fy = m ay	and	Fx = m ax
Fy = FN - mg = 0		- Ff = - m v2 / r
FN = mg		- µ FN = - m v2 / r
		µ FN = m v2 / r
		µ mg = m v2 / r
		µ g = v2 / r
		µ = v2 / g r
		µ = (15 m/s)2 / [(9.80 m/s2)(60 m)]
		µ = 0.38

µ = 0.38 is the minimum value of the coefficient of friction that is necessary to provide enough friction force to equal the centripetal force required to allow the car to make the curve.

Therefore, . . .

a) Yes, the car can make the curve when µ =0.65.
b) No, the car will not make the curve when µ = 0.20.

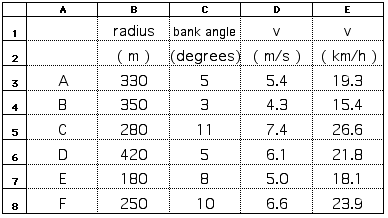
5.21 The table below lists data for six banked highway curves-giving the radius of each curve and the angle at which the curve is banked. Find the maximum speed at which these curves may be traveled without depending upon friction and rank them from slowest to fastest

For calculations that are going to be repeated, it is best to solve the problem symbolically once and then plug particular values into the resulting solution. A spreadsheet is a convenient way to carry out this final calculation.
We already know

tan = v² / r

or

v² = r tan

5.24 A 60-kg pilot comes out of a dive by flying along an arc of radius 800 m with a speed at the bottom of 120 km/h. What is her apparent weight?

v = 120 km/hr [1000 m/km] [hr/3600 s] = 33.3 m/s

5.30 A car of mass 1000 kg goes over the crest of a hill whose radius of curvature is 40 m measured in a vertical plane.

(a) What is the force of the car on the road surface if the car’s speed is 15 m/s?
(b) Calculate the magnitude and direction of the necessary force between car and road if the speed at the top of the crest is 20 m/s. Explain your answer.

a) v = 15 m/s

F_N = (1000 kg) [ (9.8 m/s²) - ]
F_N = (1000 kg) [ 9.8 - 5.6 ] m/s²
F_N = (1000 kg) [4.2 ] m/s²
F_N = 4,200 N = 4.2 kN

b) v = 20 m/s

Of course, the road can not exert a negative (meaning downward) normal force. Therefore, the car looses contact with the road!


5.34 In the ROTOR ride on a midway, passengers are pressed against the inside vertical wall of a rotating drum 2.5 m in radius. This drum takes 2.0 seconds to make a complete rotation; that is, it rotates at 30 rpm (revolutions/minute).

(Six Flags - St Louis - has this ride and there it is known as "Tom's Twister". Take a look at it this summer -- as participant or as observer!)

(a) Viewed from an Earth-based frame of reference outside the drum, what are the magnitude and direction of the force of the wall on a rider whose mass is 70 kg?
Initially the rider’s weight is supported by the floor. After the ROTOR is at full speed the floor is removed.
(b) If the coefficient of static friction between the passenger and the wall is 0.6, will the passenger slip or be held pressed against the vertical wall?
(c) Describe the situations -- including the forces -- from the reference frame of the passenger.

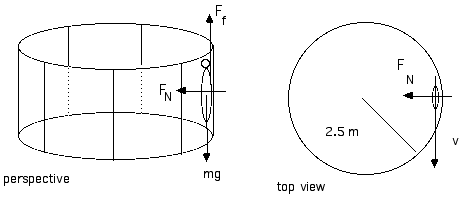
The normal force, F_N, provides the centripetal force, F_c = m v² / r.

v = = = = 7.8 m/s

F_N = F_c = m = (70 kg) = 1,730 N

For comparison, the rider’s weight is

so the normal force is about two and a half times as large. The normal force is directed inward, toward the center of the circle.

Now the floor of the ROTOR is moved down and the friction force, pointing up, must equal the weight, pointing down, to keep the rider from sliding down along with the floor.
The maximum value of the friction force is

The maximum friction force is greater than the weight. Therefore, the actual friction force will just equal the weight and the passenger will remain in place on the wall of the ROTOR.

From inside the ROTOR, from the noninertial reference frame, the passenger will feel pushed to the outside by a “centrifugal force” to which the wall responds with the normal force. Because there is a normal force, there can be a friction force and all the rest is the same.

5.41 Calculate the mass of Jupiter, given that its moon Callisto has a mean orbital radius of 1.88 x 10⁶ km and an orbital period of 16 days, 16.54 hours.

The force of gravity provides the centripetal force to keep Callisto in its orbit.

F_g = G M_J m / r² = m v² / r = F_c
M_J =

We must find the linear speed of Callisto.

v =

T = 16 d, 16.54 h = [(16)(24) + 16.54 ] h = 400.54 h
T = 400.54 h [3600 s/h] = 1.44 x 10⁶ s

F_gravity = F_centripetal

F_gravity = G M_J m_C/r² = m_C v²/r = F_centripetal

G M_J m_C/r² = m_C v²/r

M_J = r v²/G

M_J = 1.9 x 10²⁷ kg

5.44 Starting with the moon's period of 27.3 days, calculate the radius of its orbit.

The gravitational force between Earth and our moon provides the centripetal force,

F_g = = m = F_c
= m

Don’t try to solve for the radius immediately for we know the velocity only in terms of the radius,

v =
= =

= m = m

T = 27.3 da (24 h/da) (3600 s/h) = 2.36 x 10⁶ s
r³ =
r³ =
r³ = 5.627 x 10²⁵ m³
r = 3.83 x 10⁸ m
r = 3.83 x 10⁵ km

5.47 The acceleration of a falling body near Earth’s surface, at a distance R from Earth’s center, is 9.80 m/s².

(a) Use a suitable proportion to calculate the acceleration toward Earth of a falling body that is 60 R from Earth’s center.
(b) Our moon is in an orbit of radius 60 R, with a period of revolution of 27.26 days. Show, as did Sir Isaac Newton, that the centripetal acceleration of the moon toward Earth agrees with your answer from part (a).

Earth’s radius is R = 6.38 x 10³ km.

F = G
m g = G
a(R) = g = G
a(60R) = G = G = g
a(60R) = g = (9.8 ) = 2.7 x 10^-3 = 2.7

a_c =
v = = = =
v = 1,020 m/s
a_c = = = = 2.7 x 10^-3 = 2.7

5.49 What orbital radius should a weather satellite have if it is to have a period of 6.0 hours?

F_c = m = G m = F_g
= G
v = =
= = G
r³ = G M_E T²
r³ = (6.67 x 10^-11) ( 5.98 x 10²⁴) (6.0 h )²
r³ = 4.71 x 10²¹

r = 1.68 x 10⁷ m = 1.68 x 10⁴ km = 16,800 km

5.60 From the data in Table 5.1, calculate the acceleration of free fall on the surface of

a) Jupiter,
b) Saturn, and
c) our Moon. F = m a = G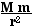

a = G

a)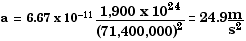

b)

c)

 

| ToC, Chapter 5 | Course Calendar |

 

(C) 2002, Doug Davis; all rights reserved