Newton's Laws of Motion

Applications

Now that we know Newton's Laws of Motion, how do we apply them? How can they let us predict the motion of an object if we know all the forces acting upon it? How can they let us predict the forces on an object if we know its motion?

It is only a slight over statement to say that the rest of this course is just looking for devious ways to apply
F = m a

Example 1: Consider a crate being pulled along a frictionless floor (while such a floor is very hard to find, this will still help us understand the concept and we can return to this situation later, after considering friction, and solve it more realistically).

Consider a crate being pulled along a horizontal, frictionless floor. A rope is tied around it and a man pulls on the rope with a force of T. T is the tension in the rope. What happens to the crate?

Before we can apply Newton's Second Law,
F = m a
we must find the net force -- the vector sum of all the forces -- acting on the object. In addition to the force T exerted by the rope, what other forces act on the object?

As discussed in class, in Mechanics, we can restrict our attention to "contact" forces and "gravity". That means gravity pulls down on this crate with a force equal to its weight, w. But the floor supports the crate. The floor responds by pushing up on the crate with a force we call the normal force. "Normal" means "perpendicular". We will call this force n; you may also encounter it labeled N or F_N.

These forces are shown on the "free body diagram" above. We have drawn in all the forces acting on the object. The net force is the vector sum of these forces.
F_net = F = T + n + w
where , the Greek upper case "sigma", means "the sum of". Remember, tho', vector notation is always elegant shorthand notation. When we write
F_net = F = T + n + w
we have really written
F_{net, x} = F_x = T_x + n _x + w _x
and
F_net,y = F _y = T _y + n _y+ w _y
What are these x- and y-components of the forces T, n, and w? For this first, simple example, we can find -- by inspection -- that these components are
T_x = T
T _y = 0

n_x = 0

n _y = n

w_x = 0

w _y = - w

Now we are ready to apply
F = m a
But that must first be written in terms of components,
F_x = F_net,x = F_x = m a_x
F_x = F_net,x = F_x = T_x + n_x + w_x = T = m a_x

T = m a_x

a_x = T / m

The crate has a horizontal acceleration equal to the tension T divided by m, the mass of the crate. What about the forces in the vertical direction?
F_y = F_net,y = F_y = m a_y
F_y = F_net,y = F_y = T_y + n_y + w_y = n - w = m a_y

n - w = m a_y

Since we know the crate does not accelerate in the y-direction -- it does not jump up off the floor and it does not burrow down into the floor -- we know a_y = 0, so
n = w
The upward normal force exerted by the floor on the crate, in this situation, is equal to the weight, the downward force of gravity.

Example 2: What are the forces acting on book if you push down on it with a force F while it sits on a smooth, horizontal table as shown in the sketch below?

Draw in all the forces. This is called a "free body diagram". We will restrict ourselves, in this Mechanics course, to "contact forces" and the force of gravity. Contact forces, for this case, will be the "normal" force -- the perpendicular force -- exerted by the table -- labeled n in the diagram -- and the force F exerted by the hand. Gravity exerts a force downward, called the weight and labeled w. Just as in the previous example, we can immediately write
F = m a
but that is really elegant shorthand for
F_x = F_net,x = F_x = m a_x
and
F_y = F_net,y = F_y = m a_y
In this example, tho', nothing happens in the horizontal direction. All of the forces have only vertical components so all we really have is
F_y = F_net,y = F_y = m a_y
Taking up as positive, we have
F_y = F_net,y = F_y = n - w - F
Since the book sits on a table, we know it does not accelerate so a_y = 0. This means
n - w - F = 0
n = w + F

We can use Newton's Laws to determin the value of the normal force n.

This same idea and technique can be used is slightly different situation,

Example 3: Consider a lamp hanging from a chain. What is the tension in the chain?

As always, begin with a "free body diagram". Tension T acts upward on the lamp while the force of gravity pulls down with force w, the weight of the lamp. The net force is the vector sum of these two forces. The lamp is not accelerating so the force up must equal the force down. In terms of magnitudes, this means
T = w

Tension: Tension is the magnitude of the force exerted by a chain or a rope or a string. The direction of that force depends upon the rest of the situation and the object that we are concentrating on at the moment. If we concentrate on the chain shown below, the downward force T' is the force exerted on the chain by the lamp while the upward force T'' is the force exerted on the chain by the ceiling. There is no substitute for good free-body diagrams.

Example 4: Consider a traffic light suspended by cords as shown in the sketch below. What is the tension in each of those cords?

Tension T₃ is easy so we will look at the first. As we have seen in the previous two examples; this tension in a vertical cord supporting a weight is just equal to the weight. In the diagram below, we have drawn in the forces acting on the traffic light. The only forces acting on the traffic light are w, the weight acting downward, and T₃, the upward force due to the vertical cable. T₃ is the tension in this cable. Clearly
T₃ = w

But what of the tensions in the other two cables, T₂ and T₁? To find those, we must look at the junction where the three cables come together. That junction is in equilibrium so
Fnet = 0
F_net = F = T₁ + T₂ + T₃ = 0

However, we must remember that this single vector equation is elegant, shorthand notation for two scalar equations,
F_net,x = F _x = T_{1 x} + T_{2 x} + T_{3 x} = 0
F_net,y = F _y = T_{1 y} + T_{2 y} + T_{3 y} = 0

So we must resolve all these forces into their x- and y-components,
T_1x = - T₁ cos 37^o = - 0.8 T₁
T_1y = T₁ sin 37^o = 0.6 T₁

T_2x = T₂ cos 53^o = 0.6 T₂

T_2y = T₂ sin 53^o = 0.8 T₂

T_3x = 0

T_3y = - T₃ = - w

The signs are important! Now we can go back to the component equations and solve for tension T₁ and T₂.
F_net,x = F _x = T_{1 x} + T_{2 x} + T_{3 x} = 0
T_{1 x} + T_{2 x} + T_{3 x} = 0

- 0.8 T₁ + 0.6 T₂ + 0 = 0

T₁ = 0.75 T₂

F_net,y = F _y = T_{1 y} + T_{2 y} + T_{3 y} = 0

T_{1 y} + T_{2 y} + T_{3 y} = 0

0.6 T₁ + 0.8 T₂2 - w = 0

0.6 T₁ + 0.8 T₂ = w

0.6 (0.75 T₂) + 0.8 T₂ = w

1.25 T₂ = w

T₂ = 0.8 w

T₁ = 0.75 (0.8 w)

T₁ = 0.6 w

Now we expand our applications and look at an Atwoods Machine

Example 5: Consider the Atwoods Machine shown here with masses m₁ and m₂. They are attached by a lightweight cord over a pulley as shown. What is the acceleration of the system?

We may say "acceleration of the system" for masses 1 and 2 will have the same acceleration since they are attached by a cord.

If m₂ > m₁ and the Atwoods machine is released from rest, mass m₁ will accelerate upward while mass m₂ accelerates downward. Actually, that will be their accelerations whether the system is released from rest or is moving. It is probably easier to visualize if you think of the system being released from rest.

How can we apply F = m a ?

We apply F = m a to the masses, one at a time.

Look at the smaller mass, m₁. What are the forces acting on this mass?

The tension in the string exerts a force up while gravity exerts a force down. We expect this mass to have an acceleration a that is up. There are no horizontal forces.

We will take up as positive.
F_net = F = T - w₁ = m₁ a
F_net = F = T - m₁ g = m₁ a

T - m₁ g = m₁ a

This one equation has two unknowns -- tension T and acceleration a. So we need more inormation.

We get that additional information by looking at the forces acting on the heavier mass, m₂, and applying Newton's Second Law, F = m a, to that mass. There are no horizontal forces.

The tension in the string exerts a force up while gravity exerts a force down. We expect this mass to have an acceleration a that is down. We can choose to call down "positive" for this mass or we can call up "positive" and then we expect this mass to have an acceleration of - a. Either choice is fine.

This time, let's choose down as "positive".
F_net = F = w₂ - T = m₂ a
F_net = F = m₂ g - T = m₂ a

m₂ g - T = m₂ a

Of course, this one equation also has two unknowns -- tension T and acceleration a.

But now we have two equations with two unknowns and that is sufficient. We can solve for the tension T in the first equation,
T - m₁ g = m₁ a
T = m₁ g + m₁ a

and then stubstitute that into the second equation
m₂ g - T = m₂ a
m₂ g - ( m₁ g + m₁ a ) = m₂ a

m₂ g - m₁ g - m₁ a = m₂ a

m₂ g - m₁ g = m₁ a + m₂ a

( m₂ - m₁ ) g = ( m₁ + m₂ ) a

( m₁ + m₂ ) a = ( m₂ - m₁ ) g

a = ( m₂ - m₁ ) g / ( m₁ + m₂ )

Example 6: Now, let's consider an inclined Atwoods machine. Masses m₁ and m₂ are connected by a string which runs over a pulley and mass m₂ sits on a smooth inclined plane. Remember, "smooth" is just a code word for "frictionless"; we'll get to friction shortly. This inclined Atwoods machine is sketched here:

Now we want to apply Newton's Second Law, F = m a. Newton's Second Law describes the effect of forces on one object. So we must isolate all the forces on mass m₁ and apply it. Then we isolate all the forces on mass m₂ and apply it again. This calls for good free-body diagrams.

The hanging mass m1 has only two forces on it; the string pulls up with a force we label T while gravity pulls down with a force we label w:

We expect the acceleration to be upward and have that drawn beside the free-body diagram. As always, we are now ready to apply F = m a to these forces acting on this object.
F_net = F = T - m₁ g = m ₁ a
T - m₁ g = m ₁ a

As we might expect by now, this one equation has two unknowns -- tension T and acceleration a -- so we must look elsewhere for additional information. Of course, the place to look is at the other mass.

Carefully construct a free-body diagram showing all the forces acting on mass m₂. There are three forces acting on this mass -- the string exerts a force T, the (frictionless) inclined plane exerts a "normal" force n, and gravity pulls down with a force of w₁ = m₁ g. To find the net force, we must resolve these vectors into their components. Since the acceleration will be along the direction of the plane, we have chosen that direction as the x-axis.

Notice that the angle in this diagram is measured from the y-axis. That means the weight has components of
w_x = m₂ g sin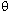
w_y = - m₂ g cos

And we have
n_x = 0
n_y = n

and

T_x = - T

T_y = 0

Make sure you understand the signs and sines! Do not go on until all these components are clear to you!

Now we can apply Newton's Second Law to this mass:
F = m a
F = F_net = T + n + w = m a

F_x = F_net,x = F_x = m ₂ a_x

F_x = T _x+ n _x+ w _x = m ₂ a_x

- T + 0+ m₂ g sin = m ₂ a_x = m ₂a

where we have used
a_x = a
since the acceleration is only in the positive x-direction.
- T + m₂ g sin = m₂a
This provides all the information we need to solve for T and a. As before, we can solve one of these equations for T and substitute that into the other equation and solve for a.
T = m₂ g sin - m₂a
[m₂ g sin - m₂a] - m₁ g = m ₁ a

m ₁ a + m₂a = m₂ g sin - m₁ g

( m ₁ + m₂) a = ( m₂ sin - m₁ ) g

a = ( m₂ sin - m₁ ) g / ( m ₁ + m₂)

What about the y-components of the forces on mass m₂, on the inclined plane?
F_y = F_net,y = F_y = m ₂a_y
F_y = T _y+ n _y+ w _y = m ₂ a_y = 0

where we have used
a_y = o
since the acceleration is only in the positive x-direction and there is no acceleration perpendicular to the plane.
T _y+ n _y+ w _y = 0
0 + n - m₂ g cos = 0

n = m₂ g cos

From the y-components of the forces on mass m₂, we can solve for the normal force. This will be important when we take friction into account.

Example 7: Two blocks of masses m₁ and m₂ are placed in contact with each other on a smooth, horizontal plane as shown here. A constant horizontal force F is applied to m₁. What is the acceleration of each mass?

In one sense, we can (almost) solve this example intuitively -- in our head. A force F is applied to an object whose mass is m = m₁ + m₂. So its acceleration must be
a = F / m
or
a = F / (m₁ + m₂)
That's the right answer! But is there nothing more to this question? Simple questions -- the intuitively obvious kind -- make wonderful templates or examples for more difficult problems.

Look at all the forces on m₁. Make a good free-body diagram of the forces acting on m₁.

Of course the external force F pushes to the right on the mass m₁. Gravity pulls down with force w₁ = m₁ g and the plane responds with a normal force n₁. But the other mass -- m₂ -- exerts a force on mass m₁. This force is labeled P' and points to the left. We can apply Newton's Second Law to the y-component forces and find that n₁ = w₁1. But now there is an additional and unknown force in the x-component of Newton's Second Law,
F_1,net = F - P' = m₁ a
We need more information so we turn to the other mass, m₂

The first mass m1 exerts a force P on this mass, m2. Applying the y-component of F = m a, we readily find
n₂ = w₂
For the x-components, the only force acting on m2 is P so
F_2,net = P = m₂ a
However, from Newton's Third Law, F₁₂ = - F₂₁, we know that P = P' so
F - P' = m₁ a
F - m₂ a = m₁ a

F = m₁ a + m₂ a

F = ( m₁ + m₂) a

a = F / ( m₁ + m₂)

That is the same answer we found so quickly earlier but this may provide a pattern to use for more complex situations.

Example 8: This particular example is stated in terms of weighing a fish in an accelerating elevator. It is also fun to think of weighing yourself in an accelerating elevator. When does an elevator accelerate upwards? When does an elevator accelerate downwards?

The forces acting on the fish are shown in the free-body diagram. T is the tension supplied by the scale. This is the value the scale reads. We may call it the apparent weight of the fish. The net force on the fish is
F_net = T - w
or
F_net = T - mg
The net force is (always!) equal to the mass times the acceleration. This fish is moving along with the elevator. In this diagram we have taken the acceleration to be up so it is positive.
F_net = T - m g = m a
T = m g+ m a

T = m (g + a)

While the elevator accelerates upward, the apparent weight of the fish is greater than its true weight, mg.

What happens as the elevator accelerates downward?

The forces on the fish are again shown in the free-body diagram,
F_net = T - w
or
F_net = T - mg
The net force is (always!) equal to the mass times the acceleration. This fish is moving along with the elevator. Now the acceleration to be up so it is negative.
F_net = T - m g = m ( - a )
T = m g - m a

T = m (g - a)

While the elevator accelerates downward, the apparent weight of the fish is less than its true weight, mg.

Try this yourself on an elevator -- not weighing a fish, put paying attention to your own apparent weight!

Third Law

Friction

Return to ToC, Ch4, Newton's Laws of Motion

(c) 2002, Doug Davis; all rights reserved


Third Law			Friction
Return to ToC, Ch4, Newton's Laws of Motion