2. If    is a well-formed sentences, then  ~ is a well-formed sentence.

Clause 2 is a recursive clause – that means we could take the output of Clause 2, and feed it back in as new input, in order to build bigger and bigger negations.


We will now build a semantic rule for negations as well; and this semantic rule will keep up with Clause 2 at every turn, because (as we will see) this semantic rule for negations will also be recursive.  (It has to be recursive, in order to keep up with recursive Clause 2.)

The semantic rule for negations is very simple: just as the negation "~P" is built up out of "P", the truth value of "~P" will be built up out of the truth value of "P".  So consider a sentence "P", and its negation "~P".


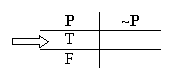
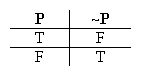
Right away we know from Bivalence that there are only two kinds of situation (two valuations) possible for "P": one where "P" is true, and one where "P" is false:


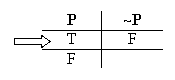
Let's start with the first valuation, where "P" is true.

Suppose "P" stands for some English sentence, like "It's raining."  Then "~P" would mean "It's not raining."  So the first valuation is a situation where "P" is true – a situation where it's true that it's raining.  In that situation, what would the sentence "It's not raining" be?  Obviously: in a situation where it's true that it's raining – a rainy situation – the sentence "It's not raining" would be false.


Next, consider the kind of situation where "P" is false.

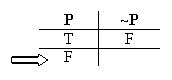
This is the sort of situation where it's false to say "It's raining".  Now, in a situation where it's false that it's raining, what would the sentence "It's not raining" be?  This is just as obvious: In a situation where it's false that it's raining – a non-rainy situation – the sentence "It's not raining" would be true.

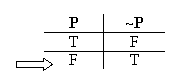
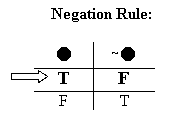
That's basically all there is to the semantic rule for negations.  Of course, the rule applies to all negations, not just "~P".  So we can leave "P" out of it, and state it as a general rule:


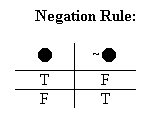
(Like always, the little " " here is just a blank, where we can put in any WFS.)

Now I said a little while back that this semantic rule is recursive – it can take its own output as fresh input.  Let's look at how that would work.

Grammatically, we build up a negation, going from "P" to "~P".


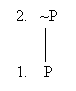
Of course, once we get "~P" as the output of Clause 2, we turn right around and feed "~P" back into Clause 2, as fresh input, and get its negation in turn:


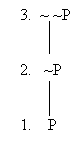
All of that is grammatical old hat to us by now.  But let's look at the semantics of
"~ ~P" as well – let's see when it would be true to say "~ ~P", and when it would be false.

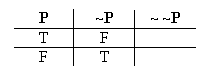
We've already looked at when "P" and "~P" are true, and when they're false:


Now we want to figure out "~ ~P" in turn.


To figure out "~ ~P", we just use the Negation Rule all over again – only now "~P" is the input (the thing getting negated), and "~ ~P" is the output (the negation of that first thing).  That makes sense, after all, because "~ ~P" is the negation of "~P".  So let's feed "~P", and its truth values, into the Negation Rule.

Start with the first valuation.

In the first valuation, "~P" is false.  What will "~ ~P" be in this valuation?  The Negation Rule tells us: if a given sentence is false, its negation will be true.


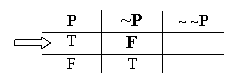
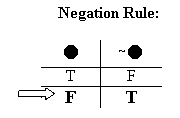
So since "~P" is false in the first valuation, the Negation Rule says "~ ~P" will be true in that valuation.


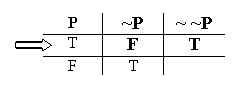
We're half-done.  Now we look at the second valuation.  In the second valuation, "~P" is true.


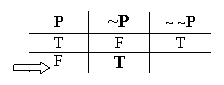
And since "~ ~P" is the negation of "~P", we use the same old Negation Rule to figure out the value of "~ ~P" in this valuation.  The Negation rule says that if a given sentence is true, then the negation of that sentence will be false:


So, since "~P" is true in the second valuation, its negation, "~ ~P", will be false in that second valuation:


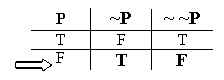
So we've seen exactly what the truth values of "~ ~P" are, in the different situations.  But we've seen something even more important as well: we didn't need one rule for figuring out "~P" from "P", and then an entirely different, second rule for figuring out "~ ~P" from "~P".  Instead, in this second case, we just 'recycled' the same old Negation Rule we used the first time.  That's what I meant about the Negation Rule being recursive: the Negation Rule of our semantics is 'cyclical' just like our recursive rules of grammar, taking its output (the values for "~P") as fresh input, to figure out yet further outputs (the values for "~ ~P").

---

Before we move on, it will be useful to make a couple more points about what we've just done.

The first point is just a point of jargon.  We've been building these little vertical tables of truth values (T's and F's), that give a profile of the truth-and-falsehood behavior of sentences (when these sentences are true, when they're false).  In the last example we looked at, we had three of these little vertical lists: one for "P", one for "~P", and one for "~ ~P".


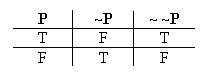
There's a technical name for these little vertical lists of truth values: each such list is called a truth table.  So what we've done in the above example is build three truth tables: one truth table for "P", one for "~P", and one for "~ ~P".

The second point also involves a new piece of logical jargon, but also an important new idea.  If we look at the truth tables for "P" and "~ ~P", we notice that they're exactly the same.


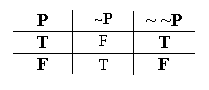
"P" and "~ ~P" are true in the same situations (the first valuation), and false in the same situations (the second valuation); so they have identical truth tables.  When two sentences have exactly the same truth tables like this, we say that the two sentences are truth-functionally equivalent.  As we see from their truth tables, "P" and "~ ~P" are indeed truth-functionally equivalent.

Now, there's an interesting feature of sentences that are truth-functionally equivalent, which we can see by looking at English-language counterparts to "P" and "~ ~P".  Suppose, once again, that "P" stand for the English sentence "It's raining"; then "~ ~P" stands for the English sentence "It's not not raining" (or one of its prettier relatives, such as "It is not the case that it's not raining").  Now, look at those two English sentences.

It's raining
It's not not raining

English speakers naturally look at these sentences and judge that they're both saying the same thing – that the two sentences mean the same thing.  And when we build truth-tables for these sentences (translated into logical notation), we see that they're truth-functionally equivalent.

This illustrates a point – which we will notice again and again below – that truth-functional equivalence is a good test of when two sentences logically mean the same thing.  "It's raining" and "It's not not raining" mean the same thing, logically – and sure enough, their translations are truth-functionally equivalent.  This is what I was hinting at earlier, when I said that we'd start out our semantics from the truth and falsehood end, but (without even trying) make our way back to meaning as well.  Without even trying, our theory of truth and falsehood has fallen backwards into a little test of when two sentences will (logically speaking) mean the same thing.  We will see many more examples of this below.