Grammatical Trees Revisited (and Reversed)
We know that any sentence we build will be a grammatical sentence – a “formal sentence” – as long as we faithfully follow the four grammatical rules of our formal language in building up that sentence. A grammatical tree for a sentence demonstrates that the sentence is grammatical, by showing how every step in the construction of that sentence followed one of the four rules.
So every sentence with a grammatical tree that faithfully follows the four rules of grammar will be a grammatical sentence. But does it work the other way around as well? That is: while every sentence with a tree is a grammatical sentence, will every grammatical sentence have some tree, which demonstrates its grammaticality?
The answer is: yes. Each grammatical sentence in our formal language will have some grammatical tree showing that the sentence is grammatical. In fact, we can make an even stronger claim: each grammatical sentence in our formal language will have one and only one grammatical tree showing that the sentence is grammatical. (In other words: there will never be two different ways of using the four rules of grammar to build a certain sentence in our formal language.)
That means that, even if you didn’t see the sentence being built up – only the final, completed sentence – you can rest assured that there is a particular grammatical tree that could be hung under that sentence, illustrating the grammatical steps involved in building it up.
And that raises a further question: given that there is exactly one grammatical tree for each sentence in our formal language, do we have some technique for figuring out what that tree is, for any given formal sentence? We just said that, even if you only see the whole finished sentence, and didn’t witness which rules were used to build which parts, you can still rest assured that there is a definite tree, showing which rules applied in which order to build up the sentence. But it’s one thing to know, in the abstract, that the formal sentence must have some tree; it quite another thing to be able to spell out exactly what the tree is for a finished sentence, whose construction we didn’t witness. Is there some full-proof procedure for working backwards, from the finished sentence, and reconstructing what its tree must have been?
Again, the answer is: yes. There is indeed a full-proof technique for figuring out the grammatical tree for any given formal sentence. In fact, the technique for building a tree under a completed sentence will be just the reverse of the technique for building up a sentence, step by step, out of sentence letters.
For example, consider this sentence.
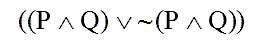
This is indeed a formal sentence – a grammatical sentence in our formal language. We know that there must be a tree we could build under it, illustrating the exact moves needed to build this sentence out of sentence letters, using our three recursive rules. The trick in building the tree under this sentence will, of course, be in figuring out exactly which rules were applied, in which order.
But we have one useful clue, to get the process started: we know what kind of sentence this is. This sentence is a disjunction. And what makes a sentence a disjunction is that its main connective is a vel, “
”.
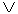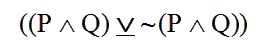
But there’s only one recursive rule that adds a vel to a sentence, and that’s Rule 4 of our grammar.
Rule 4 is the only rule that could have spit out a disjunction as its finished product. Since this sentence is a disjunction, the final, finished sentence must be the handiwork of Rule 4.
Now, Rule 4 takes two smaller formal sentences as inputs, puts a vel between them, and wraps the whole thing in parentheses. So we know that, as the output of Rule 4, this sentence had its vel, and its outer parentheses, added by that rule.
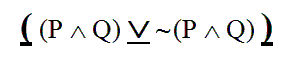
If this was the output of Rule 4, what must the two inputs have been? The two inputs would be everything here other than the vel and the outer parentheses. If we take away the vel and outer parentheses, what’s left will be just the two inputs that Rule 4 started with.
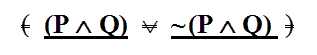
In tracing back from the output of Rule 4, to what its two inputs must have been, we’re basically just applying Rule 4 in reverse. Rule 4 takes two inputs, and adds a vel and a pair of parentheses to get its output. So to trace backwards, from output to the two original inputs, we just reverse Rule 4: take off outer parentheses, and take away a vel, and you’re left with the two inputs that Rule 4 started with.
Rule 4, in Reverse: remove the outermost pair of parentheses, and take a vel from between the two parts.
Applying Rule 4 in reverse to this sentence, we work our way backwards to the two original inputs.
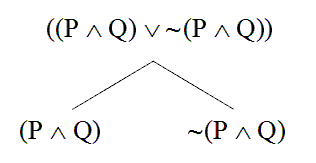
And now we apply this same rules-in-reverse strategy to trace each of these two sentences back to their parts.
Start with the left sentence, “(P
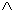Q)”. This sentence is clearly a disjunction, with a conjunction sign,
“
,”
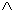as it main connective (indeed, its only connective). There’s only
one recursive rule that could have built this sentence: Rule 3 of our
grammar, the conjunction rule.
Here again, we can apply the rule in reverse to trace backward to its original inputs. Rule 3 puts a conjunction sign between the two parts, and adds parentheses. To work backward, we shift Rule 3 into reverse. Rule 3 in reverse takes away the outer parentheses, and removes a conjunction sign from between the two parts.
Rule 3, in Reverse: remove the outermost pair of parentheses, and take a conjunction sign from between the two parts.
Applying Rule 3 in reverse to “(P
Q),” we get this.
This sentence has now been traced back to its earliest ancestors, the sentence letters “P” and “Q”.
The other sentence, “~ (P
Q),” succumbs to the same backtracking strategy. “~ (P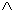
Q)” has a tilde at the extreme left, making this sentence a
negation. The only recursive rule that spits out negations is
Rule 2, the negation rule.
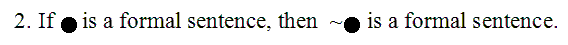
Rule 2 is very simple: it takes only one sentence as input, and adds a tilde to the left. Rule 2 in Reverse will then simply take a tilde off the left.
Rule 2, In Reverse: remove a tilde from the left of the sentence.
Applying Rule 2 in reverse, we work our way back to what must have been the original input of Rule 2 in this case.
This leaves only the sentence “(P
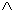Q),” which we’ve already encountered before. “(P Q)” is a conjunction, the handiwork of Rule 3. Unbuilding it with Rule 3 in reverse, we get this.
Rule 3, in Reverse: remove the outermost pair of parentheses, and take a conjunction sign from between the two parts.
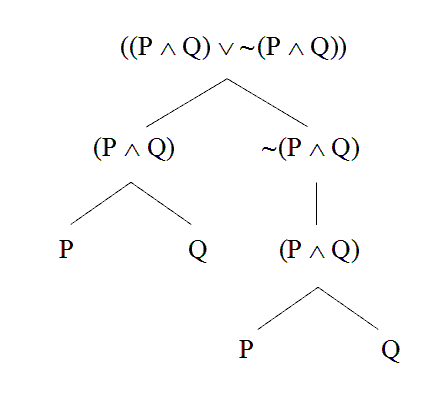
And now we’ve finished tracing the original sentence, “((P
Q) ~ (P
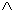Q)),” entirely back to sentences letters. That means we’ve
successfully reconstructed the grammatical tree for the original
sentence.
This illustrates a strategy that can be used for building a grammatical tree for a pre-existing formal sentence.
General strategy for building a grammatical tree for a pre-existing formal sentence:
“unbuild” the sentence, using the three recursive rules in reverse,
until only sentence letters remain at the bottom of the tree.
Rule 2, In Reverse: remove a tilde from the left of the sentence.
Rule 3, in Reverse: remove the outermost pair of parentheses, and take a conjunction sign from between the two parts.
Rule 4, in Reverse: remove the outermost pair of parentheses, and take a vel from between the two parts.
Rule 2, In Reverse: remove a tilde from the left of the sentence.
Rule 3, in Reverse: remove the outermost pair of parentheses, and take a conjunction sign from between the two parts.
Rule 4, in Reverse: remove the outermost pair of parentheses, and take a vel from between the two parts.
One final point: while I’ve illustrated here how we can always reconstruct the grammatical tree for any sentence, you might, quite fairly, ask why we would ever want to build a grammatical tree for a sentence. There are a couple of things that can be said in defense of building such a tree.
First, building the grammatical tree for a sentence supplies the ‘pedigree papers’ showing that the sentence in question is indeed a pure-bred formal sentence, built out of sentence letters by our recursive rules. If anyone challenges the grammatical credentials of our sentence, we can whip out a certificate of authenticity – the grammatical tree – to show that it really is a grammatical sentence – a “formal sentence”.
Second – and more importantly – grammatical trees illustrate what is a part of what in a formal sentence. The tree we just built, for example, clearly points out the two basic sub-parts of the original sentence.
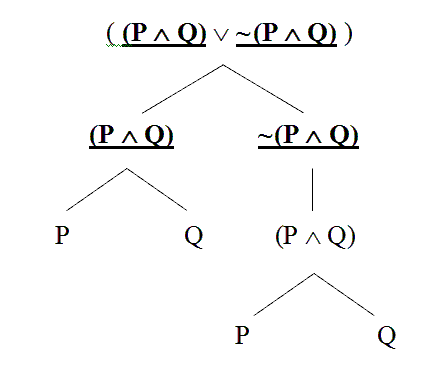
Likewise, it shows the two basic sub-parts of the conjunction, on the left.
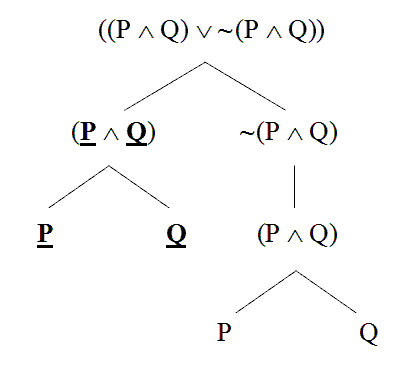
And it shows the one basic sub-part of the negation, on the right.
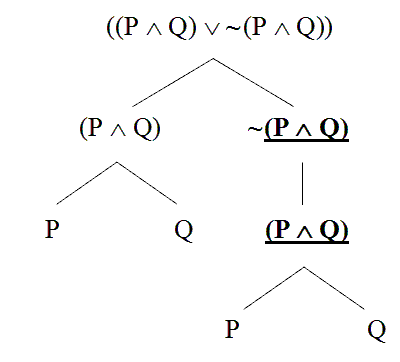
And so on. That information – what is a part of what is a part of what – will be a crucial ingredient in our formal test of validity. And since grammatical trees set out this information for us, grammatical trees will be an important tool when we test arguments for validity formally.
Finally, there’s one more good thing to be said about grammatical trees: we’re done talking about them!
Next stop: translation.