

(this is Chapter 20 of Adventures in Physics, available only online)
Ch 20, Wave Optics; 1 through 10
![]()
Homework for Ch 20, Wave Optics
1. We hear sound bend around building and through open doors; that is, we commonly notice the diffraction of sound waves far easier than the diffraction of light waves. Why is that?
Diffraction effects always depend upon the wavelength of the waves being diffracted or bent. The size of sound waves -- the wavelength of sound waves -- is far, far greater than the wavelength of light waves.
2. We even notice the diffraction of radio waves -- around trees and buildings -- far more readily than we ever see the diffraction of light waves. Both are EM waves. Why do we see diffraction of radio waves easier than diffraction of light waves?
The size of radio waves is still much greater than the size of light waves ("size" means "wavelength").
3. Consider two speakers set up as shown below. The same signal is applied to both speakers. If you walk in front of the speakers as shown in the sketch, you will notice areas where the volume is high and then areas where the volume is low. Explain why this happens.

As you walk along, in front of the two speakers, you will find the sound from the two speakers is "out of phase" and the two sound waves interfer destructively and the volume goes down. This destructive interference takes place where the distance from your ear to one speaker and the distance from your ear to the other speaker differ by an integer plus one-half times the wavelength of the sound. As you walk along to another place, you will find the sound from the two speakers is "in phase" and the two sound waves interfer constructively and the volume goes down. This constructive interference takes place where the distance from your ear to one speaker and the distance from your ear to the other speaker differ by an integer times the wavelength of the sound.
5. What is meant by constructive or destructive interference?
Constructive interference means the "signal" from two sources in "in phase" -- that is, both signals are trying "to do the same thing". This may mean two sound waves are trying to push air molecules in the same direction. Or two water waves may be trying to move the surface of the water in the same direction. Or two light waves may be trying to wiggle the electric field in the same direction. These two waves, then, reinforce each other and a large amplitude results.Destructive interference means the "signal" from two sources in "out of phase" -- that is, both signals are trying "to do opposite things". This may mean two sound waves are trying to push air molecules in opposite directions. Or two water waves may be trying to move the surface of the water in opposite directions -- one pushing the surface up while the other is pushing down. Or two light waves may be trying to wiggle the electric field in opposite directions. These two waves, then, tend to cancel each other and a small amplitude -- perhaps even zero -- results.
6. Consider light passing through a double slit as in Figure 20.5. What can you say about the paths of the light through the two slits that arrive at a bright maximum, a region of constructive interference? Again, consider light passing through a double slit as in Figure 20.5. What can you say about the paths of the light through the two slits that arrive at a dark minimum, a region of destructive interference?
Light waves that pass through the two slits and arrive at a bright maximum have traveled along two paths that are the same length for the central maximum and, for other maxima, they have traveled two distances that differ by an integral number of wavelengths. This means the two light waves are "in phase" and that they constructively interfere or add together constructively.Light waves that pass through the two slits and arrive at a dark minimum have traveled along two paths or two distances that differ by 1/2, 3/2, 5/3, 7/2, ... (an integer plus one-half) wavelengths. This means the two light waves are "out of phase" and that they destructively interfere or add together destructively.
7. Again, consider light passing through a double slit as in Figure 20.5. If the slit separation distance d is made greater, how will that affect the interference pattern?
As the slit separation distance d is made greater, the whole interference pattern is squeezed closer together.
8. How will the two interference patterns compare and differ if you first illuminate a double slit with red laser light and then illuminate the same double slit with blue laser light?
All interference or diffraction patterns depend upon the wavelength of the light (or whatever wave) involved. Red light has the longest wavelength (about 700 nm) while blue light has short wavelength (about 400 nm). To get "out of phase" and then back "in phase", we will need to go through a greater angle with the red light than with the blue light.
9. What is meant by coherent light? Why must the light falling on the double slit be coherent in order to see the interference pattern?
Coherent light is light that has a definite and constant phase relation. Coherent light is like a marching band that is in step with the drummer. If two rays of coherent light interfere constructively at one time they will always interfer constructively.Light may also be incoherent. Light from a lightbulb comes from many different atoms giving out a photon -- a piece of light -- independently of each other. While light from two different parts or areas of a light bulb might interfer constructively at one moment, a moment later the light from those same two different parts or areas of a light bulb might interfere destructively -- or somewhere in between -- because the photons -- or pieces of light -- will have a different phase.
10. What difference do you expect if you look at a white light source first through a diffraction grating with 5 000 lines per centimeter and then through a diffraction grating with 10 000 lines per centimeter?
The line separation distance is only one-half as great for the 10 000 lines/cm grating. This is very similar to the double slit interference pattern when the two slits are separated only half as far. Moving the lines closer together spreads the interference pattern out, making a greater separation between the maxima.
11. When light passes through a diffraction grating, maxima or bright areas of constructive interference appear just as with double slit diffraction. These bright areas appear when the difference in path length for light from adjacent slits is an integer times the wavelength of the light. However, the diffraction pattern from a diffraction grating goes very rapidly from bright to dark--the bright areas become sharp lines or dots--but the diffraction pattern from a double slit goes very gradually from bright to dark. What causes this difference? The difference is sketched below.
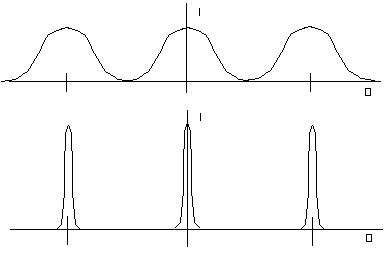
The maxima -- the areas of constructive interference -- occur at the same places for the same reasons. Maxima -- or constructive interference -- occurs when the light from adjacent slits travels a distance equal to 1, 2, 3, 4, 5, . . . wavelengths -- an integer times the wavelength. If the difference in distance for adjacent slits is an integer times a wavelength then the difference in distance for all slits must also be an integer times a wavelength. A diffraction grating has many slits. Suppose the difference in distance for two adjacent slits is, say one-tenth of a wavelength. Then the difference in distance for one slit and another slit, five slits away would be five-tenths of a wavelength. That's one-half a wavelength and that means the light from these two slits would then produce destructive interference. With so many slits, if they are not all "in phase" for constructive interference, one slit will surely destructively interfer with another one somewhere else.
12. When white light is passed through a diffraction grating, a colored spectrum is produced. Explain why and tell which color of the spectrum is nearest the white central maximum.
Bright light occurs for constructive interference. That means the difference in path length is one (or two or three or some integer number of) wavelength(s). Violet and blue will be seen closer to the central maximum -- then green and yellow and orange and finally red, farthest from the white central maximum.
![]()
Typical multiple-guess questions over this material:
1. According to Huygens' principle, every point on a wave
a) is a diffraction source.b) behaves as a source of new waves.
c) is the superposition of every other part of the wave.
d) all of the above.
2. Consider plane waves incident upon a barrier with a small opening. After passing through the opening, the waves
a) continue as plane wavesb) spread out
c) are polarized
d) converge
3. Light from a laser is
a) monochromaticb) in phase
c) coherent
d) all of the above
4. In the interference pattern produced by shining a laser through two slits (Young's double slit experiment), the bright areas are the result of
a) destructive interference.b) polarization.
c) constructive interference.
d) restructive construction.
5. When light passes through a diffraction grating it is bent. Light with a greater wavelength will be bent
a) through a smaller angle.b) the same (bending is independent of wavelength).
c) through a larger angle.
6. When you view a white light source through a diffraction grating you will see brightly colored spectra with
a) red on the inside and violet on the outsideb) violet on the inside and red on the outside
c) yellow on the inside and green on the outside
d) yellow on the outside and green on the inside
7. Diffraction effects depend upon wavelength. You can see more details in a photograph taken through a microscope using
a) infra-red (IR) radiationb) visible red light
c) visible blue light
d) ultra-violet (UV) radiation
8. Diffraction effects depend upon wavelength. Computer chips are manufactured using photographic processes. To make smaller, finer, higher resolution circuits on a computer chip, manufacturers use
a) infra-red (IR) radiationb) visible red light
c) visible blue light
d) ultra-violet (UV) radiation
9. In regions where the soap film on a soap bubble is very, very thin, you would expect to see
a) a bright, white areab) a reddish area
c) a blueish (or violet) area
d) a dark area
10. If red light and blue light are passed through a small slit, you will find the light spread out with a broad central maximum or bright area followed by a dark minimum on either side. The width of this central maximum will be
a) the same for both colors.b) greater for red light
c) greater for blue light
Answers to typical multiple-guess questions over this material:
1. According to Huygens' principle, every point on a wave
a) is a diffraction source.b) behaves as a source of new waves.
c) is the superposition of every other part of the wave.
d) all of the above.
2. Consider plane waves incident upon a barrier with a small opening. After passing through the opening, the waves
a) continue as plane wavesb) spread out
c) are polarized
d) converge
3. Light from a laser is
a) monochromaticb) in phase
c) coherent
d) all of the above
4. In the interference pattern produced by shining a laser through two slits (Young's double slit experiment), the bright areas are the result of
a) destructive interference.b) polarization.
c) constructive interference.
d) restructive construction.
5. When light passes through a diffraction grating it is bent. Light with a greater wavelength will be bent
a) through a smaller angle.b) the same (bending is independent of wavelength).
c) through a larger angle.
6. When you view a white light source through a diffraction grating you will see brightly colored spectra with
a) red on the inside and violet on the outsideb) violet on the inside and red on the outside
Red light has a l-o-n-g-e-r wavelength so it will be bent more.c) yellow on the inside and green on the outside
d) yellow on the outside and green on the inside
7. Diffraction effects depend upon wavelength. You can see more details in a photograph taken through a microscope using
a) infra-red (IR) radiationb) visible red light
c) visible blue light
d) ultra-violet (UV) radiation
8. Diffraction effects depend upon wavelength. Computer chips are manufactured using photographic processes. To make smaller, finer, higher resolution circuits on a computer chip, manufacturers use
a) infra-red (IR) radiationb) visible red light
c) visible blue light
d) ultra-violet (UV) radiation
9. In regions where the soap film on a soap bubble is very, very thin, you would expect to see
a) a bright, white areab) a reddish area
c) a blueish (or violet) area
d) a dark area
10. If red light and blue light are passed through a small slit, you will find the light spread out with a broad central maximum or bright area followed by a dark minimum on either side. The width of this central maximum will be
a) the same for both colors.b) greater for red light
because red light has a longer wavelengthc) greater for blue light
| Back to 3050's Home Page | Back to Calendar | ToC, Ch 20 |
![]()
(C) 2003, Doug Davis; all rights reserved