Excursions in Physics

Homework, Chapter 10: Periodic Motion

(this is Chapter 10 of Adventures in Physics, available only online)

Ch 10, Periodic Motion; 3, 4, 5, 9, 13, 14, 15, 16

3. Describe some kind of periodic motion that is not simple harmonic motion.

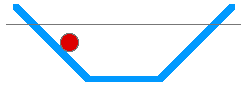
A ball rolling down an inclined plane, across a horizontal surface, and up another inclined plane -- as shown above -- is an example of periodic motion that is not simple harmonic motion. The ball experiences a constant force as it rolls down the inclined plane. It experiences no force as it moves along the horizontal plane. And it experiences another constant forceas it rolls up the other inclined plane. The forces are quite different from the forces of a spring. But the motion does repeat itself so it is periodic.

4. Explain why increasing the mass in a spring-and-mass simple harmonic oscillator causes the period to increase.

Think of what Newton's Second Law, F = m a, can tell us about a spring-and-mass system. If the mass increases, and everything else remains the same, Newton's Second Law tells us the acceleration must decrease. The mass will move more slowly. If it moves more slowly, it will require more time to go through one period so the period will increase.

5. Explain why increasing the stiffness of the spring in a spring-and-mass simple harmonic oscillator causes the period to decrease.

Again, think of what Newton's Second Law, F = m a, can tell us about a spring-and-mass system. If the spring constant (or the stiffness or strength of the spring) increases, and everything else remains the same, Newton's Second Law tells us the acceleration must increase. Increasing the spring constant k means the spring exerts a greater force. This greater force -- acting on the same mass -- causes a greater acceleration. The mass will move more rapidly. If it moves more rapidly, it will require less time to go through one period so the period will decrease.

9. If a carefully calibrated pendulum were over a large oil deposit, where the acceleration due to gravity is slightly decreased, what would happen to the pendulum's period?

From laboratory experiments and from the text we know that the period of a simple pendulum is given by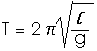
The density of oil is far less than the average density of the Earth. Being over a very large oil deposit means the acceleration of gravity there would be slightly less than the "normal" value. A smaller value of g means the period of a simple pendulum would be greater. Actual, working, petroleum geologists do use this technique (and many others) in looking for oil deposits.

Likewise, the density of iron ore is somewhat greater than the average density of the Earth. So being over a very large deposit of iron ore means there is more mass nearby and the acceleration of gravity there will be slightly greater than the "normal" value. A larger value of g means the period of a simple pendulum there will be less.

13. As the amplitude of a damped oscillator decays, there is less energy stored in the oscillator. What has happened to the energy it started with?

Something else has taken the energy -- probably in the form of heat. Typically the air surrounding it has been heated somewhat. If we really are doing this underwater, then the water has been made warmer. If our oscillator moves a mass back and forth across a horizontal surface, the bottom of the mass and the horizontal surface exert friction forces on each other and heat is generated there. Energy is never really lost but large-scale mechanical energy can be turned into heat.

14. Can the speed of a simple harmonic oscillator be zero? Where?

At each extreme of its motion -- when its distance from equilibrium is equal to the amplitude -- a simple harmonic oscillator momentarily comes to a stop. If it is stopped, it has no Kinetic Energy. At those points, all of its energy is stored in Potential Energy.

15. Can the acceleration of a simple harmonic oscillator be zero? Where?

The acceleration is zero whenever, or wherever, the force is zero. The force is zero at the equilibrium position.

16. If your shock absorbers are carefully adjusted to give a very good and comfortable ride with just the driver in the car, how will the ride be affected if your car is fully loaded with passengers and luggage?

With your car fully loaded with passengers and luggage, the mass of the car is greater. The shock absorbers will not exert enough force to keep the car from oscillating. With the car fully loaded, you will notice more bounce each time you go over a pot hole or an expansion joint.

Typical Multiple Choice Questions:

1. Increasing the amplitude of a simple pendulum makes its period

A) longer
B) shorter

C) unchanged

2. Increasing the mass of a simple pendulum makes its period

A) longer
B) shorter

C) unchanged

3. Increasing the length of a simple pendulum makes its period

A) longer
B) shorter

C) unchanged

4. Increasing the amplitude of a mass-and-spring simple harmonic oscillator makes its period

A) longer
B) shorter

C) unchanged

5. Increasing the mass of a mass-and-spring simple harmonic oscillator makes its period

A) longer
B) shorter

C) unchanged

6. A mass-and-spring simple harmonic oscillator has maximum kinetic energy

A) at its equilibrium position
B) when its displacement equals its amplitude

C) half way between equilibrium and amplitude

D) two-thirds of the way between equilibrium and amplitude

7. A mass-and spring simple harmonic oscillator has maximum potential energy at

A) at its equilibrium position
B) when its displacement equals its amplitude

C) half way between equilibrium and amplitude

D) two-thirds of the way between equilibrium and amplitude

8. The amplitude of a simple harmonic oscillator is

A) the time required for one oscillation
B) the number of oscillators per second

C) the energy stored in the oscillations

D) the maximum distance moved from equilibrium

9. The period of a simple pendulum depends upon its

A) mass
B) amplitude

C) length

D) all of the above

10. The period of a certain simple harmonic oscillator is 0.1 s; its frequency is

A) 0.1 Hz
B) 1.0 Hz

C) 10.0 Hz

D) 100 Hz

11. Ordinary household electricity is alternating current with a frequency of 60 Hz. Its period is

A) 60 cycles per second
B) 120 cycles per second

C) 0.0167 s

D) 0.0333 s

12. If you apply a force to an oscillator at its natural frequency, you will produce motion

A) at exactly twice that frequency
B) at exactly one-half that frequency

C) with large amplitude

D) with an amplitude that dies out or gets smaller.

13. There are "signals" of many different frequencies coming into the antenna of your radio. Only the one with a particular frequency is amplified and produces the sound you listen to. This is an example of

A) damping
B) amplitude degeneration

C) timbre or quality

D) resonance

14. If a carefully calibrated pendulum were over a very large oil deposit, where the acceleration due to gravity is slightly decreased, what would happen to the pendulum's period?

A) increase
B) stay the same

C) decrease

15. Where is the speed of a simple harmonic oscillator zero?

A) at its equilibrium position
B) when its displacement equals its amplitude

C) half way between equilibrium and amplitude

D) two-thirds of the way between equilibrium and amplitude

Answers to these Typical Multiple Choice Questions:

1. Increasing the amplitude of a simple pendulum makes its period

A) longer
B) shorter

C) unchanged

2. Increasing the mass of a simple pendulum makes its period

A) longer
B) shorter

C) unchanged

3. Increasing the length of a simple pendulum makes its period

A) longer
B) shorter

C) unchanged

4. Increasing the amplitude of a mass-and-spring simple harmonic oscillator makes its period

A) longer
B) shorter

C) unchanged

5. Increasing the mass of a mass-and-spring simple harmonic oscillator makes its period

A) longer
B) shorter

C) unchanged

6. A mass-and-spring simple harmonic oscillator has maximum kinetic energy

A) at its equilibrium position
B) when its displacement equals its amplitude

C) half way between equilibrium and amplitude

D) two-thirds of the way between equilibrium and amplitude

7. A mass-and spring simple harmonic oscillator has maximum potential energy at

A) at its equilibrium position
B) when its displacement equals its amplitude

C) half way between equilibrium and amplitude

D) two-thirds of the way between equilibrium and amplitude

8. The amplitude of a simple harmonic oscillator is

A) the time required for one oscillation
B) the number of oscillators per second

C) the energy stored in the oscillations

D) the maximum distance moved from equilibrium

9. The period of a simple pendulum depends upon its

A) mass
B) amplitude

C) length

D) all of the above

10. The period of a certain simple harmonic oscillator is 0.1 s; its frequency is

A) 0.1 Hz
B) 1.0 Hz

C) 10.0 Hz; f = 1/T, f = 1/(0.1 s) = 10/s = 10 cyc/s = 10 Hz

D) 100 Hz

11. Ordinary household electricity is alternating current with a frequency of 60 Hz. Its period is

A) 60 cycles per second
B) 120 cycles per second

C) 0.0167 s; T = 1/f = 1/(60 Hz) = 1/(60 cyc/s) = (1/60) s = 0.0167 s

D) 0.0333 s

12. If you apply a force to an oscillator at its natural frequency, you will produce motion

A) at exactly twice that frequency
B) at exactly one-half that frequency

C) with large amplitude

D) with an amplitude that dies out or gets smaller.

A) damping
B) amplitude degeneration

C) timbre or quality

D) resonance

14. If a carefully calibrated pendulum were over a very large oil deposit, where the acceleration due to gravity is slightly decreased, what would happen to the pendulum's period?

A) increase;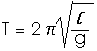
B) stay the same

C) decrease

15. Where is the speed of a simple harmonic oscillator zero?

A) at its equilibrium position
B) when its displacement equals its amplitude

C) half way between equilibrium and amplitude

D) two-thirds of the way between equilibrium and amplitude