PHY 3050C
Excursions in Physics
“Excursions Online”
Mid-Term Exam
May 18, 1999

| Return to Calendar |

v = x / t	v = vi + a t
a = v / t	x = xi + vi t + (1/2) a t2
v = r
F = m a
F12 = - F21
w = m g	g = 9.8 m/s2 10 m/s2
Impulse = F t
Impulse = p
Ptot,i = Ptot,f	KE = (1/2) m v2
W = F s cos	Etot = KE + PE
P = W / t	PEg = m g h
	Fs = - k x
Fg = G Mm/r2	PEs = (1/2) k x2
Fc = m v2 / r	Xcm = mi xi / mi
Angular Momentum = I	Ycm = mi yi / mi

For every question, also consider the following as a possible answer:
E) none of the above

A) by Aristotle in ancient Greece
B) by Ptolemy in Egypt
C) by Galileo in Italy
D) by Joule in England

2. To measure the time needed to investigate motion,

A) Aristotle used the pendulum clock which had just been invented
B) Ptolemy used a sundial
C) Galileo invented his own water clocks
D) Newton invented the pendulum clock

 
3. What is the average speed of a motorcycle that travels 60 m in 3 s?

A) 40 m/s
B) 20 m/s

v = dist / time

v = 60 m / 3 s

v = 20 m/s

C) 10 m/s
D) 9.8 m/s

 
4. What is the average speed of a car that travels 75 km in 5 h?

A) 135 km/h
B) 15 km/h

v = dist / time

v = 75 km / 5 h

v = 15 km/h

C) 10 km/h
D) 9.8 km/h

 
5. Consider a train that has an acceleration of 2 m/s². Initially, at time t = 0, it has a velocity of v_i = 10 m/s. What is its speed at t = 3 s?

A) 20 m/s
B) 16 m/s

v = v_i + a t

v = 10 m/s + ( 2 m/s² )( 3 s)

v = 10 m/s + 6 m/s

v = 16 m/s

C) 12 m/s
D) 6 m/s

 
6. Consider a car that starts at rest and accelerates at 4 m/s² for 3 seconds. At that time, t = 3 s, how fast is it going?

A) 36 m/s
B) 24 m/s
C) 12 m/s

v = v_i + a t

v = 0 + ( 4 m/s² )( 3 s)

v = 12 m/s

D) 9 m/s

 
7. Consider a car that starts at rest and accelerates at 3 m/s² for 4 seconds. At that time, t = 4 s, how far has it gone?

A) 36 m
B) 24 m

x = x_i + v_i t + (¹/₂) a t ²

x = 0 + 0 + (¹/₂) ( 3 m/s ² ) ( 4 s ) ²

x = (¹/₂) ( 3 m/s ² ) ( 16 s ² )

x = 24 m

C) 12 m
D) 9 m

8. Consider a ball that is thrown upward at the edge of a canyon with an initial velocity of 20  m/s. Three seconds later, at t = 3 s, what is its velocity?

A) 30 m/s
B) 15 m/s
C) - 10 m/s

v = v_i + a t

v = 20 m/s + ( - 10 m/s ² ) ( 3 s )

v = 20 m/s - 30 m/s

v = - 10 m/s 

D) - 30 m/s

9. Consider a ball that is thrown straight upward at the edge of a canyon with an initial velocity of 20 m/s. Three seconds later, where is it located? Take its initial position, at the edge of the canyon, to be the origin; that is, y_i = 0.

A) 30 m
B) 15 m

x = x_i + v_i t + (¹/₂) a t ²

y = y_i + v_yi t + (¹/₂) a_y t ²

y = 0 + (20 m/s)(3 s) + (¹/₂)( - 10 m/s ²)(3 s) ²

y = 60 m - 45 m

y = 15 m

C) - 10 m
D) - 30 m
 

10. Consider a ball that is thrown horizontally from the edge of a building with an initial velocity of 10 m/s. The building is 5 m above the driveway below. How far from the building does the ball strike the driveway?

A) 5 m
B) 10 m

How long does it take to fall 5 m?

x = x_i + v_i t + (¹/₂) a t ²

y = y_i + v_yi t + (¹/₂) a_y t ²

- 5 m = 0 + 0 + (¹/₂) ( - 10 m/s ² ) t ²

- 5 m = ( - 5 m/s ²) t ²

1 s ² = t ²

t = 1 s

Now we can ask how far does it travel horizontally in this time,

x = x_i + v t

Remember, a_x = 0,

x = 0 + (10 m/s)(1 s)

x = 10 m/s

C) 15 m
D) 20 m

 

11. When a ball or stone or other object is thrown or hit or fired, and air resistance can be neglected, the resulting motion is known as projectile motion The path of an object in projectile motion is

A) a straight line
B) a hyperbola
C) a parabola
D) a quadrant of a circle
 

12. Projectile motion is a combination of

A) horizontal motion with constant, non-zero acceleration and vertical motion with constant velocity
B) horizontal motion with constant non-zero acceleration and vertical motion with constant, non-zero acceleration
C) horizontal motion with constant velocity and vertical motion with constant, non-zero acceleration
D) horizontal motion with constant velocity and vertical motion with constant velocity
 

13. Consider a ball thrown from a level surface with an initial upward velocity of 20 m/s and an initial horizontal velocity of 5 m/s. How long is the ball in the air?

A) 1.0 s
B) 2.0 s
C) 4.0 s

When the ball returns to the level surface, its vertical speed will be the same, 20 m/s.

Or, when the ball returns to the level surface, its vertical velocity will be - 20 m/s

v_y = v_yi + a_y t

- 20 m/s = 20 m/s + ( - 10 m/s² ) t

- 40 m/s = ( - 10 m/s² ) t

4 s = t

D) 5.0 s

14. Consider a ball thrown from a level surface with an initial upward velocity of 20 m/s and an initial horizontal velocity of 5 m/s. Where does it land? That is, measured from its initial position, where does it come back to and strike the level surface?

A) 10 m
B) 15 m
C) 20 m

In the previous problem, we found that the ball was in the air for 4 seconds. How far does it travel horizontally during that time?

x = x_i + v_x t

Remember, a_x = 0

x = 0 + (5 m/s)(4 s)

x = 20 m

D) 30 m

15. “Kinematics” is a description of motion. “Dynamics”is

A) an alternate description of motion in terms of Earth, air, fire, and water.
B) an explanation of the cause and effect of motion.
C) another name for the dynamic use of the Conservation of Energy.
D) the Conservation of Momentum.

 
16. Newton's First Law of Motion states that, in the absence of a net force, an object in motion will

A) eventually come to rest.
B) continue in motion but slow down until it stops.
C) continue in motion with the same speed along the same straight line.
D) continue along the same straight line with a decrease in speed

 
17. Mass is a measure of

A) the volume of an object
B) the size of an object multiplied by its speed
C) the velocity of an object multiplied by its mass
D) how difficult it is to change the motion of an object

18. The weight of an object is

A) another name for the mass of an object
B) the sum of all the forces on an object (the net force)
C) the force of gravity on an object
D) always less than the mass, even in a vacuum

19. The net force on a 10-kg object, at rest, is

A) 98 N
B) 49 N
C) 10.0 N
D) zero

The net force on any object at rest is zero.

 
20. The net force on a 10-kg object, in free fallt, is

A) 98 N

w = m g

w = (10 kg) (9.8 m/s ²)

B) 49 N
C) 10.0 N
D) zero

21. Harry the Painter has a weight of 500 N. When he is suspended as shown in the sketch here, what is the tension in the rope?

A) 1000 N
B) 500 N

The rope exerts a force on Harry only once. That single force must support his weight.

C) 250 N
D) 25 N

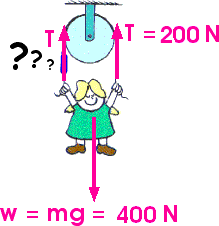
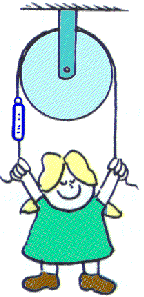
22. Little Nellie Newton has a mass of 40 kg. What is the tension in the cord as Nellie suspends herself as shown above?

A) 800 N
B) 400 N
C) 200 N

w = m g

w = (40 kg) (10 m/s ²)

w = 400 N

That weight is supported by the cord in her left hand AND by the cord in her right hand. The tension in the cord is one-half her weight or 200 N.

D) 100 N

23. A force of 24 N acts on an object whose mass is 8 kg. This causes the object to accelerate at

A) 2 m/s²
B) 3 m/s²

F = m a

24 N = ( 8 kg ) a

24 N = ( 8 kg ) ( 3 m/s ² )

a = 3 m/s ²

C) 8 m/s²
D) 10 m/s²

 
24. A car, with mass of 1,200 kg, accelerates at 2 m/s². The net force exerted on the car must be

A) 300 N
B) 600 N
C) 900 N
D) 1,200 N

E) None of the above

F = m a

F = ( 1,200 kg) ( 2 m/s ² )

F = 2,400 kg m / s ²

F = 2,400 N

 
25. The weight of a 1,000-kg car is

A) 500 N
B) 1,000 N
C) 2,000 N
D) 10,000 N

w = m g

w = ( 1,000 kg ) ( 10 m/s ² )

w = 10,000 N

26. A fireman, whose weight is 500 N, slides down a pole with an acceleration of 3 m/s². The forces that act on him are his weight pulling him down and the force of friction pulling up on him to slow him down. The force of friction must be

A) 90 N
B) 150 N
C) 350 N

w = m g

500 N = m ( 10 m/s ² )

500 N = ( 50 kg ) ( 10 m/s ² )

m = 50 kg

If the fireman has an acceleration of 3 m/s ², the the net force is

F_net = m a

F_net = ( 50 kg ) ( 3 m/s ² ) = 150 N

This net force is the sum of the weight ( 500 N ) pulling down and the friction force F_friction pulling up,

F_net = w - F_friction

150 N = 500 N - F_friction

150 N = 500 N - 350 N

F_friction = 350 N

D) 500 N

 

27. Suppose you are driving along in an open car and throw a ball straight up into the air. While the ball is still in the air you step on the brakes. Where does the ball land relative to the car?

A) behind the car
B) back into the car
C) in front of the car

28. Newton used the term “motion” to mean what we now call “momentum”. “Momentum” is

A) mass times acceleration
B) force times distance
C) mass times velocity

p = m v

D) weight multiplied by time

29. Impulse is

A) always conserved.
B) conserved only in “elastic collisions”.
C) conserved in “inelastic collisions”.
D) equal to the change in momentum.

30. Impulse is

A) force multiplied by distance.
B) force divided by distance.
C) force multiplied by time.
D) force divided by time.

31. Which of the following has the largest momentum relative to Earth?

A) a tightrope walker crossing Niagara Falls.
B) a pickup truck speeding along a highway.
C) a Mack truck sitting in the parking lot. [ p = 0 since v = 0].
D) the Science building on campus. [ p = 0 since v = 0].

32. A moving object on which no forces are acting will continue to move with constant

A) acceleration
B) impulse
C) momentum

F = 0 means a = 0 and v = constant or p = constant

D) all of these

33. Conservation of momentum is directly related to

A) Newton's First Law of Motion
B) Newton's Second Law of Motion
C) Newton's Third Law of Motion

From F₁₂ = - F₂₁, we found p₁₂ = - p₂₁

and that led to P_Tot,i = P_Tot,f or P_Tot = constant.

D) International shortages of momentum

34. A rifle recoils from firing a bullet. The speed of the rifle's recoil is small because the

A) force against the rifle is smaller than against the bullet.

[ The forces are the same by Newton's Third Law ].

B) momentum of the rifle is smaller than that of the bullet.

[ The momenta are the same -- but in opposite directions -- by Conservation of Momentum ] .

C) rifle has more kinetic energy than the bullet.

[ The bullet has more KE than the rifle ] .

D) momentum of the rifle is larger than that of the bullet.

[ The momenta are the same -- but in opposite directions -- by Conservation of Momentum ] .

E) None of the above!

35. Two objects, A and B, have the same size and shape, but A is twice as heavy as B. When they are dropped simultaneously from a tower, they reach the ground at the same time, but A has a greater

A) speed [ They have the same speed ] .
B) acceleration [ They have the same acceleration ] .
C) momentum

p = m v

They have the same velocity.

Therefore the one with twice the mass has twice the momentum

D) all of the above

36. A car traveling along the highway needs a certain amount of force exerted on it to stop. Greater stopping force will be required when the car has

A) more mass.
B) more momentum.
C) less stopping distance.
D) all of the above

 
37. A 5 kg ball has a momentum of 15 kg m/s. What is the ball's speed?

A) 3 m/s

p = m v

15 kg m/s = ( 5 kg ) v

15 kg m/s = ( 5 kg ) ( 3 m/s )

v = 3 m/s

B) 5 m/s
C) 45 m/s
D) 75 m/s

38. A ball is moving at 3 m/s and has a momentum of 45 kg m/s. What is the ball's mass?

A) 3 kg
B) 5 kg
C) 15 kg

p = m v

45 kg m/s = m ( 3 m/s)

45 kg m/s = ( 15 kg ) ( 3 m/s )

m = 15 kg

D) 135 kg

39. If you push an object twice as far while applying the same force you do

A) half as much work.
B) the same amount of work.
C) twice as much work.
D) four times as much work.

40. If you push an object just as far while applying twice the force you do

A) half as much work.
B) the same amount of work.
C) twice as much work.
D) four times as much work.

41. Exert 2 N for a distance of 2 m in 2 s and you deliver a power of

A) 1.0 W
B) 2.0 W

P = W/t

W = F s

W = ( 2 N ) ( 2 m ) = 4 N m = 4 J

P = 4 J / 2 s

P = 2 J/s = 2 W

C) 4.0 W
D) 8.0 W

42. Exert 100 J of work in 50 s and your power output is

A) 0.5 W
B) 1.0 W
C) 2.0 W

P = W/t

P = 100 J / 50 s

P = 2 J/s = 2 W

D) 4.0 W

43. An object is raised above the ground gaining a certain amount of potential energy. If the same object is raised twice as high it gains

A) half as much energy
B) the same amount of energy
C) twice as much energy

PE_g = m g h

PE_g = m g h

D) four times as much energy

 
44. An object that has kinetic energy must be

A) elevated
B) falling
C) moving

KE = (1/2) m v ²

D) at rest

45. An object that has potential energy may have this energy because of its

A) speed
B) acceleration
C) momentum
D) position

46. A clerk can lift containers a vertical distance of 1 meter or can roll them up a 2 meter-long ramp to the same elevation. With the ramp, the applied force required is about

A) one-fourth as much
B) half as much

W = F s

F s = F s

C) the same

D) twice as much

 
47. When a car is braked to a stop, its kinetic energy is transformed to

A) energy of motion
B) heat energy
C) stopping energy
D) potential energy

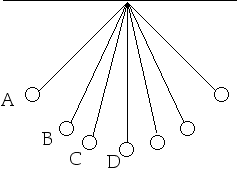
48. For which position above does the ball on the end of the string have the greatest gravitational potential energy?

A) PE_g = m g h and position A has the greatest height h.

49. For which position above does the ball on the end of the string have the greatest kinetic energy?

D) Position D has the lowest height h so it has the smallest gravitational potential energy PE_g.

Total Energy remains constant, E = const .

Total Energy is the sum kinetic energy and potential energy, E = KE + PE_g .

When (or where) PE_g is minimum is when (or where) KE is maximum.

 
50. Which requires more work: lifting a 5 kg sack vertically 2 meters or lifting a 10 kg sack vertically 4 meters?

A) lifting the 5 kg sack
B) both require the same amount of work
C) lifting the 10 kg sack
D) both require the same amount of force

51. A 10 kg sack is lifted 2 meters in the same time as a 5 kg sack is lifted 4 meters. The power expended in raising the 10 kg sack compared to the power used to lift the 5 kg sack is

A) half as much
B) the same
C) twice as much
D) four times as much

52. A 3 kg mass is held 5 m above the ground. What is the approximate potential energy of the mass with respect to the ground?

A) 25 J
B) 75 J
C) 150 J

PE_g = m g h

PE_g = (3 kg)(10 m/s ²)(5m)

PE_g = 150 J

D) 300 J

53. A 5 kg mass has 50 J of potential energy with respect to the ground. Approximately how far is it located above the ground?

A) 0.5 m
B) 1 m

PE_g = m g h

50 J = ( 5 kg ) ( 10 m/s ² ) h

50 J = ( 5 kg ) ( 10 m/s ² ) ( 1 m )

h = 1 m

C) 5 m
D) 10 m

 
54. Using 2,000 J of work, a model elevator is raised from the ground floor to the second floor in 10 seconds. How much power does the elevator use?

A) 20 W
B) 200 W
C) 2 kW
D) 20 kW

 
55. A car moves 3 times as fast as another identical car. Compared to the slower car, the faster car has

A) the same kinetic energy
B) 3 times the kinetic energy
C) 9 times the kinetic energy

KE = (1/2) m v ²

3 ² = 9

D) 27 times the kinetic energy

56. A car moving at 40 km/hr skids 20 m with locked brakes. How far will the car skid with locked brakes if it is traveling at 120 km/hr?

A) 60 m
B) 90 m
C) 120 m
D) 180 m

120 km/hr = 3 x (40 km/hr)

The speed has been increased three times.

That means the Kinetic Energy has been increased nine times.

Nine times as much work is required to stop the car.

The force is the same -- since the brakes are locked and the car is skidding.

The skid marks will be nine times as long, 180 m.

57. When a rifle is fired it recoils so both the bullet and rifle are set in motion. The rifle and bullet ideally acquire equal but opposite amounts of

A) kinetic energy
B) momentum

Momentum is always conserved.

C) potential energy
D) all of the above

58. What does an object have when moving that it doesn`t have when at rest?

A) momentum

p = m v

B) energy
C) mass
D) all of the above

59. If an object has kinetic energy, then it also must have

A) momentum
B) velocity
C) speed
D) all of the above

60. According to Kepler's laws, the paths of planets about the Sun are

A) straight lines
B) parabolas
C) ellipses
D) hyperbolas

 

61. According to Newton, the greater the masses of interacting objects, the

A) greater the force of gravity, by the product of the masses

F = G M m / r ²

B) less the force of gravity
C) greater the force of gravity, by the square of the masses
D) less the force of gravity, inversely as the square of the masses

62. According to Newton, the greater the distance between masses of interacting objects, the

A) greater the force of gravity, proportional to the distance
B) less the force of gravity, inversely as the distance
C) greater the force of gravity, proportional to the square of the distance
D) less the force of gravity, inversely as the square of the distance

F = G M m / r ²

 
63. What is the force of gravity on a 500-newton woman standing on Earth's surface?

A) 9.8 N
B) 50 N
C) 500 N

Units of newtons are units of force so 500 N already is the force of gravity.

D) 5,000 N

 
64. If the mass of Earth somehow increased with no change in radius, your weight would

A) increase

F = G M m / r ²

F = G M m / r ²

B) decrease
C) stay the same

 
65. If the radius of Earth somehow decreased with no change in mass, your weight would

A) increase
B) decrease

F = G M m / r ²

F = G M m / r ²

C) stay the same

 
66. If Earth's mass decreased to one-third its original mass with no change in radius, then your weight would

A) decrease to one-ninth its original value
B) decrease to one-third its original value

F = G M m / r ²

C) remain the same
D) increase to three times its original value

 
67. The force of gravity acting on the Space Shuttle in orbit is nearly

A) zero
B) equal to the weight of the Space Shuttle at Earth's surface

F = G M m / r ²

The distance r from the center of Earth to the Space Shuttle is nearly the same in orbit as at Earth's surface.

C) about one-tenth its weight at Earth's surface
D) about one-one hundredth its weight at Earth's surface

68. A woman who normally weighs 500 N stands on top of a very tall ladder so she is one earth radius above the earth's surface. How much would she weigh there?

A) zero
B) 125 N

F = G M m / r ²

If the distance r is doubled then the weight (or the force of gravity) is one-fourth as much.

C) 250 N
D) 500 N

69. The force of gravity acts on all apples on an apple tree. Some apples are twice as far from the ground as others. These twice- as-high apples, for the same mass, have practically

A) one-fourth the weight
B) one-half the weight
C) the same weight

F = G M m / r ²

The distance r from the center of Earth to an apples is indistinguishable for all apples an an apple tree.

D) twice the weight

70. The planet Jupiter is about 300 times as massive as Earth, yet on its surface you would weigh only about 3 times as much. This is because

A) your mass is 100 times less on Jupiter.
B) Jupiter is significantly farther from the sun.
C) Jupiter's radius is 10 times Earth's radius.
D) you are 100 times more weightless there.

71. Horses that move with the fastest linear speed on a merry-go-round are

A) located nearer to the center
B) located nearer to the edge
C) always white : - )
D) in front of the slower ones :-)

72. An industrial flywheel has a greater rotational inertia when most of its mass is

A) nearer the axis
B) nearer the rim
C) spread out evenly

73. A cylinder and a sphere roll down an incline starting at the same time. The one to reach the bottom first will be the

A) cylinder
B) sphere
C) neither; they both reach the bottom at the same time

Ooops! I did not give you the formulas for the "rotational mass" of the cylinder and sphere.

I(cylinder) = (1/2) m r ²

I(sphere) = (2/5) m r²

These "rotational masses" are given in Paul Hewitt's book and in the online notes.

Since the sphere has a smaller "rotational mass" it will be easier to rotate and will accelerate faster.

So the sphere will get to the bottom first.

However, since I did NOT include the "rotational masses" for these object, everyone gets credit for this question.

74. Put a pipe over the end of a wrench when trying to turn a stubborn nut on a bolt, to effectively make the wrench handle twice as long, you'll increase the torque by

A) two

"Rotational force" = force x moment arm

B) four
C) eight
D) sixteen

75. When a twirling ice skater extends her arms outward, her rotational speed

A) increases
B) decreases

As she extends her arms, her "rotational mass" increases.

Her angular momentum remains constant.

I = I

C) remains the same (or is conserved).

76. To turn a stubborn screw, it is best to use a screwdriver that has a handle that is

A) long and thin
B) thick or wide
C) yellow
D) slippery

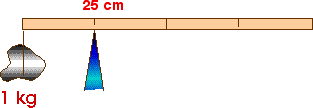
77. A 1-kg rock is suspended from the tip of a meter stick at the 0- cm mark so that the meter stick balances like a see-saw when the fulcrum is at the 25-cm mark. From this information, what is the mass of the meter stick?

A) 0.25 kg
B) 0.50 kg
C) 1.00 kg.
D) 2.00 kg

 
78. A car travels in a circle with constant speed. The net force on the car is

A) directed forward, in the direction of travel.
B) directed towards the center of the curve

This net force is also know as the "centripetal force".

C) zero because the car is not accelerating.
D) directed outward, away from the center of the curve

79. A driver tries to travel in a circle with constant speed. Due to water on the pavement, the force of friction is reduced. This causes the car to

A) travel in a circle of greater radius.

F = m v ²/ r

The mass m does not change.

If v does not change, then a smaller force F requires a greater radius r.

B) travel in a circle of smaller radius.
C) suddenly have a greater speed.
D) suddenly have a smaller speed.

 
80. One end of a long uniform log is raised to shoulder level. Another identical log is raised at its center to the same level. Raising the second log requires about

A) half as much work
B) the same work
C) twice as much work

| Return to Excursions Calendar |

(C) 2003, Doug Davis; all rights reserved