3050Ex1Sp00

Excursions in Physics
PHY 3050C
First Hour Exam

February 10, 2000

Enter all your answers in the "scantron sheet" or the "bubble sheet". Turn in only that sheet. Anything you write on this exam will not be seen or used or considered or graded. Be sure your name and SSN are on the "bubble sheet" you hand in. Be sure your name and SSN are bubbled-in. Be sure your answers are recorded correctly.

For every question, also consider the following as a possible answer:
e) none of the above

Possibly useful information:
v = ^x/ _t
a = ^v / _t
v = v_i + a t
x = x_i+ v_i t + (¹/₂) a t²
v = r w
F = m a
F₁₂ = - F₂₁
w = mg
g = 9.8 m/s² 10 m/s²

For every question, also consider the following as a possible answer:
e) none of the above

1. Kinematics is a description of motion. Motion was first well understood

a) by Henry Cavendish during the Industrial Revolution
b) by Aristotle and the ancient Greeks during the Golden Age
c) by Ptolemy in Egypt during the Ramses Dynasty
d) by Galileo in Italy during the Renaissance

2. Galileo was given a lifetime pension by the “city fathers” of Venice because he introduced

a) the pendulum clock
b) the water clock
c) the telescope
d) the sun dial

3. Galileo took a position as a professor of mathematics and taught

a) Euclid’s geometry
b) Newton’s differential calculus [ Newton was born the year Galileo died. ]
c) von Liebnitz’ integral calculus [ von Liebnitz was a contemporary of Newton's. ]
d) Rubick’s cubism [ Rubick's Cube is from the twentieth century. ]

4. Velocity is the time rate of change of

a) acceleration
b) speed
c) displacement
d) momentum

5. Acceleration is the time rate of change of

a) velocity
b) displacement
c) distance
d) momentum

6. Acceleration might be described as telling

a) where an object is located relative to an origin or reference point.
b) how fast something is moving.
c) how fast something is getting faster.
d) how long an object has been moving.

7. What is the average speed of a car that travels 125 km in 5 h?

a) 625 km/h
b) 25 km/h
v = dist/time
v = 125 km / 5 h

v = 25 km/h

c) 10 km/h
d) 9.8 km/h

8. Consider a train that has an acceleration of 3 m/s². Initially, at time t = 0, it has a velocity of v_i= 20 m/s. What is its speed at t = 3 s?

a) 57 m/s
b) 41 m/s
c) 29 m/s
v = v_i + a t
v = ( 20 m/s ) + ( 3 m/s² ) ( 3 s )

v = 20 m/s + 9 m/s

v = 29 m/s

d) 9 m/s

9. Consider a car that starts at rest and accelerates at 2 m/s² for 3 seconds.
At that time, t = 3 s, how fast is it going?

a) 18 m/s
b) 12 m/s
c) 9 m/s
d) 6 m/s
v = v_i + a t
v = ( 0 ) + ( 2 m/s² ) ( 3 s )

v = 0 + 6 m/s

v = 6 m/s

10. Consider a car that starts at rest and accelerates at 3 m/s² for 4 seconds.
At that time,, t = 3 s, how far has it gone?

a) 48 m
b) 24 m
x = x_i + v_i t + (¹/₂) a t²
x = 0 + 0 + (¹/₂) ( 3 m/s² ) ( 4 s )²

x = (¹/₂) ( 3 ) ( 16 ) m

x = 24 m

c) 12 m
d) 6 m

11. Consider a ball that is thrown upward at the edge of a canyon with an initial velocity of 20 m/s. Three seconds later, what is its velocity?

a) 30 m/s
b) 15 m/s
c) - 10 m/s
v = v_i + a t
v = ( 20 m/s ) + ( - 10 m/s² ) ( 3 s )

v = ( 20 - 30 ) m/s

v = - 10 m/s

d) - 30 m/s

12. Consider a ball that is thrown straight upward at the edge of a canyon with an initial velocity of 20 m/s. Three seconds later, where is it located? Take its initial position, at the edge of the canyon, to be the origin; that is, y_i= 0.

a) 30 m
b) 15 m
y = y_i + v_yi t + (¹/₂) a_y t²
y = 0 + ( 20 m/s ) ( 3 s ) + (¹/₂) ( - 10 m/s² ) ( 3 s )²

y = [ ( 20 ) ( 3 ) - (¹/₂) ( 10 ) ( 9 ) ] m

y = [ 60 - 45 ] m

y = 15 m

c) - 10 m
d) - 30 m

13. A rock climber dislodges a rock and notices that it falls for 6 seconds before hitting the canyon floor below. How fast is it going when it strikes the canyon floor?

a) 10 m/s
b) 15 m/s
c) 30 m/s
d) 60 m/s
v = v_i + a t
v = ( 0 ) + ( - 10 m/s² ) ( 6 s )

v = - 60 m/s

The minus sign simply means it is moving DOWN.

14. A rock climber dislodges a rock and notices that it falls for 6 seconds before hitting the canyon floor below. How far has it fallen when it strikes the canyon floor?

a) 10 m
b) 60 m
c) 180 m
y = y_i + v_yi t + (¹/₂) a_y t²
y = 0 + 0 + (¹/₂) ( - 10 m/s² ) ( 6 s )²

y = [ - (¹/₂) ( 10 ) ( 36 ) ] m

y = - 180 m

Again, the minus sign simply means it is BELOW where it started.

d) 360 m

15. Consider a ball that is thrown horizontally from the edge of a building with an initial velocity of 20 m/s. The ball is thrown 5 m above the driveway below. How far from the building does the ball strike the driveway?

a) 5 m
b) 10 m
c) 15 m
d) 20 m

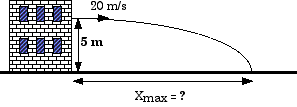
Before we can answer "How far?" we must first find out "How long?"
y = y_i + v_yi t + (¹/₂) a_y t²
0 = 5 m + 0 + (¹/₂) ( - 10 m/s² ) ( t )²

0 = 5 m + 0 + ( - 5 m/s² ) ( t )²

( 5 m/s² ) ( t )² = 5 m

( t )² = 1 s²

t = 1 s

The ball is in the air for one second. How far does it travel horizontally in that time?

x = x_i + v_x t
x = 0 + ( 20 m/s ) ( 1 s )

x = 20 m

16. Projectile motion is a combination of

a) horizontal motion with constant, non-zero acceleration and vertical motion with constant veloci
b) horizontal motion with constant non-zero acceleration and vertical motion with constant, non-zero acceleration
c) horizontal motion with constant velocity and vertical motion with constant, non-zero acceleration.
d) horizontal motion with constant velocity and vertical motion with constant velocity

17. Consider a ball thrown from a level surface with an initial upward velocity of 20 m/s and an initial horizontal velocity of 7 m/s. How long is the ball in the air?

a) 1.0 s
b) 2.0 s
c) 4.0 s
y = y_i + v_yi t + (¹/₂) a_y t²
0 = 0 + ( 20 m/s ) t + (¹/₂) ( - 10 m/s² ) ( t )²

0 = 0 + 20 t - 5 t²

5 t² - 20 t = 0

( 5 t ) ( t - 4 ) = 0

Either

5 t = 0
t = 0

While this is true, t = 0 is not very "interesting".

or

t - 4 = 0
t = 4 s

We could also have arrived at this time of t = 4 s just by looking at the velocity at the end of every second.

For t = 0, v = 20 m/s
for t = 1 s, v = 10 m/s

for t = 2 s, v = 0

for t = 3 s, v = - 10 m/s

for t = 4 s, v = - 20 m/s

When the speed is the same (20 m/s), the ball is back at its starting place.

Either way, we know the ball takes four seconds to get back to its initial position, the level surface from which it was thrown.

d) 8.0 s

18. Consider a ball thrown from a level surface with an initial upward velocity of 10 m/s and an initial horizontal velocity of 7 m/s. Where does it land? That is, measured from its initial position, where does it come back to and strike the level surface?

a) 7 m
b) 14 m
c) 28 m
d) 56 m

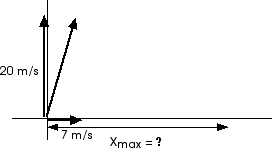
From the previous question we know the ball will be in the air for four seconds. How far does it move -- that is, how far, horizontally, does it move -- during that time?
x = x_i+ v_x t

Remember, a_x = 0; there is no horizontal acceleration.

x = x_i+ v_x t
x = 0 + (7 m/s)(4 s)

x = 28 s

19. Consider two children on a playground merry-go-round. One is near the center and one is near the edge. The child near the edge

a) requires more time to make one revolution than
b) travels slower than
c) requires less time to make one revolution than
d) makes one revolution in the same time as

the child near the center.

20. If a Ferris wheel has a radius of 10 m and requires 20 seconds to make a revolution, what is the linear speed of a passenger? C = 2 r; = 3.14

a) 0.78 m/s
b) 1.57 m/s
c) 3.14 m/s
d) 9.80 m/s
Due to the typo, this questions was not counted.

The 2 in C = 2 r was missing in the printed, hard-copy version of this exam.

Solution:

v = dist / time
v = C / time

v = 2 r / 20 s

v = [ (2)(3.14)(10) / 20 ] [m/s]

v = 3.14 m/s

21. Newton's First Law of Motion states that, in the absence of a net force, an object in motion will

a) eventually come to rest
b) continue in motion but slow down until it stops
c) continue in motion with the same speed along the same straight line
d) continue along the same straight line with a decrease in speed

22. Newton's Second Law of Motion explains the cause of motion and may be stated as

a) "All motion is relative."
b) "All objects fall with the same velocity."
c) "The acceleration of an object is proportional to the net force on the object and inversley proportional to the object's mass."
a = F / m
F = ma

d) "The acceleration of an object is proportional to the product of the object's mass and the net force on it."

23. Newton's Second Law of Motion explains the cause of motion and may be stated as

a) The net force on an object is inversely proportional to its weight.
b) The net force on an object produces an acceleration that is proportional to the time of action of that force.
c) The net force on an object is equal to the product of the mass of that object and its acceleration.
F = ma

d) The net force on an object is inversely proportional to the mass of the object.

24. Mass is a measure of

a) the volume of an object
b) the size of an object
c) how difficult it is to change the motion of an object
d) the velocity of an object

25. The weight of an object is

a) the same thing as the mass of an object
b) the sum of all the forces on an object
c) the force of gravity on an object
d) always less than the mass, even in a vacuum

26. The net force on a 10-kg object, at rest, is

a) 98 N
b) 49 N
c) 10 N
d) zero
The net force on any object at rest is zero!

27. The net force on a 10-kg object, in free fall, is

a) 98 N
w = m g
w = (10 kg)(9.8 m/s²)

w = 98 N

b) 49 N
c) 10 N
d) zero

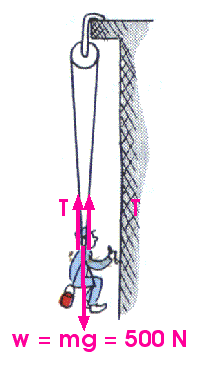
28. Harry the Painter has a weight of 500 N. When he is suspended as shown in the sketch here, what is the tension in the rope?

a) 1000 N
b) 500 N
c) 250 N
d) 25 N

29. A force of 24 N acts on an object whose mass is 8 kg. This causes the object to accelerate at

a) 2 m/s²
b) 3 m/s²
F = m a
24 N = ( 8 kg ) ( a )

24 N = ( 8 kg ) ( 3 m/s² )

a = 3 m/s²

c) 6 m/s²
d) 12 m/s²

30. A car, with mass of 1,000 kg, accelerates at 3 m/s².
The net force exerted on the car must be

a) 333 N
b) 1,000 N
c) 2,000 N
d) 3,000 N
F = m a
F = ( 1000 kg ) ( 3 m/s² )

31. The weight of a 1,000-kg car is

a) 500 N
b) 1,000 N
c) 2,000 N
d) 10,000 N
w = m g
w = (1,000 kg)(10 m/s²)

w = 10,000 N

32. What is the mass of a fireman whose weight is 500 N?

a) 9.8 kg
b) 25 kg
c) 50 kg
d) 500 kg
w = m g
500 N = m ( 10 m/s² )

500 N = ( 50 kg ) ( 10 m/s² )

m = 50 kg

33. A fireman, whose weight is 500 N, slides down a pole with an acceleration of 2 m/s². The forces that act on him are his weight pulling him down and the force of friction pulling up on him to slow him down. The force of friction must be

a) 50 N
b) 100 N
c) 400 N
F = m a
F_net = m a

F_net = ( 50 kg) ( 2 m/s² )

F_net = 100 N

F_net = w - F_friction

F_net = 500 N - F_friction

100 N = 500 N - F_friction

F_friction = 400 N

d) 500 N

34. Suppose you are driving along in an open car and throw a ball straight up into the air. While the ball is still in the air you step on the brakes. Where does the ball land relative to the car?

a) behind the car
b) back into the car
c) in front of the car
The ball continues on with the same horizontal velocity. It continues on and lands where the car would have been if you had not stepped on the brakes. But the car has slowed down so the ball ends up in front of the car.

35. If a sailor drops a wrench from the top of a tall mast on a moving ship, it will fall and hit the deck

a) in front of the base of the mast.
b) at the base of the mast.
Think back to my demonstration and to the movies from "The Mechanical Universe".

c) behind the base of the mast.

36. Sir Isaac Newton

a) first discovered the Law of Falling Bodies while at the University of Pisa.
b) was a close friend of Liebnitz and encouraged his early development of calculus.
c) made great advances in Mechanics, Gravity, Optics, and Mathematics.
d) used water clocks of his own invention to aid sailors in determining their longitude.

37. Galileo

a) may be called the Father of Modern Optics.
b) wrote his findings in Polish while at the University of Paduah.
c) may be called the Father of Modern Science.
d) wrote his findings about Gravity and explained calculus.

38. The hallmark of Modern Science is that

a) theories are accepted or rejected based upon the background or reputation of the scientists who propose them.
b) predictions of theories must be tested by and agree with experimental results.
c) theories must have elegant mathematical equations.
d) predictions of theories must not contradict established authorities (such as Plato or Pythagores).

39. When applying Newton's Second Law of Motion, F = ma,

a) F is always the largest force present.
b) F is always the net force -- or the sum of all the forces present.
c) m is always the largest mass in the system.
d) m must be the smallest mass in the system.

40. What value will the spring scale read in the system shown here?

a) zero
b) 50 N
c) 100 N
d) 200 N

41. In the sketch here, what value will the scale read if the little girl’s weight is 250 newtons.

a) zero
b) 125 N
c) 250 N
d) 500 N

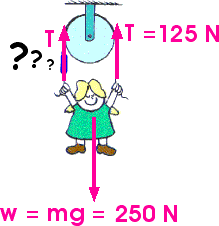
42. The four fundamental forces are

a) gravity, friction, electricity, and atomic
b) gravity, electromagnetic, strong nuclear, and weak nuclear
c) gravity, strong electric, weak electric, and atomic
d) gravity, friction, air resistance, and atomic

43. Which of the following has the largest momentum relative to Earth?

a) a tightrope walker crossing Niagara Falls.
b) a truck speeding along a highway.
Momentum = ( mass ) ( velocity )

c) a Mack truck sitting in the parking lot.
d) the Science building on campus.

44. A moving object on which no forces are acting will continue to move with constant

a) acceleration
b) impulse
c) momentum
d) all of these

45. Conservation of momentum is directly related to

a) Newton's First Law of Motion
b) Newton's Second Law of Motion
c) Newton's Third Law of Motion
F₁₂ = - F₂₁

d) International shortages of momentum

46. A rifle recoils from firing a bullet. The speed of the rifle's recoil is small because the

a) force against the rifle is smaller than against the bullet.
b) momentum of the rifle is smaller than that of the bullet.
c) mass of the rifle is much larger than the mass of the bullet.
d) momentum of the rifle is larger than that of the bullet.

47. A 5 kg ball has a momentum of 30 kg m/s. What is the ball's speed?

a) 3 m/s
b) 6 m/s
Momentum = ( mass ) ( velocity )
30 kg m/s = ( 5 kg ) ( velocity )

30 kg m/s = ( 5 kg ) ( 6 m/s )

v = 6 m/s

c) 15 m/s
d) 150 m/s

48. If two objects collide and do not stick together, their total momentum after the collision is

a) less than
b) the same as
Momentum is always conserved.

c) greater than

their total momentum before the collision.

49. If two objects collide and stick together, their total momentum after the collision is

a) less than
b) the same as
Momentum is always conserved.

c) greater than

their total momentum before the collision.

50. When two objects collide and stick together, this type of collision is known as a totally

a) elastic collision.
b) inelastic collision.
Kinetic energy will not be conserved, but
momentum is always conserved.

c) natural collision.
d) impulsive collision.

| Back to Excursion's Calendar |

(C) 2003, Doug Davis; all rights reserved.