Ex 10.3 How does the downward componenet of a projectile's motion compare to vertical free fall?
The downward component of a projectile's motion is free fall (that is, it is exactly the same as free fall).
Ex 10.6 A friend claims that bullets fired by some high-powered rifles trave for many meters in a straight line path without dropping. Another friend disputes this claim and states that all bullets fromany rifle drop beneath a straight-line path a vertical distance given by 1/2 g t2 and that the curved path is apparent at low velocities and less apparent at high velocities. Now it's your turn: Will all bullets drop the same vertical distance in equal times? Explain.
Your second friend is correct. Everything is affected by gravity and falls with an acceleration g so its vertical distance changes by 1/2 g t2. If its horizontal velocity is low this is easy to see and if its horizontal velocity is high, as with a high-powered rifle, this effect is less apparent and we must be more careful with our experiments to show it. But the effect is present, nonetheless.
Ex 10.10 A park ranger shoots a monkey hanging from a branch of a tree with a tranquilizing dart. The ranger aims directly at the monkey, not realizing that the dart will follow a parabolic path and thus fall below the monkey. The monkey, however, sees the dart leave the gun and lets go of the branch to avoid being hit. Will the monkey be hit anyway? Does the velocity of the dart affect your answer, assuming it is great enough to travel the horizontal distance to the tree before hitting the ground?
As we discussed and demonstrated in class, think of the motion of both dart and monkey if we could somehow turn gravity "off" and fire the dart. Then the dart would move along a straight line and hit the monkey who would remain in place beside the tree branch. Now turn gravity back "on" and fire the dart. Now both dart and monkey fall from their "gravity-off positions" by 1/2 g t2 so the monkey will, again, be hit by the dart.
Ex 10.15 Since the moon is gravitationally attracted to Earth, why doesn't it simply crash into Earth?
The moon is moving and the force that Earth exerts on the moon keeps it moving in a circle around Earth. If we could turn gravity "off", the moon would move off in a straight line instead of moving in a circle. We will return to this question as we look at Newton's Laws of Motion.
| Back to 3050's Home Page | Back to Calendar | ToC, Ch 10 | Periodic Motion |
Pb 10.5 John and Tracy look from their 80-m high-rise balcony to a swimming pool below--not exactly below, but, rather, 20 m from the bottom of their building. They wonder how fast they would have to jump horizontally to suceed in reaching the pool. What is your answer?
How long will it take to fall the vertical distance of 80 m? That time can be found from 1/2 g t2.1/2 g t2 = 80 m 1/2 (10 m/s2) t2 = 80 m
5 t2 = 80
t2 = [ 80 / 5 ] s2 = 16 s2
t = 4 s
Now, what must be the horizontal speed, vo, in order to travel the horizontal distance of 20 m to reach the pool in that time,
vo = x /
vo = 20 m / 4 s
vo = 5 m/s
Our high-rise daredevils must leave their window with an initial horizontal velocity of 5 m/s in order to reach the pool by the time they reach ground level.
Ex 10.* If you are standing in a bus that moves at constant velocity and drop a ball from your outstretched hand, you'll see its path as a vertical straight line. How will the path appear to a friend standing at the side of the road?
The path will be that of projectile motion, a parabola. The horizontal motion will be motion at constant speed -- the forward speed of the bus -- and the vertical motion will be motion at constant acceleration -- the free fall acceleration due to gravity, - 10 m/s2.
Ex 10.* Suppose you are driving along in an open car and throw a ball straight up into the air. While the ball is still in the air you step on the brakes. Where does the ball land relative to the car?
First, what happens when you drive along and remain at a constant velocity?
Then the ball falls back into the car. As you watch it from the car it goes straight up and comes back straight down. A friend on the sidewalk sees it move along a parabolic path. The ball is traveling according to projectile motion -- with vertical motion that has constant acceleration ( ay = - 10 m/s2 ) and horizontal motion that has constant velocity ( ax = 0 ).
Now, what happens if you step on the brakes after you throw the ball straight up? The ball continues along exactly the same path as before. But you do not go as far forward as before so the ball lands ahead of you or in front of your car.
Ex 10.* When you throw a rock off a cliff, how do the horizontal components of its motion compare for all points along its trajectory?
The horizontal component of a rock thrown from a cliff is constant; it remains the same until the rock hits the canyon floor below.
Ex 10.* If you use large-diameter tires on your car, how will your speedometer reading differ (a speedometer really reads the rpm's of the wheels).
As the tires move through one revolution, the car moves forward a distance equal to the circumference of the tire, C = pi d = (pi) x (diameter). If large-diameter tires are used, this distance will be greater than the speedometer was designed for so your car's speed will be greater than that indicated by the speedometer. Watch out for speeding tickets!
PB 10.* Calculate the ground velocity of an airplane that has an airspeed of 100 km/h when it is in a 100-km/h crosswind.
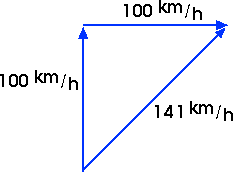You can find the ground speed of 141 km/h by making a careful diagram and measuring the length of this resultant vector.Or, you can find this ground speed numerically, . .
The two 100 km/h vectors form two sides of a right triangle. The ground speed is then the hypotenuse of this triangle. You can find its length by using the Pythagorean theorem,
hypotenuse = SQRT [ (side1)2 + (side2)2 ]hypotenuse = SQRT [ (100)2 + (100)2 ]
hypotenuse = SQRT [ 20 000 ]
hypotenuse = 141 km/hEx 10.* Suppose you swim in a direction directly across a flowing river and end up a distance downstream that is less than the width of the river. How does your swimming speed compare to the flow rate of the river?
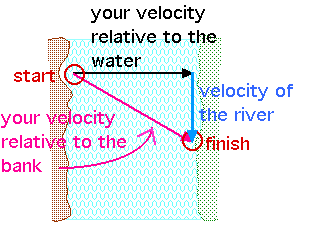From this diagram, we can see that your velocity, "your swimming speed", is greater than the speed of the river, "the flow rate of the river". This is because the distance downstream is less than the distance across the river.What would happen if your swimming speed were less? Then our diagram might look something like this:
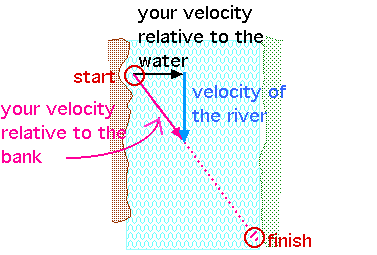
In this case, your distance downstream would be greater than the distance across the river.
PB 10.* Find the linear speed of a passenger on a Ferris wheel that has a radius of 10 m and rotates once in 30 seconds.
In one revolution, the passenger travels a linear distance equal to the circumference of the Ferris wheel,
distance = C = 2 pi r = 2 (pi) (radius)
distance = 2 (3.14) (10 m)
distance = 62.8 m This distance is covered in a time of t = 30 s, so the passenger's linear speed is
speed = distance / time
speed = 62.8 m / 30 s
speed = 2.1 m/s
| Back to 3050's Home Page | Back to Calendar | ToC, Ch 10 | Periodic Motion |
Typical multiple-guess questions
1. Consider a ball that is thrown horizontally from the edge of a building with an initial velocity of 20 m/s. The building is 5 m above the driveway below. How far from the building does the ball strike the driveway?
a) 5 mb) 10 m
c) 15 m
d) 20 m
2. When a ball or stone or other object is thrown or hit or fired, and air resistance can be neglected, the resulting motion is known as projectile motion The path of an object in projectile motion is
a) a straight lineb) a hyperbola
c) a parabola
d) a quadrant of a circle
3. Projectile motion is a combination of
a) horizontal motion with constant, non-zero acceleration and vertical motion with constant velocityb) horizontal motion with constant non-zero acceleration and vertical motion with constant, non-zero acceleration
c) horizontal motion with constant velocity and vertical motion with constant, non-zero acceleration
d) horizontal motion with constant velocity and vertical motion with constant velocity
4. Consider a ball thrown from a level surface with an initial upward velocity of 10 m/s and an initial horizontal velocity of 5 m/s. How long is the ball in the air?
a) 1.0 sb) 1.5 s
c) 2.0 s
d) 4.0 s
5. Consider a ball thrown from a level surface with an initial upward velocity of 10 m/s and an initial horizontal velocity of 5 m/s. Where does it land? That is, measured from its initial position, where does it come back to and strike the level surface?
a) 5 mb) 10 m
c) 15 m
d) 20 m
From the previous question, we already know the ball is in the air for t = 2 secx = vx t = (5 m/s) ( 2 s) = 10 m| Back to 3050's Home Page | Back to Calendar | ToC, Ch 10 | Periodic Motion |
Answers to the typical multiple-guess questions:
1. Consider a ball that is thrown horizontally from the edge of a building with an initial velocity of 20 m/s. The building is 5 m above the driveway below. How far from the building does the ball strike the driveway?
a) 5 mb) 10 m
c) 15 m
d) 20 m
y = (1/2) a t 2- 5 m = (1/2) ( - 10 m/s 2) t 2 = (- 5 m/s2) t 2
1 s2 = t2
t = 1 s
x = vx t = (20 m/s) (1 s) = 20 m
2. When a ball or stone or other object is thrown or hit or fired, and air resistance can be neglected, the resulting motion is known as projectile motion The path of an object in projectile motion is
a) a straight lineb) a hyperbola
c) a parabola
d) a quadrant of a circle
3. Projectile motion is a combination of
a) horizontal motion with constant, non-zero acceleration and vertical motion with constant velocityb) horizontal motion with constant non-zero acceleration and vertical motion with constant, non-zero acceleration
c) horizontal motion with constant velocity and vertical motion with constant, non-zero acceleration
d) horizontal motion with constant velocity and vertical motion with constant velocity
4. Consider a ball thrown from a level surface with an initial upward velocity of 10 m/s and an initial horizontal velocity of 5 m/s. How long is the ball in the air?
a) 1.0 sb) 1.5 s
c) 2.0 s
d) 4.0 s
Time to top: v = 0v = vi + a t = 10 m/s + ( - 10 m/s2) (ttop) = 00 = 10 - 10 t top
t top = 1 sec
Total time in the air
ttotal = 2 ttop = 2 s
5. Consider a ball thrown from a level surface with an initial upward velocity of 10 m/s and an initial horizontal velocity of 5 m/s. Where does it land? That is, measured from its initial position, where does it come back to and strike the level surface?
a) 5 mb) 10 m
c) 15 m
d) 20 m
From the previous question, we already know the ball is in the air for t = 2 secx = vx t = (5 m/s) ( 2 s) = 10 m| Back to 3050's Home Page | Back to Calendar | ToC, Ch 10 | Periodic Motion |
(C) 2003 Doug Davis, all rights reserved