

Satellite Orbits
In our text, the ninth edition of Paul Hewitt's Conceptual Physics, this topic of Satellite Orbits appears in the next chapter, Projectile Motion and Satellite Orbits. I think it fits better here. You can read about it in chapter 10 of Hewitt's text, however.
The only force on a satellite in orbit around our Earth is the force of gravity. Since this is the only force, it is certainly the net force. The net force on any object moving in a circle is also called the centripetal force, Fc. This centripetal force is directed toward the center and is equal to
Fc = m v2 / r
The only force on a satellite is the force of gravity. A satellite remains in orbit because this force of gravity provides the centripetal force necessary for it to move in a circle. Of course satellite orbits may be ellipses, but we will restrict our attention to satellites in circular orbits. This keeps the radius and the speed constant.
Fg = Fc We will look at two particular orbits. The Space Shuttle uses a low-Earth orbit in which it travels just above Earth's atmosphere. As you watch the Olympic Games, the signal is sent from China to a communications satellite and then re-transmitted to receivers in the United States. Such communications satellites appear to be stationary because they are in orbits with periods of 24 hours; these are called geosynchronous or geostationary orbits. These geostationary orbits are also directly over the equator.Fg = m v2 / r
Low-Earth Orbit
The Space Shuttle is an excellent example of a satellite in a low-Earth orbit. The Space Shuttle orbits about 300 km to 500 km above Earth's surface. Earth's radius is about 6 000 km so this is an increase of only about 5% or 8%. That means the force of gravity is only about 10% to 15% less than at Earth's surface.
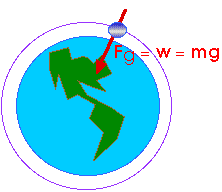
Therefore, we can use the approximation that the force of gravity is the same on the orbiting satellite as it is at Earth's surface. That is,
Fg = m g
Fg = m v2 / r
m g = m v2 / r
g = v2 / r
v2 = g r
We know the radius; to be in a low-Earth orbit, the radius of the orbit must be nearly equal to Earth's radius of about 6 000 km or 6 x 106 m. g is the acceleration of gravity at the surface of the Earth so we know g is about 10 m/s2. Of course, we could use 9.8 m/s2 but our entire calculation is a reasonable approximation so we will use 10 m/s2.
We could simply calculate the orbital velocity and we will do that. But it is also interesting -- and fairly easy -- to extend this and calculate the orbital period -- the time necessary for one orbit. But first, the orbital velocity.
v2 = g rv2 = ( 10 m/s2 ) ( 6 x 106 m ) = 6 x 107 (m/s)2
v = 7.7 x 103 m / s
That's a fine answer but most of us have little or no "intuitive feel" for how fast that really is. How fast is a thousand meters per second? How fast is ten thousand meters per second? Let's convert that to km/h -- or even to mph.
v = 7.7 x 103 m / s [ km / 1000 m ] [ 3600 s / h ] = 28 000 km / hv = 28 000 km / h [ mi / 1.61 km ] = 17 000 mi/h
What about the period? How long does it take to make one orbit?
v = D / TT = D / v
T = 2
r / v
T = 2 ( 3.14 ) ( 6 x 106 m ) / ( 7.7 x 103 m / s )
T = 4 900 s [ 1 min/60 s ] = 81 min
(Remember, we've made some approximations; the period of a low-Earth satellite is about an hour and a half).
From a NASA web site:How fast does a Space Shuttle travel? What is its altitude? How much fuel does it use?
Like any other object in low Earth orbit, a Shuttle must reach speeds of about 17,500 mph (28,000 kilometers per hour) to remain in orbit. The exact speed depends on the Shuttle's orbital altitude, which normally ranges from 190 miles to 330 miles (304 kilometers to 528 kilometers) above sea level, depending on its mission.
Many communications satellites use a booster rocket to go to an orbit 22,300 miles [35,680 kilometers] high. Known as geosynchronous orbit, this height is special because a satellite orbiting here circles the Earth at the same rate as a point on the equator, allowing it to hover over a ground station located at that point.
Each of the two Solid Rocket Boosters on the Shuttle carries more than one million pounds of solid propellant. The Shuttle's large External Tank is loaded with more than 500,000 gallons of supercold liquid oxygen and liquid hydrogen, which are mixed and burned together to form the fuel for the Shuttle's three main rocket engines.
Geo-synchronous Orbit"Tracking" a communications satellite docked in an equatorial orbit with a period of 24 h is far, far easier than tracking a satellite in a low-Earth orbit. "Tracking" such a communications satellite simply means pointing an antenna at the satellite and leaving it alone. A satellite in such an orbit appears to be stationary. Such an orbit is called geostationary or geosynchronous.

What orbital radius is required for such a geostationary satellite?
Fg = v2 / rHowever, we can no longer use an approximation like Fg = mg. Now we must use the "real" gravitational force,
Fg = G M m / r2Fg = m v2 / r
G M m / r2 = m v2 / r
G M / r2 = v2 / r
v = 2
r / T
G M / r2 = ( 2
r / T )2 / r
G M / r2 = ( 4
2r 2 / T 2 ) / r
G M / r2 = 4
2r 2 / T 2 r
G M / r2 = 4
2r / T 2
G M T 2 / 4
2 = r3
r3 = G M T 2 / 4
2
r3 = [ G M / 4
2] T 2
First, notice that this is Kepler's Third Law, r3 / T2 = constant.
Now we can plug in numbers and evaluate r
T = 24 h [ 3600 s / h ] = 86 400 s = 8.64 x 104 sM = MEarth = 6 x 1024 kg
G = 6.67 x 10-11 N kg2 / m2
r3 = [ ( 6.67 x 10-11 N kg2 / m2 ) ( 6 x 1024 kg ) / ( 4 ) ( 3.14 )2 ] [ 8.64 x 104 s ]2
r3 = 7.57 x 1022 m3
r = 4.23 x 107 m
r = 42 300 km
r = 42 300 km [ 0.61 mi / 1 km ] = 25 800 mi
[ You might ask why we did all this? You might ask why we went to this much trouble?
You have all the tools -- all the knowledge and skill -- needed to understand these two satellite orbits in detail. The next time you watch a television broadcast about the Space Shuttle or a broadcast from the other side of the Earth, smile a little. You understand the details. You don't really need to be a rocket scientist to understand this aspect of Rocket Science! ]
(c) Doug Davis, 2003; all rights reserved




Gravity Summary Return to ToC, Gravity