

Ch 9: Gravity; Ex 2, 12, 16, 17, 22, 39, 40 (Ch10.17); Pb 3
![]()
Ex 9.2 Gravitational force acts on all bodies in proportion to their masses. Why, then does not a heavy body fall faster than a light body?
F = m aWhile the gravitational force is, indeed, proportional to the mass of a falling object, that is precisely what we require to have a constant acceleration due to Newton's Second Law, F = m a.
Ex 9.12 The Earth and the Moon are attracted to each other by gravitational force. Does the more massive Earth attract the less massive Moon with a force that is greater, smaller, or the same as the force with which the Moon attracts the Earth?
(With a rubber band stretched between your thumb and forefinger, which is pulled more strongly by the band, your thumb or your forefinger?)
Remember Newton's Third Law, Action and Reaction, F12 = - F21 ?The force the Earth exerts on the Moon is exactly the same as the force the Moon exerts on the Earth (but they act in opposite directions).
Ex 9.16 A small light source located 1 m in front of a 1-m2 opening illuminates a wall behind. If the wall is 1 m behind the opening (2 m from the light source), the illuminated area covers 4 m2. How many square metters will be illuminated if the wall is 3 m from the light source? 5m? 10m?
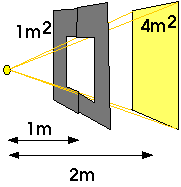
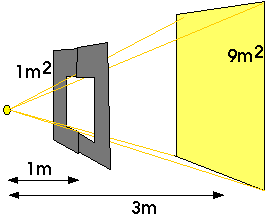
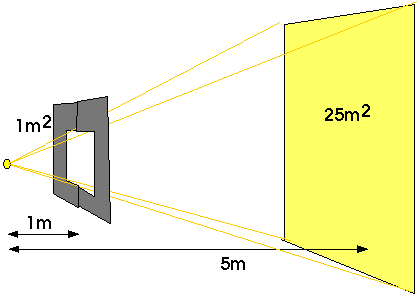
At 10 m, the area illuminated will be (10 m)2 = 100 m2
Ex 9.17 The planet Jupiter is more than 300 times as massive as Earth, so it might seem that a body on the surface of Jupiter would weigh 300 times as much as on Earth. But it so happens that a body would scarcely weigh three times more on the surface of Jupiter as it would on the surface of Earth. Can you think of an explanation for why this is so?
(Hint: Let the terms in the equation for gravitational force guide your thinking.)
F = G M m / R2 MJ = 300 ME
FJ = 3 FE
FJ = G MJ m / RJ2 = 3 [ G ME m / RE2 ] = 3 FE
FJ = G (300 ME) m / RJ2 = 3 [ G ME m / RE2 ] = 3 FE
G (300 ME) m / RJ2 = 3 [ G ME m / RE2 ]
(300 ME) / RJ2 = 3 [ ME / RE2 ]
(300 ) / RJ2 = 3 [ 1 / RE2 ]
100 / RJ2 = 1 / RE2
RJ2 / 100 = RE2
RJ2 = 100 RE2
RJ = 10 RE
The radius of Jupiter is about ten times as large as the radius of Earth!
Ex 9.22 If you were in a freely falling elevator and you dropped a pencil, you would see the pencil hovering. Is the pencil falling? Explain. Think of a glass elevator on the outside of a building -- so it can be seen easily and seen into easily.
It depends upon your "frame of reference". If you are falling along with the elevator, you will see the pencil hovering -- so it certainly isn't falling as you observe it. However, someone standing at rest on the Earth watching from the outside will see you, the elevator, and the pencil all to be falling.
Ex 9.39 If the Earth were of uniform composition, would your weight increase or decrease at the bottom of a deep mine shaft? Why?
For a uniform Earth, the force of gravity would decrease as we go below the surface. Therefore, your weight should be less at the bottom of a deep mine shaft.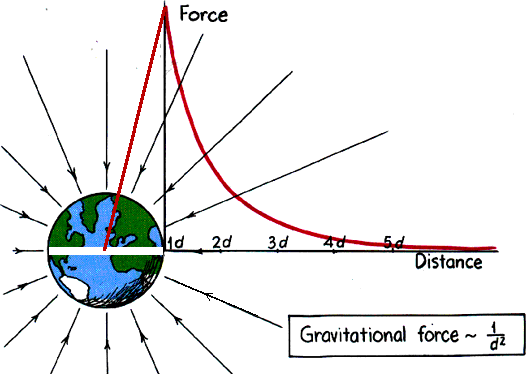
However, Earth does not have uniform density. The center of Earth is more dense than Earth's crust or outer layers. Therefore, as you go down in a deep mine, your weight actually increases!
Ex 9.40 It so happens that an actual increase in weight is found even in the deepest mine shafts. What does this tell us about the density of the Earth's composition?
However, . . . , your weight will actually increase! That means you are getting closer to more mass. That is, the outer layer of Earth has less density (less mass per volume) than the center. The center might be made of something like lead while the outer layers are of something like rock and soil.
From Chapter 10
Ex 10.17 Which planets, those closer to the Sun than the Earth or those farther from the Sun than the Earth, have a period greater than 1 Earth year?
Kepler's Third Law of Planetary Motion
T2 / R3 = constant means that the period increases as the radius increases. For the Earth, the period is exactly one Earth year! Planets with orbital radii greater than Earth's will have periods that are also greater than Earth's. Mars, Jupiter, and Saturn have periods greater than one Earth year. Planets with orbital radii smaller than Earth's will have periods that are also smaller than Earth's. Mercury and Venus have periods smaller than one Earth year.
Extra Exercise
Ex 9.X If the mass of the Earth somehow increased, with all other factors remaining the same, would your weight also increase?
(Hint: Let the equation for gravitational force guide your thinking.)
Increasing the mass of the Earth would increase the force of gravity on me and "the force of gravity on me" is my weight. That is, my weight would increase.
Calculational Problem
Pb 9.3 The value of g at Earth's surface is about 9.8 m/s2. What is the value of g at a distance from Earth's center that is 4 times Earth's radius?
The force of gravity is an inverse-square force. Earth's surface is one Earth radius away from Earth's center. So being 4 times Earth's radius away from the center means the force of gravity -- and the acceleration due to gravity -- will be 1/16 as great as it is on Earth's surface.g' = (1/16) (9.8 m/s2) g' = 0.61 m/s2
Extra Problem
Pb 9. X Saturn is approximately ten times as far from the Sun as the Earth's distance from the Sun. By way of Kepler's Third Law, estimate the approximate time in Earth years for Saturn to take to make one revolution about the Sun.
R S = 10 R E T2 / R3 = const
TS2 / RS3 = TE2 / RE3
TS2 / (10 RE)3 = TE2 / RE3
TS2 / (1,000 RE3) = TE2 / RE3
TS2 / (1,000) = TE2
TS2 = 1,000 TE2
TS = [SQRT (1,000) ] TE
TS = [31.6] TE
The period for Saturn is about 31.6 Earth years.
"SQRT" simply means "square root of"
but it is far easier for me to type!
| Back to Calendar | ToC, Ch 9 | Ch 10, Projectile Motion |
Typical or possible multiple-choice questions:
1. According to Kepler's laws, the paths of planets about the Sun are
A) straight linesB) parabolas
C) ellipses
D) hyperbolas
2. According to Newton, the greater the masses of interacting objects, the
A) greater the force of gravity, by the product of the massesB) less the force of gravity
C) greater the force of gravity, by the square of the masses
D) less the force of gravity, inversely as the square of the masses
3. According to Newton, the greater the distance between masses of interacting objects, the
A) greater the force of gravity, proportional to the distanceB) less the force of gravity, inversely as the distance
C) greater the force of gravity, proportional to the square of the distance
D) less the force of gravity, inversely as the square of the distance
4. What is the force of gravity on a 500-newton woman standing on the earth's surface?
A) 9.8 NB) 50 N
C) 500 N
D) 5,000 N
5. If the mass of the earth somehow increased with no change in radius, your weight would
A) increaseB) decrease
C) stay the same
D)
6. If the radius of Earth somehow decreased with no change in mass, your weight would
A) increaseB) decrease
C) stay the same
D)
7. If Earth's mass decreased to one-half its original mass with no change in radius, then your weight would
A) decrease to one-quarter its original valueB) decrease to one-half its original value
C) remain the same
D) increase to twice its original value
8. The force of gravity acting on the Space Shuttle in orbit is nearly
A) zeroB) equal to the weight of the Space Shuttle at Earth's surface
C) about one-tenth its weight at Earth's surface
D) about one-one hundredth its weight at Earth's surface
9. A woman who normally weighs 400 N stands on top of a very tall ladder so she is one earth radius above the earth's surface. How much would she weigh there?
A) zeroB) 100 N
C) 200 N
D) 400 N
10. The force of gravity acts on all apples on an apple tree. Some apples are twice as far from the ground as others. These twice- as-high apples, for the same mass, have practically
A) one-fourth the weightB) one-half the weight
C) the same weight
D) twice the weight
11. The planet Jupiter is about 300 times as massive as Earth, yet on its surface you would weigh only about 3 times as much. This is because
A) your mass is 100 times less on Jupiter.B) Jupiter is significantly farther from the sun.
C) Jupiter's radius is 10 times Earth's radius.
D) you are 100 times more weightless there.
| Back to Calendar | ToC, Ch 9 | Ch 10, Projectile Motion |
Answers to typical or possible multiple-choice questions:
1. According to Kepler's laws, the paths of planets about the Sun are
A) straight linesB) parabolas
C) ellipses
D) hyperbolas
2. According to Newton, the greater the masses of interacting objects, the
A) greater the force of gravity, by the product of the massesF = G M m / d2B) less the force of gravity
C) greater the force of gravity, by the square of the masses
D) less the force of gravity, inversely as the square of the masses
3. According to Newton, the greater the distance between masses of interacting objects, the
A) greater the force of gravity, proportional to the distanceB) less the force of gravity, inversely as the distance
C) greater the force of gravity, proportional to the square of the distance
D) less the force of gravity, inversely as the square of the distance
F = G M m / d2
4. What is the force of gravity on a 500-newton woman standing on the earth's surface?
A) 9.8 NB) 50 N
C) 500 N
D) 5,000 N
5. If the mass of the earth somehow increased with no change in radius, your weight would
A) increaseF = G M m / d2B) decrease
C) stay the same
D)
6. If the radius of Earth somehow decreased with no change in mass, your weight would
A) increaseF = G M m / d2B) decrease
C) stay the same
D)
7. If Earth's mass decreased to one-half its original mass with no change in radius, then your weight would
A) decrease to one-quarter its original valueB) decrease to one-half its original value
F = G M m / d2C) remain the same
D) increase to twice its original value
8. The force of gravity acting on the Space Shuttle in orbit is nearly
A) zeroB) equal to the weight of the Space Shuttle at Earth's surface
F = G M m / d2In a low-Earth orbit, the Space Shuttle's distance from the center of Earth is nearly the same as it was at Earth's surface.
C) about one-tenth its weight at Earth's surface
D) about one-one hundredth its weight at Earth's surface
9. A woman who normally weighs 400 N stands on top of a very tall ladder so she is one earth radius above the earth's surface. How much would she weigh there?
A) zeroB) 100 N
F = G M m / d2If d is made twice as large, then d2 will be four times as large. Since we are dividing by d2, this means the Force -- her weight -- will be only one-fourth as much.
C) 200 N
D) 400 N
10. The force of gravity acts on all apples on an apple tree. Some apples are twice as far from the ground as others. These twice- as-high apples, for the same mass, have practically
A) one-fourth the weightB) one-half the weight
C) the same weight
F = G M m / d2Being twice as far above the ground has hardly any effect on d, the distance from the center of Earth to the apple.
D) twice the weight
11. The planet Jupiter is about 300 times as massive as Earth, yet on its surface you would weigh only about 3 times as much. This is because
A) your mass is 100 times less on Jupiter.B) Jupiter is significantly farther from the sun.
C) Jupiter's radius is 10 times Earth's radius.
D) you are 100 times more weightless there.
| Back to Calendar | ToC, Ch 9 | Ch 10, Projectile Motion |
(C) 2003, Doug Davis; all rights reserved