Excursions in Physics

Homework, Chapter 7: Energy

Ch 7, Energy; Ex 4, 7, 13, 14, 44, 46; Pb 2, 6

Exercises (Discussion Questions)

Ex7.4 When a rifle with a long barrel is fired, the force of expanding gases acts on the bullet for a longer distance. What effect does this have on the velocity of the emerging bullet? (Do you see why long-range cannons have such long barrels?)

Work = force x distance

work = change in KE = change in [ ¹/₂ m v² ]

The expanding gases exert a force on the bullet. This force is exerted over a distance so work is done on the bullet. This work done on the bullet means its KE (kinetic energy) increases. If the distance over which the force acts increases, then the amount of work done on the bullet increases and the final value of its KE increases -- more KE means more speed! Long-rang cannons on naval ships are 10 or 15 meters long.

Ex 7.7 Can something have energy without having momentum? Explain. Can something have momentum without having energy? Defend your answer.

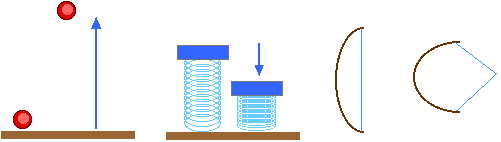
An object at rest has no momentum; its velocity is zero. But it can still have potential energy -- PE -- because of work we have done on it. We can lift an object and give it gravitational PE = m g h. It has PE because it can do work on something else as it falls -- or it can increase its own KE. Lifting the object, to give it PE, requires that work be done on it. If we compress a spring, we must do work on it. That work is then stored in the compressed spring and is available to do work on something else. That means there is PE stored in a compressed spring. If we bend a bow we must do work on it. That work is then stored in the bent bow and is available to do work on something else. That means there is PE stored in a bent bow. In all these cases, on object can have energy -- potential energy -- even though it is at rest; an object at rest has no momentum.

However, if an object has momentum it has a velocity. And, if it has a velocity, it has KE -- kinetic energy or energy of motion. So, if an object has momentum, it must also have energy.

Ex 7.13 At what point in its motion is the KE of a pendulum bob a maximum? At what point is its PE a maximum? When its KE is half its maximum value, how much PE does it have?

The KE of a pendulum is maximum at the bottom of its swing where its PE is minimum (or where we often take its PE to be zero).

The PE of a pendulum is maximum at the top of its swing where it momentarily stops and its KE is zero.

The total energy remains constant,

E = KE + PE

So when the pendulum's KE is half its maximum value, its PE is half its maximum value if we have counted its PE as zero at the bottom of its swing.

 

Ex 7.14 A Physics instructor demonstrates energy conservation by releasing a heavy pendulum bob, as shown in the sketch, allowing it to swing to and fro. What would happen if, in his exuberance, he gave the bob a slight shove as it left his nose? Why?

Ouch!

If the bob starts off from rest, it will convert its PE into KE going down to the bottom of the swing and then convert KE back to PE and come to rest at the other end of its swing and then start back. On the way back, it increases its KE by reducing its PE until it comes to the bottom of the swing. On the last part of its swing, this KE decreases as it rises and increases its PE until the KE finally goes to zero and the pendulum comes to rest. With KE = 0, the PE must be equal to the total energy which is the original PE and it is back at its original height.

However, if the bob starts off with some KE because of a shove, then its total energy is greater than for the case just described. At the bottom of its swing, the pendulum will have a greater speed due to this increased energy. At the other end of the swing, it will come to rest at a greater height so its PE is greater. On the way back, that great height means it will smash our exuberant physicist in the nose!

Ouch!

Ex 7.44 Scissors for cutting paper have long blades and short handles, whereas metal-cutting shears have long handles and shout blades. Bolt cutters have very long handles and very short blades. Why is this so?

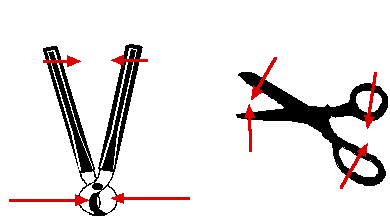
Scissors are levers. A longer blade with the short handles means that the longer blade moves a greater distance but with less force when compared to the handles. Metal-cutting shears have blades that move a smaller distance but with more force. The bolt cutters, with very short blades and very long handles, have blades that move and even smaller distance but with even greater force. Input work is done by the "operator" as she or he exerts a force on the handles and moves them through a distance. Output work is done by the blade as it exerts a force and moves through a distance. These devices trade off moving a small force through a large distance, as with the scissors, or moving a greater force through a smaller distance.

Ex 7.44 Consider the swinging-balls apparatus, also known as Newton's pendulum. If two balls are lifted and released, momentum is conserved as two balls pop out the other side with the same speed as the released balls at impact. But momentum would also be conserved if one ball popped out at twice the speed. Can you explain why this never happens? (And why is this exercise in Chapter 6, on Energy, rather than Chapter 5, on Momentum?)

Indeed, momentumwould be conserved if a single ball popped out with twice the original, incoming speed. We might write that as initial momentum = (2 m) (v_o) = (m) (2 v_o) = final momentum

But what does that do to the KE? Remember that KE = (¹/₂) m v²

initial KE = 2 [ (¹/₂) m v_o² ] =?= 1 [ (¹/₂) m (2 v_o)² ] = final KE

initial KE = 2 [ (¹/₂) m v_o² ] =?= 1 [ (¹/₂) m (4 v_o² )] = final KE

initial KE = 2 [ (¹/₂) m v_o² ] =?= 4 [ (¹/₂) m v_o² ] = final KE

initial KE = 2 [ (¹/₂) m v_o² ] =/= 4 [ (¹/₂) m v_o² ] = final KE

Because of the way KE is defined, this situation would make the final KE twice as much as the initial KE. So this doe not happen!

Work done by the brakes changes the car's KE from its initial value to zero. This work is equal to the force of friction causing the skid marks multiplied by the length of the skid marks since work = force x distance

When the car's speed is increased from 50 km/h to 150 km/h, its KE is increased by nine times! Remember that KE is given by

KE = (¹/₂) m v²

so increasing v by three means that KE increases by nine. The force of friction between the road and the skidding tires does not change appreciably so the distance or length over which the force is applied must increase nine times as well. That means we would expect skid marks to be about 9 x 15 m or 135 m long.

 

Pb 7.6 Consider the inelastic collision between the two freight cars in the last chapter (Figure 6.11). The momentum before and after the collision is the same. The KE, however, is less after the collision than before the collision. How much less, and what becomes of this energy?

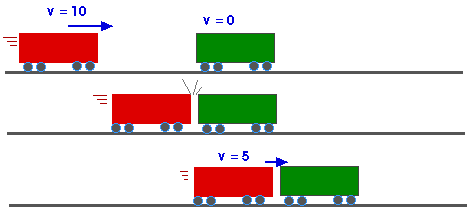
momentum = mass x velocity

The two freight cars have the same mass -- just call it M -- so the momentum is conserved. We can see that from

initial momentum = M (10) + M (0) = M (10)

initial momentum = M (10) = (2 M) (5) = final momentum

But what has happened to the KE?

initial KE = (1/2) M v_o² = (1/2) M (10)² = (1/2) M (100)

(1/2) M_total v_f² = (1/2) (2 M) (5)² = (1/2) M (50) = final KE

initial KE = 2 x final KE

The final Kinetic Energy is only one-half the initial Kinetic Energy (even though the final momentum is equal to the initial momentum). In an accidental collision, kinetic energy will be "lost" (that is, converted into heat) by bending and breaking parts of the cars. In a designed collision, like this, kinetic energy will be "lost" (or turned into heat) by heating up the couplings that hold the cars together.

Here's an "extra" one.

Pb 7.* Your monthly electric bill is probably expressed in kilowatt-hours (kWh), a unit of energy delivered by the flow of 1 kW of electricity for 1 hr. How many joules of energy do you get when you buy 1 kWh?

1 watt = 1 W = 1 J/s

Therefore,

1 J = (1 W) x (1 s) = (1 W) (1 s) = 1 W s

1 kWh = [1 kW] [ h ]

1 kWh = [1 kW (^{1000 W} /_kW)] [ h (^{60 min}/_h) (^{60 s}/_min)] = 3,600,000 Ws = 3,600,000 J

1 kWh = 3,600,000 J

| Back to 3050's Home Page | Back to Calendar | ToC, Ch 7 | Ch 8, Rotation |

Typical or possible multiple-guess questions for this material:

1. If you push an object twice as far while applying the same force you do

A) half as much work

B) the same amount of work

C) twice as much work

D) four times as much work

2. If you push an object just as far while applying twice the force you do

A) half as much work

B) the same amount of work

C) twice as much work

D) four times as much work

3. Exert 1 N for a distance of 1 m in 1 s and you deliver a power of

A) 0.5 W

B) 1.0 W

C) 2.0 W

D) 3.0 W

4. Exert 100 J in 50 s and your power output is

A) 0.5 W

B) 1.0 W

C) 2.0 W

D) 4.0 W

5. An object is raised above the ground gaining a certain amount of potential energy. If the same object is raised twice as high it gains

A) half as much energy

B) the same amount of energy

C) twice as much energy

D) four times as much energy

6. An object that has kinetic energy must be

A) elevated

B) falling

C) moving

D) at rest

7. An object that has potential energy may have this energy because of its

A) speed

B) acceleration

C) momentum

D) position

8. A clerk can lift containers a vertical distance of 1 meter or can roll them up a 2 meter-long ramp to the same elevation. With the ramp, the applied force required is about

A) one-fourth as much

B) half as much

C) the same

D) twice as much

9. When a car is braked to a stop, its kinetic energy is transformed to

A) energy of motion

B) heat energy

C) stopping energy

D) potential energy

10. For which position above does the ball on the end of the string have the greatest gravitational potential energy?

11. For which position above does the ball on the end of the string have the greatest kinetic energy?

12. Which requires more work: lifting a 5 kg sack vertically 2 meters or lifting a 10 kg sack vertically 4 meters?

A) lifting the 5 kg sack

B) both require the same amount of work

C) lifting the 10 kg sack

D) both require the same amount of force

13. A 10 kg sack is lifted 2 meters in the same time as a 5 kg sack is lifted 4 meters. The power expended in raising the 10 kg sack compared to the power used to lift the 5 kg sack is

A) half as much

B) the same

C) twice as much

D) four times as much

14. A 2 kg mass is held 4 m above the ground. What is the approximate potential energy of the mass with respect to the ground?

A) 8 J

B) 40 J

C) 80 J

D) 160 J

15. A 2 kg mass has 40 J of potential energy with respect to the ground. Approximately how far is it located above the ground?

A) 1 m

B) 2 m

C) 3 m

D) 4 m

16. Using 1,000 J of work, a model elevator is raised from the ground floor to the second floor in 20 seconds. How much power does the elevator use?

A) 50 W

B) 500 W

C) 2 kW

D) 20 kW

17. A car moves 4 times as fast as another identical car. Compared to the slower car, the faster car has

A) the same kinetic energy

B) 4 times the kinetic energy

C) 8 times the kinetic energy

D) 16 times the kinetic energy

18. A car moving at 50 km/hr skids 20 m with locked brakes. How far will the car skid with locked brakes if it is traveling at 150 km/hr?

A) 40 m

B) 60 m

C) 90 m

D) 180 m

19. When a rifle is fired it recoils so both the bullet and rifle are set in motion. The rifle and bullet ideally acquire equal but opposite amounts of

A) kinetic energy

B) momentum

C) potential energy

D) all of the above

20. What does an object have when moving that it doesn`t have when at rest?

A) momentum

C) mass

D) all of the above

21. If an object has kinetic energy, then it also must have

A) momentum

B) velocity

C) speed

D) all of the above

| Back to 3050's Home Page | Back to Calendar | ToC, Ch 7 | Ch 8, Rotation |

Answers to the typical or possible multiple-choice questions for this material:

1. If you push an object twice as far while applying the same force you do

A) half as much work

B) the same amount of work

C) twice as much work

W = F s

W = F s

D) four times as much work

2. If you push an object just as far while applying twice the force you do

A) half as much work

B) the same amount of work

C) twice as much work

W = F s

W = F s

D) four times as much work

3. Exert 1 N for a distance of 1 m in 1 s and you deliver a power of

A) 0.5 W

B) 1.0 W

Power is the rate at which work is done

P = W /t

P = [(1 N) ( 1 m)] / (1 s)

P = 1 J / 1 s

P = 1 W

C) 2.0 W

D) 3.0 W

4. Exert 100 J in 50 s and your power output is

A) 0.5 W

B) 1.0 W

C) 2.0 W

Power is the rate at which work is done

P = W / t

P = 100 J / 50 s

P = 2 W

D) 4.0 W

5. An object is raised above the ground gaining a certain amount of potential energy. If the same object is raised twice as high it gains

A) half as much energy

B) the same amount of energy

C) twice as much energy

PE = m g h

D) four times as much energy

6. An object that has kinetic energy must be

A) elevated

B) falling

C) moving

KE = (¹/₂) m v²

D) at rest

7. An object that has potential energy may have this energy because of its

A) speed

B) acceleration

C) momentum

D) position

8. A clerk can lift containers a vertical distance of 1 meter or can roll them up a 2 meter-long ramp to the same elevation. With the ramp, the applied force required is about

A) one-fourth as much

B) half as much

W_ramp = W_lift

F_ramp x 1 m = F_lift x 2m

F_ramp = (¹/₂) F_lift

C) the same

D) twice as much

9. When a car is braked to a stop, its kinetic energy is transformed to

A) energy of motion

B) heat energy

C) stopping energy

D) potential energy

10. For which position above does the ball on the end of the string have the greatest gravitational potential energy?

A) PE = m g h

The height is greatest at position A.

11. For which position above does the ball on the end of the string have the greatest kinetic energy?

D) KE = (¹/₂) m v²

E_Tot = PE + KE

KE = maximum when PE = minimum

PE = minimum at D

Therefore, KE = maximum at D

12. Which requires more work: lifting a 5 kg sack vertically 2 meters or lifting a 10 kg sack vertically 4 meters?

A) lifting the 5 kg sack

B) both require the same amount of work

C) lifting the 10 kg sack

W = m g h

W₅ = (5 kg) ( 10 m/s²) ( 2 m) = 100 J

W₁₀ = (10 kg) (10 m/s²) (4 m) = 400 J

D) both require the same amount of force

13. A 10 kg sack is lifted 2 meters in the same time as a 5 kg sack is lifted 4 meters. The power expended in raising the 10 kg sack compared to the power used to lift the 5 kg sack is

A) half as much

B) the same

P = W / t

P = m g h / t

P₅ = (10 kg) (10 m/s²) (2 m) / t = 200 J / t

P₁₀ = (5 kg) (10 m/s²) (4 m) / t = 200 J / t

C) twice as much

D) four times as much

14. A 2 kg mass is held 4 m above the ground. What is the approximate potential energy of the mass with respect to the ground?

A) 8 J

B) 40 J

C) 80 J

PE = m g h

PE = (2 kg) (10 m/s²) (4 m)

PE = 80 J

D) 160 J

15. A 2 kg mass has 40 J of potential energy with respect to the ground. Approximately how far is it located above the ground?

A) 1 m

B) 2 m

PE = m g h

PE = (2 kg) (10 m/s²) (2 m)

PE = 40 J

C) 3 m

D) 4 m

16. Using 1,000 J of work, a model elevator is raised from the ground floor to the second floor in 20 seconds. How much power does the elevator use?

A) 50 W

P = W / t

P = 1,000 J / 20 s

P = 50 J / s

P = 50 W

B) 500 W

C) 2 kW

D) 20 kW

17. A car moves 4 times as fast as another identical car. Compared to the slower car, the faster car has

A) the same kinetic energy

B) 4 times the kinetic energy

C) 8 times the kinetic energy

D) 16 times the kinetic energy

KE = (¹/₂) m v²

If v is 4 times greater then v² is 4² = 16 times greater.

18. A car moving at 50 km/hr skids 20 m with locked brakes. How far will the car skid with locked brakes if it is traveling at 150 km/hr?

A) 40 m

B) 60 m

C) 90 m

D) 180 m

W = F s = KE

Increasing the speed by a factor of three means KE has increased by a factor of nine.

The brakes only exert so much force as they skid; the force is constant.

The stopping distance must increase by a factor of nine.

This was also a homework problem, Pb 6.1 .

19. When a rifle is fired it recoils so both the bullet and rifle are set in motion. The rifle and bullet ideally acquire equal but opposite amounts of

A) kinetic energy

B) momentum

Momentum is always conserved

C) potential energy

D) all of the above

20. What does an object have when moving that it doesn`t have when at rest?

A) momentum

At rest, an object's momentum must be zero.

But an object can have potential energy while it is at rest.

And an object certainly has mass while it is at rest.

B) energy

C) mass

D) all of the above

21. If an object has kinetic energy, then it also must have

A) momentum

B) velocity

C) speed

D) all of the above

If it has KE, it has velocity and that means it also has momentum and speed.

| Back to 3050's Home Page | Back to Calendar | ToC, Ch 7 | Ch 8, Rotation |