Velocity Vectors

Velocity is a vector. That means velocities add just like force vectors. All vectors behave the same way. Once you know how to add forces, you also know how to add velocities -- and all other vectors.

Consider an airplane that flies at 80 km/h, due North, or North relative to the air. That is, the airplane heads North relative to the air. But the air is blowing at 60 km/h, due East relative to Earth. What is the airplane's velocity relative to Earth? That is, how fast is the airplane going, and in which direction, as we watch from the Earth? We can add these velocities together with a vector addition diagram like this.

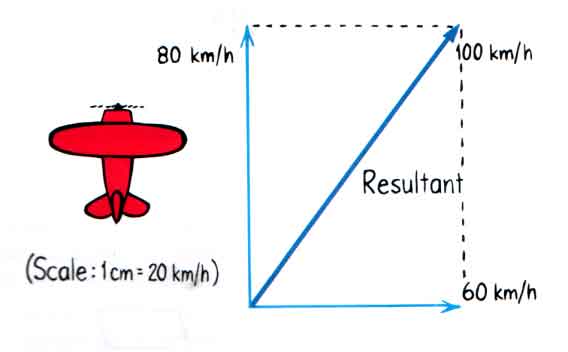
It might be easier to see if we thought about the wind first and drew in the velocity of the air relative to Earth by first drawing the 60 km/h velocity vector pointing to the East. Then, at the end of that vector, we start the new velocity vector, the velocity of the airplane relative to the air, the 80 km/h velocity vector pointing North. That velocity addition diagram looks like this diagram below. The resultant -- the velocity of the airplane relative to Earth -- is the vector that starts where we started and ends where we ended. That, too, is shown below.

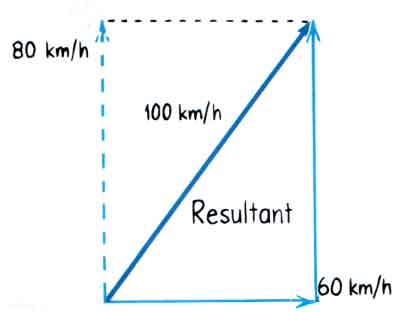
Or we might start with the velocity vector of the airplane's velocity relative to the air, the 80 km/h velocity vector pointing North. Then, at the end of that vector, we start the next vector, the velocity of the wind relative to Earth, the 60 km/h velocity vector pointing East. That velocity addition diagram looks like this diagram below. The resultant -- the velocity of the airplane relative to Earth -- is the vector that starts where we started and ends where we ended. That, too, is shown below.

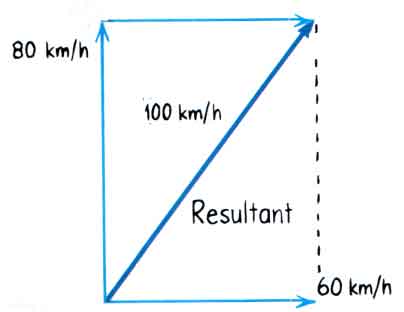
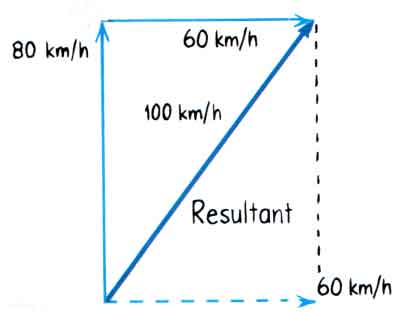
In either case, the resultant is the same. Using the same scale we used to construct the 60 km/h and 80 km/h velocity vectors on the diagram, we measure the length of the resultant. We will find that the resultant corresponds to a velocity of 100 km/h. The resultant velocity of the airplane relative to Earth is 100 km/h.

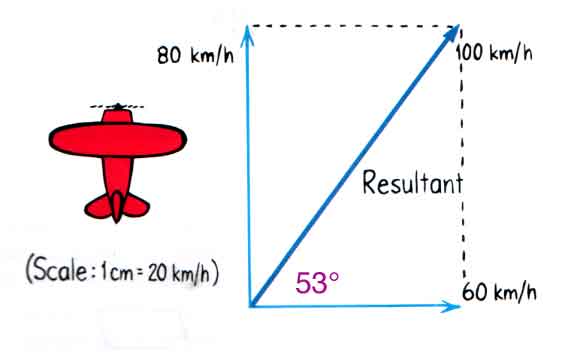
But we are not entirely done. Velocity is a vector! That means we need a direction for this resultant velocity. Again, we pull out a protractor and measure the angle that gives the direction of this resultant. Measured counterclockwise from the horizontal direction in our diagram, this angle is 53^o as shown above. That is a perfectly good way to describe the resultant velocity. The airplane flies at 100 km/h at an angle of 53^o counterclockwise from East.

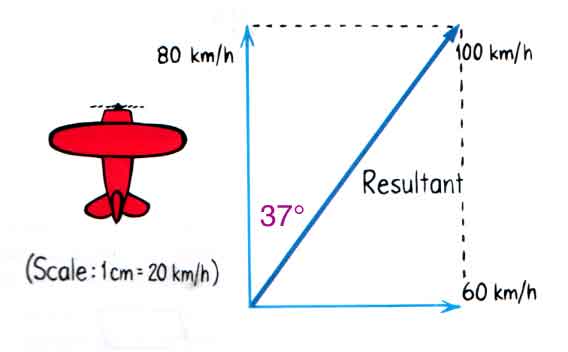
However, a pilot would probably describe this a little differently. Pilots usually give directions measured from North. So a pilot might describe this by saying the airplane flies at 100 km/h at an angle of 37^o East of North. That is shown in the diagram below. That is also a perfectly good way to describe the resultant velocity. The two phrases are equivalent.