

Force Vectors
Recall the ancient joke about moving a piano through a doorway.
The point of this ancient joke is simply to remind you that the direction of a force is important.
Force is a vector!
How can we add two forces?
Force diagrams -- or vector diagrams -- provide a good, easy, and quite visual way to add forces.
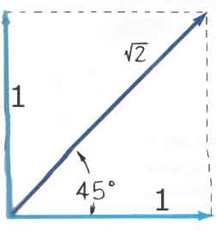
Consider a force of 1 N upward and a force of 1 N to the right. What is the sum of these forces? To emphasis that we are dealing with vectors, we might ask for the vector sum of these forces. When we ask this, we are asking what single force -- its magnitude and direction -- has the same effect as these two vectors. We might also call this sum of the forces the resultant force or the resultant vector. This vector sum of the two forces provides the same resultant.We will represent each force, or each vector, by an arrow in our drawing or diagram.

Make the drawing carefully (of course!). Now just measure the length of the resultant and measure the direction (using a protractor).
Consider a force of 30 N acting up and a force of 40 N acting to the right.
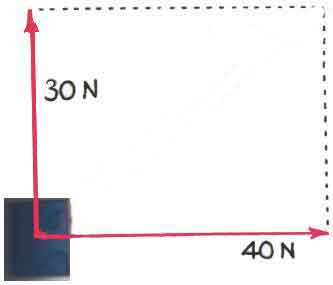
What is the vector sum of these two forces? Or, what is the resultant of these two forces? We begin my making a careful diagram with some scale chosen so that one centimeter represents, perhaps, 10 N. In that case, the upward arrow in the diagram would be 3 cm long and the right arrow in the diagram would be 4 cm long. The resultant -- the vector sum -- of these two vectors is the diagonal of the rectangle (or parallelogram) they form. We would measure this arrow to be 5 cm long on our diagram; that means the magnitude of the resultant is 50 N (remember, 1 cm represents 10 N of force).
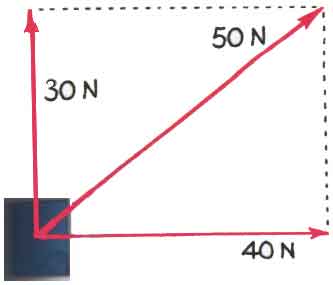
It will often help to move the forces around as we make these vector addition diagrams. We could start with the force of 40 N to the right. At the end of that vector, we could start the 30 N force pointing upward. Then the resultant is the force -- or arrow or vector -- that starts where our diagram started and ends where our diagram ended. That would look something like this,
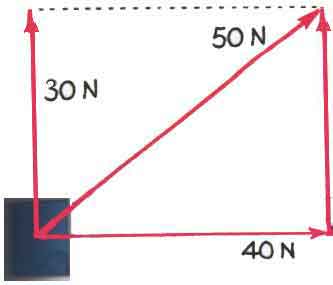
Or, wcould start with the force of 30 N pointing up. At the end of that vector, we could start the 40 N force pointing to the right. Then the resultant is the force -- or arrow or vector -- that starts where our diagram started and ends where our diagram ended. That would look something like this,
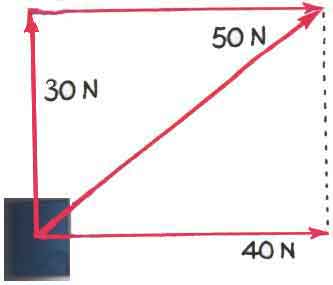
In either case, the resultant is the same.The order we do the vector addition does not matter. This is the same as ordinary addition,
4 + 3 = 3 + 4
If you want to add a word to your vocabulary, we can say that both vector addition and regular addition are commutative!
What about the direction? Again, we can pull out a protractor and measure the angle or the direction of this resultant force. We would find that it is directed at an angle of 37o above the horizontal as shown in the diagram here.
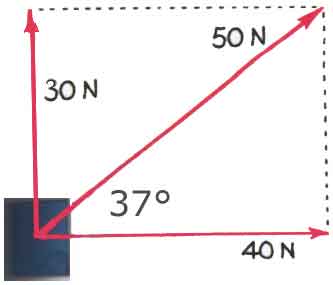
|
|
|||