

Homework
Ch 4; Newton's Second Law
Ex 2, 3, 5, 6, 9, 11, 17, 18, 19, 29, 32, 35, 42, 42; Pb 4, 5, 7
![]()
Ex 4.* Before the time of Galileo and Newton, it was thought by many learned scholars that a stone dropped from the top of a tall mast of a moving ship would fall vertically and hit the deck behind the mast by a distance equal to how far the ship had moved forward while the stone was falling. In light of your understanding of Newton's Laws, what do you think about this?
As we have seen on The Mechanical Video, and as I have tried to demonstrate in walking back and forth in front of the classroom while throwing a ball, the ball or stone should fall and hit the deck at the base of the mast.
Ex 4.2 Can the velocity of an object reverse direction while mintaining a constant acceleration? If so, give an example; if not, explain why.
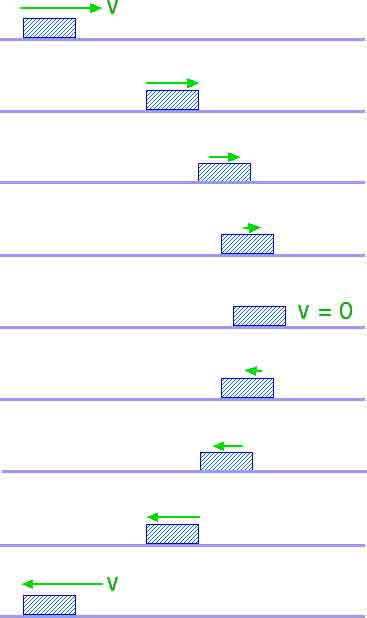
Yes, as shown in the sketch here. Consider a block moving to the right with an acceleration to the left as shown here. The block will eventually come to rest with v = 0. If the acceleration stays the same, the block will now move to the left and continue to increase its speed. Throughout the sketch shown here, the acceleration is constant and to the left.
Ex 4.3 If an object is not accelerating, can you conclude that no force acts on it?
You can conclude that there is no net force on the object. There may be many separate forces acting on it, but their sum is zero!
Ex 4.5 If it takes 1 N to push horizontally on your book to make it slide at constant velocity, how much force of friction acts on the book?
Horizontally, your 1 N force acts to the right while the friction force acts to the left. If the book slides at constant velocity that means it moves with zero acceleration so the net forcemust be zero. Therefore, the friction force is also 1 N.
Ex 4.6 Is it possible to go around a curve in the absence of a force?
No, going around a curve means the velocity changes direction. Any change in velocity requires an acceleration. And any acceleration requires a (net) force.
Think of what happens during the winter when there may be ice on a curve so that the force of friction between tires and road is very small. Then cars can not go around such a curve and end up in a ditch.
Ex 4.9 A 400-kg bear grasping a vertical tree slides down an constant
velocity. What is the friction force that acts on the bear?
The bear whose mass is 400 kg has a downward
weight of 4,000 N since
W = m g = (400 kg)(10 m/s2) = 4,000 N
Since the bear slides down at constant velocity (or zero acceleration!), the net force on the bear must be zero. The net force is the sum of the downward weight and the upward friction force. These two must add to zero. So the friction force is also 4,000N.
Ex 4.11 In the orbiting space shuttle you are handed two identical boxes, one filled with sand and the other filled with feathers. How can you tell which is which without opening the boxes?
Shake the boxes back and forth or up and down and see which is easier to accelerate.
Ex 4.17 What happens to your weight when your mass increases?
Since weight is proportional to mass, or W = m g, any increase in mass corresponds to a proportional increase in weight.
Ex 4.18 What is your own mass in kilograms? Your weight in newtons?
Recall that the a mass of 1 kg has a weight of 2.2 lbs. To find mass in kilograms, take your weight in lbs and divide by 2.2 (this means a weight of 2.2 lbs corresponds to a mass of 1.0 kg or a weight of 22 lbs corresponds to a mass of 10 kg or a weight of 220 lbs corresponds to a mass of 100 kg.)
Recall that the weight of 1 kg is 9.8 newtons. To find your weight in newtons, take your mass in kilograms and multiply by 9.8 .
Here is a short table:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ex 4.19 A rocket becomes progressively easier to accelerate as it travels through space. Why is this so?
The force of the rocket enging -- called the thrust -- remains constant. But the mass of the rocket decreases as it uses its fuel. As this constant forces continues to act on a smaller and smaller mass, the acceleration increases.
Ex 4.29 When you jump vertically off the ground, what is your acceleration after you reach your highest point?
Once your feet leave the ground, you're in free fall. Once your feet leave the ground, the only force acting on you is the force of gravity, your weight. Once your feet leave the ground, your acceleration is the acceleration of gravity, downward at 9.8 m/s2.
Ex 4.32 A friend says that as long as a car is at rest,
no forces act on it. What do you say if you're in the mood to correct this
statement?
For a car -- or any object -- at rest, the net force is zero.
But having the net force to be zero is not the same things
as having no forces acting on the car at all!
Ex 4.35 What is the net force on a 1 N apple when you hold it at rest above your head? What is the net force on it after you release it?
If you're holding the apple at rest, the net force on the apple is zero.
Once you drop the apple, the only force on it is its weight of 1 N
Ex 4.43 How does the terminal speed of a parachutist before opening a parachute compare to terminal speed after? Why is there a difference?
Ex 4.44 How does the gravitational force on a falling body compare with the air resistance it encounters before it reaches terminal velocity? After?
Ex 4. 31 What is the net force on an apple that weighs 1 N when you hold it at rest above the floor? What is the net force on it when you release it?
For anything at rest, the net force is zero.

When you release the apple, the only force on it is the force of gravity, which we call the weight of the apple, and we are told that that is one Newton.

Ex 4.44 How does the weight of a falling body compare to the air resistance it encounters just before it reaches terminal velocity? After?
Before reaching terminal velocity, the falling body is still accelerating, so its weight (the force of gravity) is still greater than the force due to air resistance.
After reaching terminal velocity, the falling body falls with constant speed so the net force on it must be zero. This means the force of gravity (its weight) acting downward is just balanced by the force of air resistance acting upward.
![]()
Pb 4.4 If a mass of 1 kg is accelerated 1 m/s2 by a force of 1 N, what would be the acceleration of 2 kg acted on by a force of 2 N?
Use Newton's Second Law,
2 = 2 x ?
2 = 2 x a
a = 1
a = 1 m/s2
Pb 4.5 How much acceleration does a 747 jumbo jet of mass 30 000 kg experience in takeoff when the thrust of each of four engines is 30 000 N (for a total thrust of 120 000 N)?
Again, use Newton's Second Law,
120 000 = (30 000) a
a = 4
a = 4 m/s2
Pb 4.7 A firefighter of mass 80 kg slides down a vertical pole with an acceleration of 4 m/s2. What frictional force does the pole exert on her?
First, we can find the net force, for that is always the F that appears in Newton's Second Law,
Fnet = (80 kg) (4 m/s2)
Fnet = 320 N
What forces make up this net force Fnet? Gravity pulls down with the firefighter's weight,
w = (80 kg) (10 m/sw)
w = 800 N
Then there is the force of friction, Ff, which opposes the firefighter's motion. So the force of friction Ff must point up. The net force Fnet is made up of these two forces,
320 N = 800 N - Ff
320 N = 800 N - 480 N
Ff = 480 N
![]()
Typical multiple-guess questions:
1. Mass is a measure of
a) the volume of an objectb) the size of an object
c) how difficult it is to change the motion of an object
d) the velocity of an object
2. The weight of an object is
a) the same thing as the mass of an objectb) the sum of all the forces on an object
c) the force of gravity on an object
d) always less than the mass, even in a vacuum
3. The net force on a 1-kg object, at rest, is
a) 9.8 Nb) 4.9 N
c) 1.00 N
d) zero
4. The net force on a 1-kg object, in free fallt, is
a) 9.8 Nb) 4.9 N
c) 1.00 N
d) zero
5. A force of 24 N acts on an object whose mass is 6 kg. This causes the object to accelerate at
a) 2 m/s2b) 4 m/s2
c) 6 m/s2
d) 10 m/s2
6. A car, with mass of 1,000 kg, accelerates at 2 m/s2. The net force exerted on the car must be
a) 500 Nb) 1,000 N
c) 2,000 N
d) 10,000 N
7. The weight of a 1,000-kg car is
a) 500 Nb) 1,000 N
c) 2,000 N
d) 10,000 N
8. A fireman, whose weight is 500 N, slides down a pole with an acceleration of 3 m/s2. The forces that act on him are his weight pulling him down and the force of friction pulling up on him to slow him down. The force of friction must be
a) 90 Nb) 150 N
c) 350 N
d) 500 N
Answers to typical multiple-guess questions:
1. Mass is a measure of
a) the volume of an objectb) the size of an object
c) how difficult it is to change the motion of an object
d) the velocity of an object
2. The weight of an object is
a) the same thing as the mass of an objectb) the sum of all the forces on an object
c) the force of gravity on an object
d) always less than the mass, even in a vacuum
3. The net force on a 1-kg object, at rest, is
a) 9.8 Nb) 4.9 N
c) 1.00 N
d) zero
4. The net force on a 1-kg object, in free fallt, is
a) 9.8 Nb) 4.9 N
c) 1.00 N
d) zero
5. A force of 24 N acts on an object whose mass is 6 kg. This causes the object to accelerate at
a) 2 m/s2b) 4 m/s2
c) 6 m/s2
d) 10 m/s2
F = m a 24 N = ( 6 kg ) ( a )
24 N = ( 6 kg ) ( 4 m/s2)
a = 4 m/s2
6. A car, with mass of 1,000 kg, accelerates at 2 m/s2. The net force exerted on the car must be
a) 500 Nb) 1,000 N
c) 2,000 N
d) 10,000 N
7. The weight of a 1,000-kg car is
a) 500 Nb) 1,000 N
c) 2,000 N
d) 10,000 N
w = mg w = (1,000 kg) (10 m/s2)
w = 10,000 N
8. A fireman, whose weight is 500 N, slides down a pole with an acceleration of 3 m/s2. The forces that act on him are his weight pulling him down and the force of friction pulling up on him to slow him down. The force of friction must be
a) 90 Nb) 150 N
c) 350 N
d) 500 N
F = ma Fnet = ma
Fnet = Fgravity - Ffrict
Fgravity = w = m g
500 N = m (10 m/s2)
m = 50 kg
Fnet = ma = (50 kg) (3 m/s2)
Fnet = 150 (kg m/s2)
Fnet = 150 N
Fnet = Fgravity - Ffrict
150 N = 500 N - Ffrict
Ffrict = 500 N - 150 N = 350 N
Ffrict = 350 N
![]()
|
|
|||