As sketched in Figure 20.3, Young first passed light through a slit. Light continued from this slit, spreading out as if it had originated from a tiny source. This light proceeded through a set of two slits and then continued on to fall on a distant screen where it could be viewed. Imagine shooting ping-pong balls through such a maze. They would either be stopped entirely or would fall on the distant screen in two places only. But Young observed an entirely different pattern for light. The light on the screen formed a complex pattern of alternating dark and bright bands that could not be explained by a beam of particles. This interference pattern can be explained only by assuming that light is a wave. This experiment marked a major turning point in understanding the nature of light. Physics is an experimental science and theories are accepted because they agree with experiments and theories are rejected because they disagree with experiments. Young's double slit experiment established the wave nature of light.

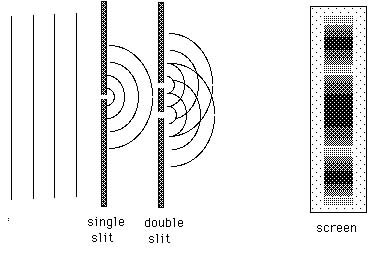
But first we must pause and explain the importance of having a single slit in front of the two slits. This single slit is necessary to provide coherent light to the two slits. Light from the filament of a bulb or from the surface of the Sun comes from an enormous number of atoms. These atoms emit their contribution to the total light in a random or incoherent manner. This usual, incoherent light may be compared to a group of students walking down a sidewalk between classes; there is no particular order or repeatability or predictability to their footsteps. Coherent light may be compared to a marching band at half time; there is a definite relationship in their footsteps. This coherence of the light is necessary to see interference effects. Today a more common source of coherent light is a laser. If laser light is used, it may be shone directly onto the double slits as sketched in Figure 20.4. The coherence and brightness of laser light make it much easier to observe this double slit interference pattern.

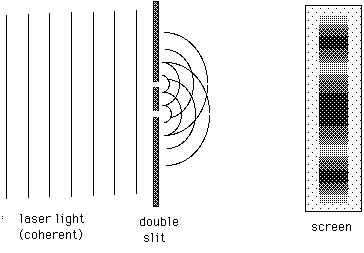
This double-slit interference pattern of alternating dark and bright bands or fringes comes about because light arriving at various positions has traveled different distances from the two slits to the screen. If the two light waves arrive in phase-both trying to produce a crest or both trying to produce a valley-constructive interference occurs and a bright region is seen. If the two light waves arrive out of phase-one trying to produce a crest and the other trying to produce a valley-destructive interference occurs and a dark region is produced.

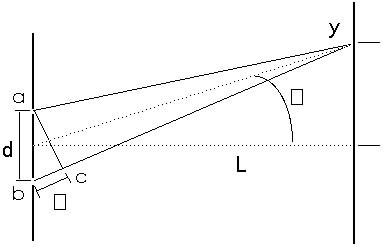
Figure 20.5 is a somewhat distorted sketch showing the path taken by light as it travels from the two slits to some position labeled y on a distant screen. The distance d between the two slits is greatly exaggerated so we can see what is happening. Because the light is coherent when it reaches the slits, the light leaves the two slits in phase or doing the same thing-either waving up or down, but looking exactly the same-as it leaves both slits. Light leaves the two slits at positions a and b and travels to y. The distance from a to y is the same as the distance from c to y. Light from slit b travels the distance from b to c farther; this extra distance is labeled as .

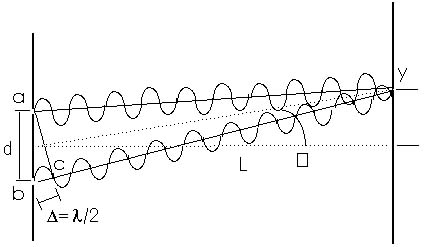
In Figure 20.6, this extra distance traveled by the light from one slit compared to light from the other slit is one-half a wavelength. For convenience, we can write this as

= /2 (dark)

where the Greek letter (lambda) is used to stand for one wavelength. From point c to position y the light travels the same distance-the same number of wavelength-as the light from slit a. Since the extra distance from b to c is one-half a wavelength, the light from the two slits arrives at position y "out of phase". When light from one slit is "up" or positive, light from the other slit is "down" or negative. The two light waves interfere destructively and the region at y is dark. The light waves from the two slits cancel each other.

If the extra distance is one and one-half wavelengths or two and one-half wavelengths-or any integer plus one-half wavelength-the light waves will also arrive at the screen out of phase and destructive interference will occur and a dark region will be produced. We can write this as

= (m + 1/2) (dark)

for destructive interference or dark regions, where m is an integer or a whole number (m = 0, 1, 2, 3, ...).

In Figure 20.7, the extra distance traveled by the light from one slit to the screen compared to light from the other slit to the screen is one whole wavelength. Again, for convenience, we can write this as

= (bright)

where, again, means one wavelength. From point c to position y the light travels the same distance-the same number of wavelengths-as the light from slit a to position y. Since the extra distance from b to c is a full wavelength, the light from the two slits arrives at position y "in phase". When light from one slit is "up" or positive, light from the other slit is also "up" or positive. When light from one slit is "down" or negative, light from the other slit is also "down" or negative. The two light waves interfere constructively and the region at y is bright. The light waves from the two slits reinforce each other.

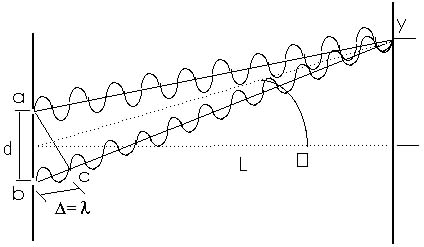
If the extra distance is two full wavelengths or three full wavelengths-or any integer times the wavelength-the light waves will also arrive at the screen in phase and constructive interference will occur and a bright region will be produced. We can write this as

= m (bright)

for constructive interference or bright regions, where m is an integer or a whole number (m = 0, 1, 2, 3, ...).

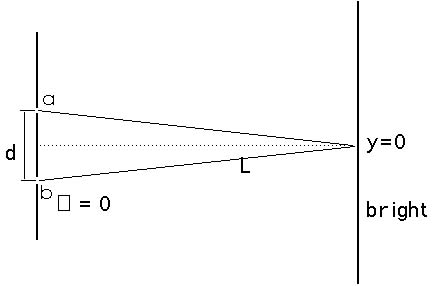
Figure 20.8 shows light waves originating at the slits a and b and arriving at the center of the diffraction pattern on a distant screen. From the symmetry involved, you can see that the paths taken by the light waves from the two slits must be identical. This means that is zero and the two waves arrive at the screen in phase. That is, they interfere constructively and we will see a bright area or a bright region or a bright fringe at the center of the double slit diffraction pattern. This is an example of constructive interference for = m with m = 0 but since this is at the center of the pattern, it is worthwhile to point this out in particular.