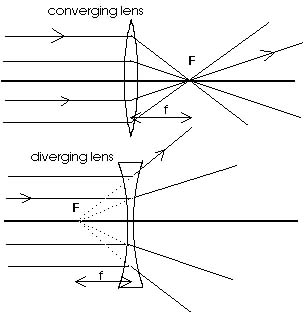
Light is bent at both surfaces of a lens. We will restrict our attention to thin lenses; lenses whose thickness is much smaller than any other dimension of interest in the problem. Then we may pretend the light undergoes a single refraction at the position of the lens. Rays of light parallel to the optic axis, as in Figure 18.15, strike a converging lens and are bent or refracted; these rays converge on a single, common point. By symmetry this point must lie on the optic axis. It is called the focal point and is labeled with a capital F. The distance between the focal point and the lens is called the focal length and is labeled with a lower case f; the focal length is positive for a converging lens (f > 0). These same rays of light parallel to the optic axis, as in Figure 18.15 again, strike a diverging lens and are bent or refracted so they appear to diverge from a single, common point. By symmetry this point must lie on the optic axis. It is called the focal point and is labeled with a capital F. The distance between the focal point and the lens is called the focal length and is labeled with a lower case f; it is negative for a diverging lens (f < 0). This should appear very similar to our earlier discussion of concave and convex mirrors. There is one difference. A lens can be turned around so there is really a focal point on both sides of a lens with the same value of f on either side.

Q: What kind of mirror corresponds to a converging lens?

A: A concave mirror is quite similar to a converging lens.

Q: What kind of mirror corresponds to a diverging lens?

A: A convex mirror is quite similar to a diverging lens.