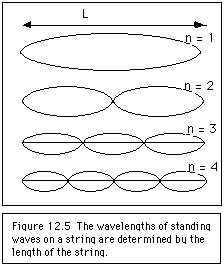
In the previous chapter we talked of standing waves on a string; this was an example of resonance. As a reminder, look at Figure 12.5 which again shows standing waves on a string. The positions that do not move are called nodes and the positions of maximum amplitude are called antinodes. Since the ends are fixed, the ends are nodes. Each "loop" of the standing wave-the portion from node to node-is one half a wavelength. To fit standing waves onto a string we must have

n (half a wavelength) = L

where n is an integer ( n = 1, 2, 3, …) and L is the length of the string. Figure 12.5 shows the standing waves that may be present for n = 1, n = 2, n = 3, and n = 4. Only waves with certain, particular wavelengths show up as standing waves on a string.

In the previous chapter we also found the following direct connection between wavelength and frequency,

(frequency) (wavelength) = wavespeed

Thus, our restriction that standing waves on a string have only certain, particular wavelengths means that standing waves on a string have only certain, particular frequencies. There are similar restrictions for standing waves in a pipe-as in an organ pipe or a clarinet, trumpet, or saxophone.

The lowest of these frequencies is for n = 1 and has the longest wavelength; this is called the fundamental frequency. Higher frequencies are called harmonics. The frequency for n = 2 is called the second harmonic, while the frequency for n = 3 is called the third harmonic, and so on. These harmonics are also sometimes called overtones. With great care you may be able to excite just a single harmonic as a standing wave on a string. Usually, however, if you pluck or bow a string you will cause it to vibrate as a combination or superposition of many of these frequencies.

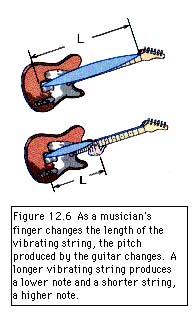
The pitch of a sound-how low or how high it is-is determined by the fundamental frequency-the lowest frequency of the standing waves that are produced. For stringed instruments, the length of the string itself is changed to alter the pitch. For violins and guitars and banjos, the position of the musician's fingers determines the length of the string available to vibrate; this is illustrated in Figure 12.6. A longer string means a longer wavelength for the standing wave and a lower pitch. For a piano, different strings are struck with a hammer-again, shorter strings produce a higher pitch while longer string produce a lower pitch.

A pipe organ uses long pipes to produce notes with low pitch and long wavelengths and short pipes for notes of high pitch and short wavelengths as illustrated in Figure 12.7. You can hear this effect yourself by blowing across several pop bottles filled with different amounts of water. The frequency (or pitch) of the sound produced is determined by the standing waves set up in the column of air. Long columns of air produce low frequencies and short columns of air produce high frequencies.

A slide trombone is fun to watch for the length of the resonating tube of air can be varied continuously. Most wind instruments-like saxophones, clarinets, and oboes-produce different notes by opening and closing holes in a tube so that standing waves of different wavelengths are produced. The bass drone on a set of great highland bagpipes produces a note one octave lower than the tenor drones; therefore, it is essentially twice as long as the tenor drones. Figure 12.8 shows a few examples of how the pitch of a note played by an instrument is determined.

Figure 12.9 shows the range of frequencies that can be produced by a piano and by the stringed instruments of the violin family-violin, viola, cello, and stringed bass. Notice, once again, that lower frequencies come from longer, heavier strings and higher frequencies are produced by shorter, lighter strings. This is true for the piano as well as for the violin family of instruments.