If we wiggle one end of the rope at different frequencies, we will find there are only certain, particular frequencies that give much of a pattern or provide waves with large amplitude. We will find large amplitudes only for the situations sketched in Figure 11.14. Each of these patterns is called a standing wave for the wave does not move along the rope in these cases. We can fit one "loop" or two loops or three loops or any whole number of loops between the ends of our rope. Each of these loops is one half a wavelength. The areas between the loops-where the rope does not move at all-are called "nodes" and the areas of maximum amplitude-where the rope moves the most-are called "antinodes". This is shown in Figure 11.15. When a guitar string is plucked or a violin string is bowed or a piano string is struck, standing waves are produced. This restricts the wavelengths-or the frequencies-that may be produced and gives an instrument its characteristic sound or voice. The same will be true of organ pipes or other musical instruments.

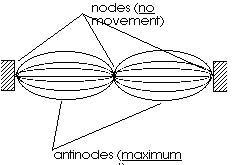
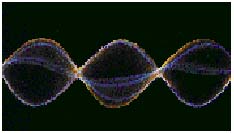
For standing waves on a string-like standing waves on a rope in a Physics demonstration or standing waves on a guitar string when it is plucked or standing waves on a violin string when it is bowed-this restriction is that a whole number of "loops" fit on the length of the string. Each loop is one-half a wavelength. That means that the a whole number times half a wavelength must equal the length of the string. We can write that as: