If you strike the rope repeatedly or wiggle the end of it up and down again and again, you will cause a continuous series of pulses to move along the rope. Such a continuous string of disturbances traveling down the rope is known as a wave. Most of the time the cause of the wave will be something that moves back and forth with simple harmonic motion. This causes a wave that looks like a sine curve from trigonometry so these waves are called sine waves or sinusoidal waves.

Energy is transferred from one place to another by a wave but no matter is transferred. We even sing of "amber waves of grain" and we can see waves move along a wheat field. Each head of grain remains attached to its stalk which is attached to the ground. Yet the wave-or the disturbance-moves across the field from one place to another.

Figure 11.2 shows a wave with several of its characteristics labeled. The tops of the waves are often referred to as crests and the bottoms of the waves, as valleys. The distance between waves is usually easier to measure as the distance between crests or the distance between valleys; this is known as the wavelength. In the figure a dotted line shows where the medium (like a stretched rope) would be if it were not for the wave going by; this is the equilibrium position of the medium. The maximum distance moved away from this equilibrium position is the amplitude. The wave moves with a wave speed v as indicated in the figure.

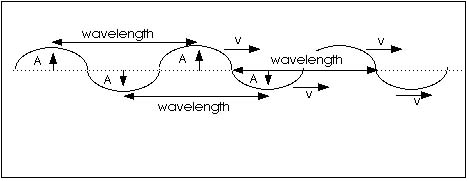
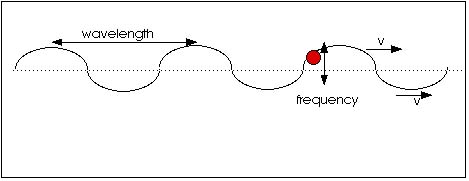
Figure 11.3 shows a fishing bobber that moves up and down as water waves go by. Notice that the bobber only moves up and down; it is not carried along by the water wave. The bobber moves up and down in simple harmonic motion with some frequency as the waves come by with some wavelength. If the frequency of the wave is, say, 3 Hz (3 oscillations per second) and the wavelength-or distance from one wave to another-is 4 cm, what is the wave speed v? Each time the bobber moves up and down, the wave has moved 4 cm and it moves up and down 3 times a second so the speed of the wave must be 12 cm/s. We can generalize this and state that the wave speed is the product of the frequency and the wavelength,

wave speed = (frequency) (wavelength)

Q: What is the wave speed if a wave has a frequency of 6 Hz and a wavelength of 15 cm?

A: wave speed = (frequency) (wavelength)

v = (6 Hz) (15 cm)

v = 90 cm/s

Q: Can the wavelength be measured any way other than from crest to crest or from valley to valley?

A: Yes, measuring from crest to crest or from valley to valley is usually easiest to visualize and easiest to actually do. But the distance from any point on one wave to the corresponding point on the next wave would provide the same wavelength.