|
|

|
|

The resulting torque is proportional to the angle through which the support has been twisted. This proportional restoring force-or restoring torque in this case-is just what we need to have simple harmonic motion.
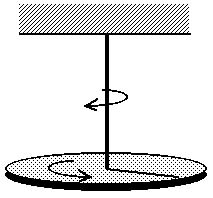
cause it to exert a restoring torque or "rotational
force". If the fiber or support is attached to an
object that can rotate back and forth, this can
make a torsional pendulum.
As the disk rotates back toward its equilibrium position, it gains
kinetic energy and overshoots its equilibrium position. It continues
with the support now trying to rotate it back, in the opposite
direction. This motion continues and is simple harmonic motion.
The period of the motion depends upon the stiffness or strength
of the support and upon the moment of inertia of the disk or whatever
object is rotating.
Leave the figure on for this paragraph.
The fact that such a system is a simple harmonic oscillator is
important for time-keeping. Being a simple harmonic oscillator
means the period is constant. The balance wheel in mechanical
watches or clocks is such an arrangement of a rotating wheel attached
to a support. In these cases, the support is often in the form
of a spring. This is the rotational equivalent of a mass and a
spring. Such an arrangement is called a torsional pendulum.
Leave the photo or video on for this paragraph.

|
|