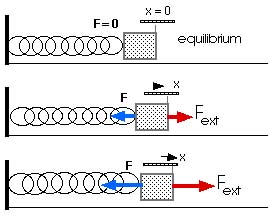
This same idea can be shown on a graph. The graph of force and stretch of the spring is a straight line. The slope of this line is k, the "spring constant", which describes how strong or weak the spring is. The spring constant k is large for a strong spring and k is small for a weak spring.

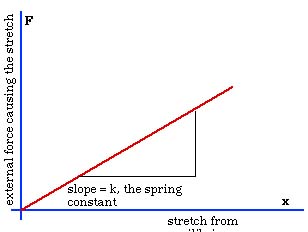
Figure 10.8 A graph of the stretch of a spring and the external force causing the stretch is a straight line. The slope of the line is the spring constant, k.

Since a mass attached to a spring is a simple harmonic oscillator, we know the amplitude does not affect the period. If the mass is moved only a little from equilibrium and released, it will oscillate back and forth gently with some period. If we pull the mass a larger distance from equilibrium and release it, it will move back and forth with more speed but the period will remain the same. If we now pull it an even greater distance from equilibrium and release it, it will rush back and forth with greater speed but the period will still be the same.

This is a characteristic of all simple harmonic oscillators.

What, then, does determine the period? You know-both from your own practical experience and from Newton's second law-that a larger mass will be more difficult to move. The period will increase as the mass increases.

More mass-with the same spring-will mean a larger period.

What else determines the period? How strong or weak the spring is will certainly affect the motion. A stronger spring-with a larger value of k-will move the same mass more quickly for a smaller period. As the spring constant k increases, the period decreases.

These two ideas are contained in the equation

which gives the period T for a mass m attached to a spring with spring constant k.

Q: Thinking in terms of Newton's second law, why would a greater mass lead to a longer period?

A: Newton's second law, F = ma or a = F/m , tells us that a larger mass will have a smaller acceleration (for the same force) so that a greater mass will simply move slower and, therefore, take a longer time to complete its motion.

Q: Thinking in terms of Newton's second law, why would a stiffer spring lead to a shorter period?

A: A stiffer or stronger spring means a greater force in Newton's second law, F = ma. For a given mass, that means a greater acceleration so the mass will move faster and, therefore, complete its motion quicker or in a shorter period.