PHY 1361
First Hour Exam

February 7, 2001

Statistics:

High: 98%

Mean: 75%

Low: 55%

| Return to PHY 1361 Calendar |

Pace yourself! Do not spend too much time on any one particular problem or question. There are four calculational problems and four short-essay, quickie discussion questions.

Read through the entire exam first. If you find one of the questions or problems is taking too long, leave it and go on to others. You can come back to that problem later if you have time.

Problem 3 is clearly the longest and most involved; allot a little more time for Problem 3.

Entropy is important. In picking and choosing topics for questions, I did not choose an entropy question for this hour exam. I expect ideas of entropy to reappear on the final exam.


1. (19.10) The concrete sections of a certain superhighway are designed to have a length of 25.0 m. The sections are poured and cured at 10.0oC. What minimum spacing should the engineer leave between the sections to eliminate buckling if the concrete is to reach a temperature of 50.0oC?

How much will the 25.0 m section expand as the temperature changes from 10.0oC to 50.0oC?

For concrete, the coefficient of thermal expansion is

12 x 10 - 6 (Co) - 1 (from Table 19.2, on p 588)
a = 12 x 10 - 6 (Co) - 1

The temperature change, T, is 40 Co; T = 40 Co

Now we can put all the pieces together and evaluate the expansion, L ;

L = [12 x 10 - 6 (Co) - 1][25.0 m][40 Co] L = 0.012 m
L = 1.2 cm

Since each concrete section will expand by 1.2 cm, there must be 1.2 cm between each section so they do not run into each other and cause compressive stresses.

2. (similiar to 20.8) A calorimeter contains 500 mL of water at 30oC and 300 g of ice at 0oC.

If all the ice melts, determine the final temperature of the system.
If the final temperature is 0oC, determine how much ice melts.

Qwater + Qice = 0
Qwater = cw mw T
Qwater = (4186 J/kg-Co) (0.500 kg) (Tf - 30oC)
Qwater = 2093 Tf (J/Co) - 62,790 J

Now, how much heat is gained by the ice? Does all of the ice melt? We do not know. So we must make an assumption -- or a guess. We then have to see if our result is consistent with that assumption.

Assumption: All the ice melts and Tf > 0oC
Be sure to check for consistency with our final answer and this assumption.
This ice is initially at 0oC so heat that it gains immediatly starts to melt the ice.  Remember, mice = m2 = 300 g = 0.300 kg. m2 is the mass of the ice after it has melted and is water at 0oC.

Qice = Qmelt + Qraise
Qice = mice L + c m2 DT
Qice = (0.300 kg)(3.33 x 105 J/kg) +           
          + (4186 J/kg-Co) (0.300 kg) (Tf - 0oC)
Qice = (0.300)(3.33 x 105 J) + (4186 J/Co) (0.300 kg) Tf
Qice = 99,900 J + 1,256 Tf (J/Co)
Qwater + Qice = 0
[2,093 Tf (J/Co) &endash; 62,790 J] + [ 99,900 J + 1,256 Tf (J/Co))] = 0
(2,093 + 1,256) Tf (J/Co) + (&endash; 62,790 + 99,900) J= 0
3,349 Tf (J/Co) + 37,110 J= 0
3,349 Tf (J/Co) = &endash; 37,110 J
Tf = &endash; (37,110 / 3,349) oC
Tf = - 11.1oC

Is that "believeable" or "reasonable"? It is between the lowest and highest initial temperature so that means it is, at least, "possible". No, this is colder than the ice! Our assumption was wrong! We must make another assumption.
Assumption: Tf = 0 and only part of the ice melts. Now we must determine how much of the ice melts.

Qwater + Qice = 0
Qwater = cw mw DT
Qwater = (4186 J/kg-Co) (0.500 kg) (Tf - 30oC)
Qwater = (4186 J/kg-Co) (0.500 kg) (0oC - 30oC)
Qwater = - 62,790 J

This ice is initially at 0oC so heat that it gains immediatly starts to melt the ice.  Remember, this time when some of the ice melts it does not change its temperature since Tf = 0oC.  We are now looking for  Mmelt .

Qice = Qmelt
Qice = Mmelt L
Qice = (Mmelt)(3.33 x 105 J/kg)
Qwater + Qice = 0
- 62,790 J + (Mmelt)(3.33 x 105 J/kg) = 0
(Mmelt)(3.33 x 105 J/kg) = 62,790 J
Mmelt = [62,790 / 3.33 x 105 ] kg
Mmelt = 0.188 kg
Mmelt = 188 g

As always, ask if this is "believeable" or "reasonable" -- or consistent with our assumptions.  Yes, this is consistent with our assumption of only part of the ice melting.  This amount of ice that melts is, indeed, less than our total, initial amount of ice.  So this answer seems plausible.

3. (similar to 21.26) Four liters of a monatomic ideal gas confined to a cylinder are put through a closed cycle. The gas is initially at 1.0 atm and at 300 K.
First, its pressure is tripled under constant volume.
It then expands isothermally to its original pressure and
finally is compressed isobarically to its original volume.

(a) Draw a PV diagram of this cycle.
Here is a sketch:

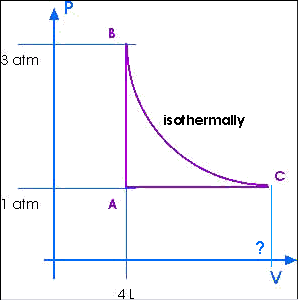
(b) What is the temperature of the isotherm?

P V = n R T
P V / T = constant
PA VA / TA = PB VB / TB
VB = VA
PA/TA = PB/TB
TB/PB = TA/PA
TB = (TA)(PB/PA)
TB = (300 K)(3 atm/1 atm)
TB = 900 K

(c) What is the volume at the end of this isothermal expansion?

P V = n R T
P V / T = constant
PC VC / TC = PA VA / TA
TC = TB = 3 TA
PC VC / TC = PA VA / TA
PC VC /3 = PA VA
PC VC = 3 PA VA
PC = PA
VC = 3 VA
VC = 3 (4 L)

VC = 12 L

(d) How much work is done in each process of this cycle?

WAB = 0
WBC = n R T ln[Vf/Vi]
WBC = n R T ln[VC/VB]
WBC = n R T ln[3]
WBC = n R (900 K) (1.10)
P V = n R T
n R = P V / T
n R = (12 atm) (1 L) / 900 K
n R = 0.0133 L-atm/K
WBC = (0.0133 L-atm/K) (900 K) (1.10)
WBC = 13.2 L-atm
WBC = 13.2 L-atm [0.001 m3/L][(1.013 x 105 N/m3)/atm]
WBC = 1,337 N-m
WBC = 1,337 J
WCA = P DV
WCA = (1 atm) (4 L - 12 L)
WCA = (1 atm) (- 8 L)
WCA = - 8 L-atm
WCA = - 8 L-atm [0.001 m3/L][(1.013 x 105 N/m3)/atm]
WCA = - 810.4 N-m
WCA = - 810 J

(e) What is the net work done during this cycle?

Wnet = WAB + WBC + WCA
Wnet = 0 + 1,337 J - 810 J
Wnet = 527 J

4. (22.7) An engine absorbs 1 600 J from a hot reservoir and expels 1 000 J to a cold reservoir in each cycle.
(a) What is the efficiency of the engine?

e = 1 - [Qc/Qh]

e = 1 - [ 1 000 J/1 600 J]
e = 1 - 0.625
e = 0.375
e = 37.5%

(b) What is the power output of the engine if each cycle lasts for 0.30 s?
For each cycle,

W = Qh - Qc
W = 1 600 J - 1 000 J
W = 600 J

Then the power is

P = W / t
P = 600 J / 0.30 s

P = 2 000 W = 2 kW

Conceptual Questions --

A. (19.Q14) Metal lids on glass jars can often be loosened by running them under hot water. How is this possible?

The coefficient of thermal expansion is much greater for metals than for glass. Heating a metal lid on a glass jar will cause the metal lid to expand far more than the glass. This should allow you to unscrew the metal lid from the glass jar.

 

B. (20 “Opener") Why can you get "burned" by biting into the hot CHEESE on a steaming pizza far easier than by biting into the CRUST of the pizza?

Cheese is primarily water with a large heat capacity while the crust has very little water and a very small heat capacity.


C. (Q21.2) One container is filled with helium gas and another with argon gas. If both containers are at the same temperature, which molecules have the higher rms speed?

At the same temperature, the average value of the translational kinetic energy [(1/2) m <v2>] will be the same for both helium and argon. Argon has a larger mass so it will have a smaller value of <v2> or vrms. Helium has a smaller mass so it will have a larger value of <v2> or vrms.


D. (Q22.3) Use the first law of thermodynamics to explain why the total energy of an isolated system is always constant.

The first law of thermodynamics is just a restatement of Energy Conservation. If a system is isolated no work is done on it and no heat is transferred to or from it. Energy may be transferred from one part of the system to another but the total energy remains constant.

 

| Return to PHY 1361 Calendar |

(C) 2001; Doug Davis; all rights reserved