

Magnetic Sources
Homework Solutions Questions 1, 2, 3, 4, 9, 18, 19
Problems 30.8A, 22, 23, 25, 32, 40, 60, 64
Q1 Is the magnetic field created by a current loop uniform?
Not at all; it varies with position -- it varies in direction and magnitude -- as shown in this sketch:
Q2 A current in a conductor produces a magnetic field that can be calculated using the Biot-Savart law. Since current is defined as the rate of flow of charge, what can you conclude about the magentic field produced by a stationary charge? What about moving charges?
The magnetic field produced by a stationary charge is zero. A moving charge is a current so it will produce a magnetic field.
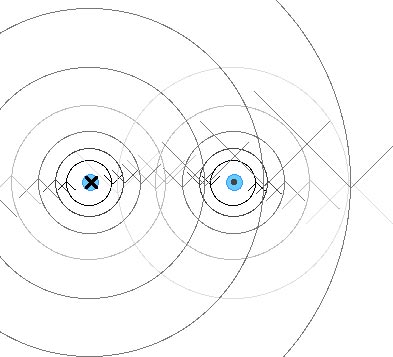
Q3 Two parallel wires carry currents in opposite directions. Describe the nature of the resultant magnetic field created by the two wires at points

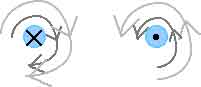
(a) between the wires and

or
Between the wires, the magnetic fields from the two wires point in the same direction so the resulting or total magnetic field will be large.
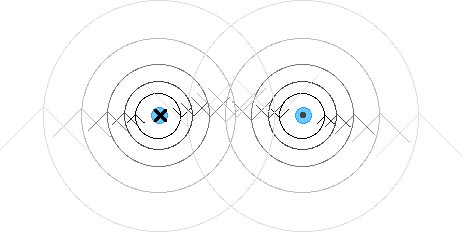
(b) outside the wires in a plane containing them.
or
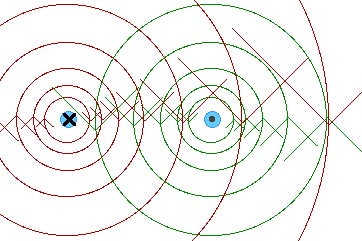
Outside the wires, the two magnetic fields from the two currents are in opposite directions so they will tend to cancel each other and the resulting or total magnetic field will be small.
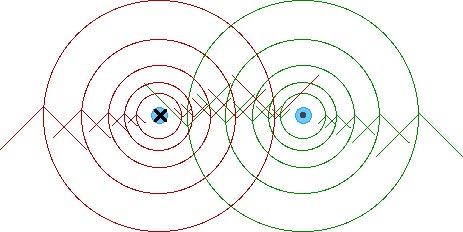
Q4 Explain why two parallel wires carrying currents in opposite directions repel each other.
You may want to look at the diagrams for Question 3. In particular, consider this diagram,

or
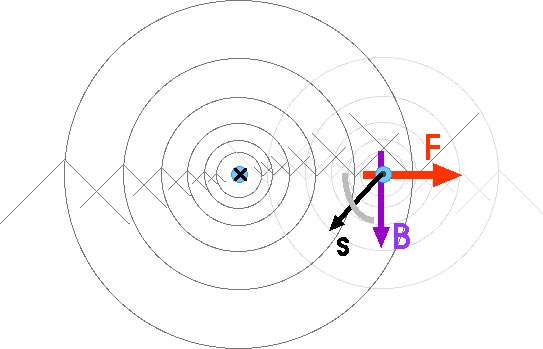
The magnetic field of the left-hand current causes a force on the right-hand current that is a repulsion so we know -- from Newton's Third Law -- that the two currents repel each other.
Q9 Describe the similarities between Ampere's law in magnetism and Gauss's law in electrostatics.
Both associate an integral around a closed surface or line with something that goes through the surface or line of the integral. Gauss's Law says the electric flux through a closed surface is proportional to the charge within that surface.. Ampere's Law says the line integral of B-ds around a closed path is proportional to the current that passes through that path.
Q18 Will a nail be attracted to either pole of a magnet? Explain what is happening inside the nail when placed near a magnet.
Yes, a nail will be attracted to either pole of a magnet. The magnet causes the boundaries between magnetic domains to move slightly, giving a net magnetic field to the nail.path If the nail is near the othermagnetic pole then different magnetic domain boundaries move.
Q19 The north-seeking ppole of a magnet is attracted toward the geographic North Pole of Earth. Yet, like poles reple. What is going on here?
The magnetic pole near Earth's geographic North Pole is what would otherwise be called a south-seeking magnetic pole.
30.8A, A conductor consists of a circular loop of radius R and two straight, long sections, as in Figure P30.8. The wire lies in the plane of the paper and carries a current I. Determine the magnitude and direction of the magnetic field at the center of the loop.
We know how to handle the magnetic field due to a straight wire;
At a distance R from the wire, the magnetic field is
And we know how to handle the magnetic field at the center of a circular loop;
At the center of the wire, the magnetic field is
So our total magnetic field at the center of the circular loop and distance R from the long, straight wire, is the sum of these,
30.22, A closely wound, long solenoid of overall length 30.0 cm (0.30 m) has a magnetic field of 4.00 x 10 - 4 T at its center produced by a current of 1.00 A through its windings. How many turns of wire are on the solenoid?
The magnetic field inside a solenoid is given by
or
n = B / I
n = (4 x 10 - 4) / [(4
x 10 - 7)(1)]
n = 318 turns/m
n = N/L
N = n L
N = (318 turns/m)(0.30 m)
N = 95 turns
30.23, A superconducting solenoid is to generate a magnetic field of 10.0 T.
(a) If the solenoid windings has 2000 turns/m, what is the required current?
or
I = B / n
I = (10)/[(4
x 10 - 7)(2000)]
I = 3979 A
That is an enormous current; but then that is an enormous magnetic field!
30.25, Some superconducting alloys at very low temperatres can carry very high currents. For example Nb3Sn wire at 10 K can carry 1000 A and maintain its superconductivity. Determine the maximum value of B achievable in a solenoid of length 25 cm (0.25 m) if 1000 turns of Nb3Sn wire are wrapped on the outside surface.
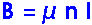
B = (4
x 10 - 7)(1000/0.25)(1000)
B = 5 T
30.32, In Figure P30.32, both currents are in the negative x direction.
(a) Sketch the magnetic field pattern in the yz-plane.
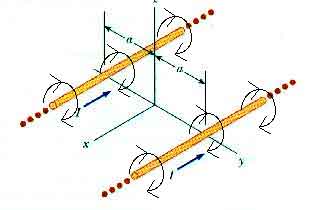

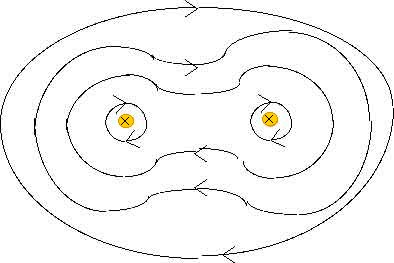
Remember, this is a rough sketch!
30.40, Consider the hemispherical closed surface in Figure P30.40. If the hemisphere is in a uniform magnetic field that makes and angle theta with the vertical, calculate the magnetic flux through
(a) the flat surface S1 and
= A B cos

A =
R2
=
R2 B cos
(b) the hemispherical surface S2.
According to Gauss's Law for magnetic flux, the total magnetic flux is zero. Since we know the flux coming into the surface (
=
R2 B cos
) that (or the negative) of that is also the flux coming out of the surface -- the flux through S2,
= -
R2 B cos
30.60, A lightning bolt may carry a current of 10,000 A for a short period of time. What is the resulting magnetic field 100 m from the botl?
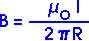
B = [(4
x 10 - 7)(10 000)]/[(2
) (100)]
B = 2 x 10 - 5 T
30.64 Two parallel conductors carry current in opposite directions as showin in Figure P30.64. One conductor carries a current of 10A. Point A is at the midpoint between the wires and point C is a distance d/2 to the right of the 10 A current. If d = 18 cm = 0.18 m and I is adusted so that the magnetic field at C is zero, find
(a) the value of the current I and
(b) the value of the magnetic field at A.
For Point C,
Bright = [(4 x 10 - 7)(10)]/[(2
)(0.09)] = 2.22 x 10 - 5 T
Bleft = [(4
x 10 - 7)( I )]/[(2
)(0.27)] = 2.22 x 10 - 5 T
I = (2.22 x 10 - 5) (0.27) / 2 x 10 - 7
I = 30 A
For Point A,
Bright = [(4 x 10 - 7)(10)]/[(2
)(0.09)] = 2.22 x 10 - 5 T
Bleft = [(4
x 10 - 7 )( 30 )]/[(2
)(0.09)] = 6.66 x 10 - 5 T
Using the Right Hand Rule, we see that these two fields point in the same direction -- "up" or "out of the page" at point A
Btotal = Bright + Bleft = 8.88 x 10 - 5 T (c) Doug Davis, 2002; all rights reserved
Return to ToC