Magnetic Fields
Homework Solutions Chapter 29, Magnetic Fields
Questions 1, 2, 3, 4, 5, 18, 21
Problems 2, 8, 11, 12, 13, 20, 28, 31
Q1 At a given instant, a proton moves in the positive x cirection in a region where there is a magnetic field in the negative z direction. What is the direction of the magnetic force? Does the proton continue to move in the positive x direction?
The vector v x B points along the positive y-direction. For a proton, q is positive, so the Force vector F = q v x B also points along the positive y-direction. With a force on it in the positive y-direction, the proton will be moved from its initial path. The proton will move in a circle in a plane parallel to the xy-plane.
Q2 Two charged particles are projected into a region where there is a magnetic field perpendicular to their velocities. If the charges are deflected in opposite directions, what can you say about them?The two particles have different or opposite charges.
Q3 If a charged particle moves in a straight line through some region of space, can you say that the magnetic field in that region is zero?
If the charged particle is moving along the magnetic field -- parallel or antiparallel to the magnetic field -- then there would be no force on it.
Q4 Suppose an electron is chasing a proton up this page when suddenly a magnetic field is formed perpendicular to the page. What happens to the particles?
They each experience a force of e v B. The force on the electron and the proton will be in opposite directions. Each will move in a circle in the plane of the page -- but in opposite directions.
Q5 Why does the picture on a TV screen become distored when a magnet is brought near the screen?
The TV's picture is created by a stream of electrons inside the picture tube. Bringing a magnet nearby causes forces on these electrons so their paths are altered and this changes or distorts the picture.
Q18 The bubble chamber is a device used for observing tracks of particles that pass through the chamber, which is immersed in a magnetic field. If some of the tracks are spirals and others are straight lines, what can you say about the particles?
The particles that leave the straight lines are uncharged particles.
Back in Question 3 we said that such straight lines could be due to moving along the direction of the magnetic field. Of course, that could also be the case here. But the researchers using the bubble chamber will be aware of that and will be careful to have the magnetic field in some other direction -- probably perpendicular to the initial direction of the particles for maximum effect.
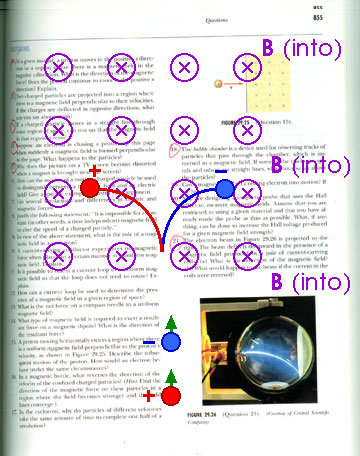
Q21 The electron beam if Figure 29.26 is projected to the right. The beam deflects downward in the presence of a magnetic field produced by a pair of current-carrying coils.
(a) What is the direction of the magnetic field?
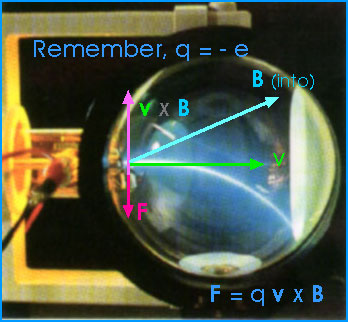
The magnetic field points into the picture. The vector v x B points up. When that is multiplied by the negative charge of the electron, the force vector F points down.
(b) What would happen to the beam if the current in the coils were reversed?As we will learn in the next chapter, if we reverese the current in the coils we will also reverse the direction of the magnetic field. That reverses the direction of all the vectors that depend upon the magnetic field. Now the force is up so the electron beam will be deflected upwards.
29.2 An electron moving along the positive x axis perpendicular to a magnetic field experiences a magnetic deflection in the negative y direction. What is the direction of the magnetic field?
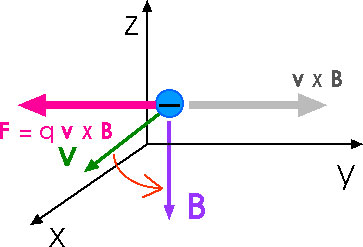
From the sketch, the magnetic field must be in the negative z-direction.
29.8 An electron is projected into a uniform magnetic field B = (1.4 i + 2.1 j) T. Find the vector expression for the force on the electron when its velocity is v = 3.7 x 105 j m/s.F = q v x B
v x B = [3.7 x 105 j] x [1.4 i + 2.1 j]
v x B = [(3.7 x 105)(1.4) (j x i)] + [(3.7 x 105)(2.1)(j x j)]
j x i = - k
j x j = 0
v x B = (3.7 x 105)(1.4) ( - k)
F = q v x B = ( - 1.6 x 10 - 19) (3.7 x 105)(1.4) ( - k)
F = ( 1.6 x 10 - 19) (3.7 x 105)(1.4) (k)
F = 8.29 x 10 - 14 N k
29.11 Show that the work done by the magnetic force on a charged particle moving in a magnetic field is zero for any displacement of the particle.
Since the force is always perpendicular to the velocity, the magnitude of the velocity (the speed) does not change. This means the Kinetic Energy does not change and that means the work is zero.
Or we could say that since the force is perpendicular to the velocity and the direction of the displacement so that means the work is zero.
29.12 A wire 40 cm long carries a current of 20 A. It is bent into a loop and placed with its plane perpendicular to a magnetic field having a flux density of 0.52 T. What is the torque on the loop if it is bent into
The torque on a current loop depends upon the area of the current loop. When the magnetic field is perpendicular to the plane of the loop the torque has its maximum value,
= I A B
We know I and B for all these cases but A depends upon the geometry
(a) an equilateral triangle,
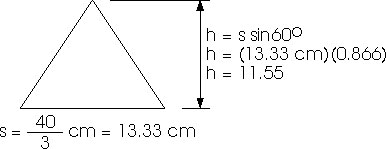
A = (1/2) s h
A = (1/2) (13.33 cm)(11.55 cm)
A = 76.98 cm2
(b) a square,
The 40 cm of wire can be bent into a square with sides of 10 cm;
A = (10 cm)2 = 100 cm2
(c) a circle.
The 40 cm of wire can become a circumference for a circle. We need the radius of that circle;
C = 2
r
40 cm = 2
r = 40 cm/(2
r = 6.37 cm
A =
A = (
A = 127.5 cm2
(d) Which torque is greatest?
The circle has the greatest area so it should provide the greatest torque.
29.13 A wire carries a steady current of 2.4 A. A straight section of the wire is 0.75 m long and lies along the x axis within a uniform magnetic field, B = (1.6 k) T. If the current is in the + x direction, what is the magnetic force on that section of wire?
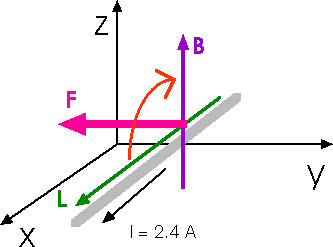
F = I L x B
F = I L B
F = (2.4 A)(0.75 m)(1.6 T)
F = 2.88 N
From the diagram, we find that this force acts in the negative y-direction
F = - 2.88 N j 29.20 A rod of mass 0.72 kg and radius 6.0 cm rests on two parallel rails (Fig P29.20) that are d = 12 cm apart and L = 45 cm long. The rod carries a current I = 48 A in the direction shown and rolls along the rails without friction. If the rod starts from rest, what is its speed as it leaves the rails if there is a uniform 0.24-T magnetic field directed perpendicular to the rod and the rails?
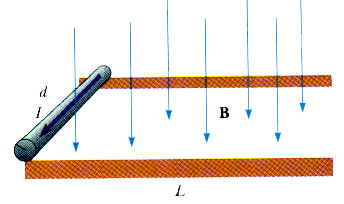
F = I L B
Be careful. This equation uses "L" for the length of the conductor in the magnetic field; and that is just 12 cm or L = 0.12 m. However, this question uses "L" to mean a distance of 45 cm that the rod moves while in contact with the current-carrying rails. I am going to change that to s = 0.45 m
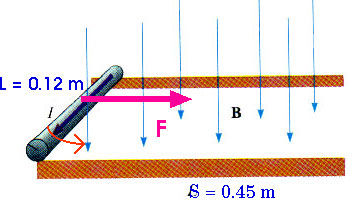
F = (48 A)(0.12 m)(0.24 T) = 1.38 N
F = ma
a = F/m
a = 1.38 N / 0.72 kg = 1.92 m/s2
v2 = vo2 + 2 a S
v2 = 02 + 2 (1.92 m/s2) (0.45 m)
v2 = 1.73 m2/s2
v = 1.31 m/s
Hmmmm, . . . That's not quite right. That is the final velocity if the rod slides with no friction. We could also have gotten that result by setting the work equal to the kinetic energy.
W = F S = (1.38 N)(0.45 m) = 0.621 N-m = 0.621 J KE = (1/2) m v2 = (1/2)(0.72 kg) v2
(1/2)(0.72 kg) v2 = 0.621 J
v2 = 1.73 m2/s2
v = 1.31 m/s
But this rod has a radius of 6 cm (0.06 m) so its rotational kinetic energy is going to be important.
KErot = (1/2) I 2
where I is now the moment of intertia (the "rotational mass") rather than the current!
I = (1/2) m r2 I = (1/2) (0.72 kg) (0.06 m)2
I = 0.0013 kg-m2
KErot = (1/2) I
KEtot = KEtran + KErot
KEtot = (1/2) m v2 + (1/2)(I/r2) v2
KEtot = (1/2)[m + I/r2 ] v2
I/r2 = [(1/2) m r2 ]/r2 = (1/2) m
KEtot = (1/2)[m + (1/2) m ] v2
KEtot = (1/2) [(3/2) m] v2
KEtot = (3/4) m v2 = (3/4)(0.72 kg) v2 = (0.54 kg) v2
(0.54 kg) v2 = 0.621 J = Work
v2 = 0.621 J / 0.54 kg
v2 = 1.15 m2/s2
v = 1.07 m/s
This is considerably different from the value of v = 1.31 m/s we got when we ignored the rotation. So the rotational effects are important for this situation.
29.28 The magnetic field of the Earth at a certain location is directed vertically downward and has a magnitude of 0.5 x 10 - 4 T. A proton is moving horizontally towards the west in this field with a speed of 6.2 x 106 m/s.
(a) What are the direction and magnitude of the magnetic force the field exerts on this charge?
From the diagram we see that the force is directed to the South. Since v and B are perpendicular, the magnitude of the force is
F = q v B
F = (1.6 x 10 - 19 C)(6.2 x 106 m/s)(0.5 x 10 - 4 T)
F = 4.96 x 10 - 19 T
(b) What is the radius of the circular arc followed by this proton?
This force supplies the centripetal force,
Fc = m v2/r = Fmag
r = m v2/Fmag
r = [(1.67 x 10 - 27)(6.2 x 106)2/4.96 x 10 - 19] m
r = 1.29 x 105 m
r = 129 km
As magnetic fields go, Earth's magnetic field is not esp'ly strong. But it does rotate magnets!
29.31 A proton moving in a circular path perpendicular to a constant magnetic field takes 1.00 microseconds to complete one revolution. Determine the magnitude of the field.Fc = m v2/r = q v B = Fmag
m v/r = q B
B = m v / r q
How is the period related to velocity and radius?
v = C/T = 2 pi r/T T = 2 pi r/v
v/r = 2 pi/T
B = m v / r q
B = (1.67 x 10 - 27 kg)[2 pi/(1 x 10 - 6 s)]/(1.6 x 10 - 19 C)
B = 2 pi (1.67 x 10 - 27 kg)/[(1 x 10 - 6 s)(1.6 x 10 - 19 C)]
B = 0.0656 T
(c) Doug Davis, 2002; all rights reserved
Return to ToC
