

Current and Resistance
Homework Solutions Questions 2, 3, 4, 5, 7, 9, 17, 20
Problems 1, 2, 7, 8, 15, 16, 22, 27, 33, 36, 43, 45, 46, 48, 49, 52
Q2 What factors affect the resistance of a conductor?
Length, cross-section, material, and temperature all affect the resistance.Q3 What is the difference between resistance and resistivity?
Resistance is the value of the ratio of voltage across a resistance divided by the current through the resistor. Resistivity is a characteristic of the material of which a resistor is made.Q4 Two wires, A and B, of circular cross-section are made of the same metal and have equal lengths, but the reistance of wire A is three times greater that that of wire B. What is the ratio of their cross-sectional areas? How do their radii compair?
Recall our equationR = L / A
Being made of the same material means the resistivity
is the same for the two wires. They have the same lengths. Their cross sectional areas A must differ by a factor of 3. Since
A = r2
the radii must vary as the square root of 3.
Q5 What is required in order to maintain a steady current in a conductor?
A steady potential difference (or voltage). This also means a steady electric field within the conductor -- caused by the steady voltage.Q7 When the voltage across a certain conductor is doubled, the current is observed to increase by a factor of three. What can you conclude about the conductor?
This conductor does not follow Ohm's Law.Q9 Why might a "good" electrical conductor also be a "good" thermal conductor?
Electrons, free to move about a material -- such as a metal -- conduct electricity and they also conduct heat.Q17 Two conductors of the same length and radius are connected across the same potential difference. One conductor has twice the resistance of the other. Which conductor will dissipate more power?
P = I V = I2 R = V2/R Use
P = V2/R The voltage is the same for both, of course. The one with the smaller resistance will dissipate the greater power.
Q20 Two lightbulbs both operate from 110 V, but one has a power rating of 25 W and the other, of 100 W. Which bulb carries the greater current?
P = I V = I2 R = V2/R Use
P = I V or
I = P / V For the same voltage (110 V), the current is proportional to the power. So the 100 W bulb carries four times the current of the 25 W bulb.
27.1 In the Bohr model of the hydrogen atom, an electron in the lowest energy state follows a circular path, 5.29 x 10 - 11 m from the proton.
(a) Show that the speed of the electron is 2.19 x 106 m/s.
What holds the electron in its orbit? The centripetal force is supplied by the electric force from Coulomb's LawFc = m v2/r = k Qq/r2 = Fel m v2/r = k e2/r2
v2 = k e2/r m
v2 = (9x109)(1.6x10-19)2/[(5.29x10-11)(9.11x10-31)]
v2 = 4.78 x 1012 m2/s2
v = 2.19 x 106 m/s
(b) What is the effective current associated with this orbiting electron?
Current is given byI = dQ/dt What is the period of this electron in orbit?
v = C/T T = C/v
T = 2
r / v
T = 2
(5.29x10-11) / (2.19 x 106 m/s)
T = 1.52 x 10 - 16 s
That is, an electron, with Q = e = 1.6 x 10 - 19 C of charge passes by every 1.2 x 10 - 16 s for a current of
I = 1.6 x 10 - 19 C/1.52 x 10 - 16 s I = 1.05 x 10 - 3 A
I = 1.05 mA
27.2 In a particular cathode ray tube, the measured beam current is 30
A. How many electrons strike the tube screen every 40 s?
I = Q/
t
Q = N e
I = N e / 40 s
N = (40 s)(I)/e
N = (40 s)(30 x 10 - 6 C/s)/1.6 x 10 - 19 C
N = 7.5 x 1015
27.7 A Van de Graaff generator produces a beam of 2.0-MeV deuterons which are heavy hydrogen nuclei containing a proton and a neutron.
(a) If the beam current is 10.0
A, how far apart are the deuterons in the beam?
First, what is the speed of the deuterons?E = KE = (1/2) m v2 = 2.0 MeV[106 eV/MeV][ 1.6 x 10 - 19 J / eV] Recalling that
eV = (1.6 x 10 - 19 C)(V)[(J/C)/V] = 1.6 x 10 - 19 J (1/2) m v2 = 3.2 x 10 - 13 J
What is the mass of a deuteron? From Table A.3, page A.4, we find
m = 2.014 u measured in u, "unified mass units". But what's a u?
1 u = 1.66 x 10 - 27 kg m = 2.014 u [1.66 x 10 - 27 kg/u]
m = 3.34 x 10 - 27 kg
(1/2))(3.34 x 10 - 27 kg) v2 = 3.2 x 10 - 13 J
v2 = 2(3.2 x 10 - 13 J)/3.34 x 10 - 27 kg
v2 = 1.92 x 1014 m2/s2
v =1.38 x 107 m/s
I =
Q/
t
Call the time between deuterons T. Each deuteron has a charge of e.
I = e / T T = e / I
T = (1.6 x 10 - 19 C) / ( 10 x 10 - 6 C/s)
T = 1.6 x 10 - 14 s
How far does a deuteron travel in this time?
v = L/T L = v T = (1.38 x 107 m/s)(1.6 x 10 - 14 s)
L = 2.21 x 10 - 7 m
That's the distance between deuterons in the beam.
(b) Is their electrostatic repulision a factor in beam stability?
With distances like 10 - 7 m, the electrostatic force between two deuterons will be very large and, therefore, will certainly effect the beam stabilityFel = k Qq/r2 Fel = k e2/r2
Fel = (9x109)(1.6x10 - 19)2/(2.21x10 -7)2
Fel = 4.72 x 10 - 15 N
While that seems like a small number, let's apply Newton's Second LAW (F=ma) and see what sort of acceleration that would produce on a deuteron,
F = m a a = F/m
a = 4.72 x 10 - 15 N / 3.34 x 10 - 27 kg
a = 1.41 x 1012 m/s2
27.8 Calculate the average drift speed of electrons traveling through a copper wire with a cross-sectional area of 1.00 mm2 when carrying a current of 1.0 A (values similar to those four the electric wire to your desk lamp). It is known that about one electron per atom of copper contributes to the current. The atomic weight of copper is 63.54 and its density is 8.92 g/cm3.
From Equation 27.4, we havevd = I / n q A vd = 1.0 A / [n (1.6 x 10 - 19 C) (1.0 mm2)]
(As always) be careful of the units! It is easier to state the cross-sectional area as A = 1.0 mm2 but we need that in m2 by the time we carry out the calculation.
A = 1.0 mm2 [1 m/1000 mm]2 A = 1.0 x 10 - 6 m2
Be careful. While 1000 mm = 1 m, we need a conversion that involves millimeters-squared, 106 mm2 = 1 m2
vd = 1.0 A / [ n (1.6 x 10 - 19 C) (1.0 - 6 m2) ] Now, what about n, the "number density" of the electrons in the copper wire?
n = NA/vmol vmol = Mmol/density
vmol = 63.54 g/[8.92 g/cm3]
That is, the volume of one mole of copper is
vmol = 7.12 cm3 Again, while it is easier to think of 7.12 cm3, we need to convert this to cubic meters before we plug it into an equation,
vmol = 7.12 cm3 [ m / 100 cm ]3 vmol = 7.12 x 10 - 6 m3
n = NA/vmol
n = (6.02 x 1023)/(7.12 x 10 - 6 m3)
n = 8.46 x 1028 (1/m3)
or
n = 8.46 x 1028 electrons/m3 vd = 1.0 A / [n (1.6 x 10 - 19 C) (1.0 - 6 m2)]
vd = 1.0 A / [(8.46 x 1028 (1/m3)) (1.6 x 10 - 19 C) (1.0 - 6 m2)]
vd = 7.39 x 10 - 5 m/s
27.15 Calculate the resistance at 20oC of a 40-m, length of silver wire having a cross-sectional area of 0.40 mm2.
R = L /A
A = 0.4 mm2 [ 1 m / 1000 mm ]2 = 4 x 10 - 7 m2
R = (1.59 x 10 - 8
-m)(40 m)/(4 x 10 - 7 m2)
R = 1.59

27.16 Eighteen-gauge wire has a diameter of 1.024 mm. Calculate the resistance of 15.0 m of 18-gauge copper wire at 20.0oC.
R = L /A
A =
r2
r = 1.024 mm / 2 = 0.512 mm = 5.12 x 10 - 4 m
A =
(5.12 x 10 - 4 m)2 = 8.235 x 10 - 7 m2
R =
L /A
R = (1.7 x 10 - 8
-m)(15 m)/(8.235 x 10 - 7 m2)
R = 0.31

27.27 A resistor is constructed of a carbon rod that has a uniform cross-sectional area of 5.0 mm2. When a potential difference of 15 V is applied across the ends of the rod, there is a current of 4.0 x 10 - 3 A in the rod.
Find (a) the resistance of the rod and (b) the length of the rod.
R = V/I R = 15 V / 4.0 x 10 - 3 A
R = 3,750

A = 5.0 mm2 [ 1 m / 1000 mm ]2 = 5 x 10 - 6 m2
R =
L /A
L = R A /
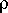
L = (3,750
)(5 x 10 - 6 m2) / (3.5 x 10 - 5
-m)
L = 535.7 m
That seems unreasonable!
27.33 If a copper wire has a resistance of 18 ohms at 20oC, what resistance will it have at 60oC?
R(T) = Ro [ 1 + 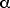
T ]R(60oC) = (18
) [ 1 + (3.9 x 10 - 3 (1/Co))(40 Co)]R(60oC) = (18
) [ 1 + 0.156]R(60oC) = (18
) [ 1.156 ]R(60oC) = 20.8
27.36 A segment of Nichrome wire is initially at 20oC. Using the data from Table 27.1, calculate the temperature to which the wire must be heated to double its resistance.
R(T) = Ro [ 1 + 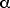
T ]
R(T) = 2 Ro
2 Ro = Ro [ 1 +
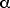
T ]
2 = [ 1 +
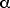
T ]
1 =
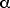
T
T = 1/
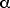
T = 1/[3.9 x 10 - 3 (1/Co)]
T = 256 Co
Tf = 276oC
27.43 A 10-V battery is connected to a 120-![]() resistor. Neglecting the internal resistance of the battery,
calculate the power dissipated in the resistor.
resistor. Neglecting the internal resistance of the battery,
calculate the power dissipated in the resistor.
P = I V = I2 R = V2/R P = V2/R
P = (10 V)2/120

P = 0.833 W
27.45 Suppose that a voltage surge produces 140 V for a moment. By what percentage will the output of a 120-V, 100-W lightbulb increase, assuming its resistance does not change?
P = I V = I2 R = V2/R P = V2/R
Po = (120 V)2/R
Pnew = (140 V)2/R Pnew/Po = 1402/1202
Pnew/Po = 1.36
That is, the power increases by 36%
27.46 A particular type of automobile storage battery is characterized as "360-ampere-hours, 12 V". What total energy can the battery deliver?
E = P T P = I V = I2 R = V2/R
P = I V
E = (360 A-h)(12 V) [ 3600 s/h ]
E = 1.56 x 107 J
27.48 In a hydroelectric installation, a turbine delivers 1500 hp to a generator whichin turn converts 80% of thae mechanical energy into electrical energy. Under these conditions, what current will the generator deliver at a terminal potential difference of 2000 V?
1 hp = 0.746 kW = 746 W Pout = (1500 hp) [ 746 W/hp ] (0.80)
Pout = 8.95 x 105 W
P = I V
I = P/V
I = 8.95 x 105 W / 2000 V
I = 448 A
27.52 The heating element of a coffee maker operates at 120 V and carries a current of 2.0 A. Assuming that all of the heat generated is absorbed by the water, how long does it take to heat 0.50 kg of water from room temperature of 23oC to the boiling point.
Q = C m
T
Q = (4186 J/kg-Co)(0.50 kg)(77 Co)
E =
Q = 1.61 x 106 J
E = P
t
t = E/P
P = I V = (2.0 A)(120 V) = 240 W
t = (1.61 x 106 J)/240 W
t = 672 (J/W)[(W-s)/J]
t = 672 s [min/60 s]
t = 11.2 min
|
|
|
|
|
|
|
|
Ch 28 DC Circuits |
|
|
|
|||