

Capacitors
Homework Solutions
Questions: 2, 4, 11, 14, 17
Problems: 5, 12, 13, 27, 29, 30, 38, 47, 92
Q2. The plates of a capacitor are connected to a battery. What happens to the charge on the plates if the connecting wires are removed from the battery? What happens to the charge if the wires are removed from the battery and connected to each other?
If the wires to the battery are disconnected, the charge remains on the plates -- and the voltage across the plates remains the same. If the wires are connected to each other, current will flow and the capacitor will discharge. Then there will be no voltage across the capacitor nor any charge on the plates.
Q4. A pair of capacitors are connected in parallel while an identical pair are connected in series. Which pair would be more dangerous to handle after being connected to the same voltage source?
Each pair will carry the same voltage. The ones in parallel will carry a greater charge and, therefore, could do more "damage" as they discharge.
Q11. If the potential difference across a capacitor is doubled, by what factor does the energy stored change?
PE = U = (1/2) C (
V)2 means that if
V is doubled then (
V)2 will be increased by a factor of four so the potential energy is increased by four.
Q14. An air-filled capacitor is charged, then disconnected from the power supply, and finally connected to a voltmeter. Explain how and why the voltage reading changes when a dielectric is inserted between the plates of the capacitor.
The charge will remain the same. The electric field very close to the capacitor plate will remain the same. But the electric field throughout the dielectric is reduced. Remember that E = -
V/
x or
V = E
x so if the electric field is reduced the voltage, too, will be reduced.
The corollary to this is, if the voltage is kept constant -- by connecting it to a battery -- then the charge stored on the capacitor will be increased. That's what we usually think of. Inserting a dielectric into a capacitor increases the charge it can store for a given voltage. That is, inserting a dielectric increases the capacitance.
Some useful prefixes:
m = milli- = 10 - 3
= micro- = 10 - 6
n = nano- = 10 - 9
p = pico- = 10 - 12
26.5. A parallel-plate capacitor has a capacitance of 19.0 microFarads (19.0
F = 19.0 x 10 - 6 F) What charge on each plate produces a potential difference of 36.0 V between the plates?
C = Q/V Q = C V
Q = (19.0 x 10 - 6 F)(36.0 V)
Q = 6.84 x 10 - 4 C
26.12. The plates of a parallel-plate capacitor are separated by 0.20 mm. If the space betweenthe plates is air, what plate area is required to provide a capacitance of 9.0 pF (picoFarads = 10 - 12 F)?
C = A / d
A = C d /

A = (9.0 x 10 - 12 )(0.000 2) / (8.85 x 10 - 12 )
2.034 x 10 - 4 m2
26.13. When a potential difference of 150 V is applied to the plates of a parallel-plate capacitor, the plates carry a surface charge density of 30 nC/cm2 (nC = nanoCoulombs = 10 - 9 C). What is the spacing between the plates?
C = Q / V C = (
A) / V
C/A =
/ V
C =
A / d
C / A =
/ d
/ V =
/ d
d = V
/

= [ 30 x 10 - 9 C/cm2 ][104 cm2/m2] = 3.0 x 10 - 4 C/m2
d = (150 V)(8.85 x 10 - 12 )/(3.0 x 10 - 4 C/m2)
d = 4.4 x 10 - 6 m
d = 4.4 x 10 - 3 mm
Units are important! We can carry them through -- and I have often done that and it is useful and worthwhile to do that -- or we can make sure we have everything in "standard units" -- meaning distances in meters!
26.27. (a) Two capacitors, C1 = 2.0 microFarads = 2.0
F and C2 = 16.0 microFarads = 16.0
F, are connected in parallel. What is the equivalent capacitance of the combination?
For capacitors in parallel, we have
Ceq = C1 + C2 Ceq = 2.0
F + 16.0
F
Ceq = 18.0
F
(b) Calculate the equivalent capacitance of the two capacitors if they are connected in series.
For capacitors in series, we have
1/Ceq = 1/C1 + 1/C2 [[
Caution: Remember 1/3 + 1/2 =/= 1/5 !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
It is almost always better to do these as decimals rather than to try to "do them in your head".
]]
1/Ceq = 1/C1 + 1/C2
1/Ceq = 1/2.0
F + 1/16.0
F
[[
The correct answer is not 18
F and the correct answer is not ( 1/18 )
F .
]]
1/Ceq = 0.5/ F + 0.0625/
F
1/Ceq = ( 0.5 + 0.0625 ) /
F
1/Ceq = 0.5625 /
F
Ceq = (1/0.5625)
F
Ceq = 1.778
F
26.29. (a) Determine the equivalent capacitance for the capacitor network shown in Figure P26.29.
First, replace the 3.0
F and 6.0
F capacitors with a single capacitor that is equivalent to the two of them, connected in series,
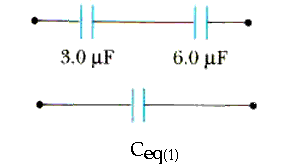
1/Ceq1 = 1/3.0
F + 1/6.0
F
1/Ceq1 = 0.3333 /
F + 0.1667 /
F
1/Ceq1 = (0.3333 + 0.1667) /
F
1/Ceq1 = (0.500) /
F
Ceq1 = (1/0.500)
F
Ceq1 = 2.0
F
Now replace the two capacitors in parallel with a single equivalent capacitor;
Because of the particular choice of numbers, there is some unexpected symmetry in this problem.
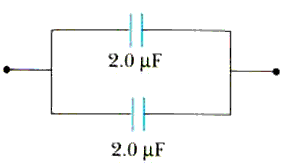
For two capacitors in parallel, the equivalent capacitance is given by
Ceq2 = C1 + C2 Ceq2 = 2.0
F + 2.0
F
Ceq2 = 4.0
F
(b) If the network is connected to a 12-V battery, calculate the potential difference across each capacitor and the charge on each capacitor.
Now we work backward until we have all the information about all of the capacitors.
For this final equivalent capacitor with capacitance Ceq2, the voltage across it is, of course, 12.0 V. The charge on this capacitor, Qeq2, is
C = Q / V Q = C V
Qeq2 = (4.0 x 10 - 6 F) (12 V) = 4.8 x 10 - 5 C
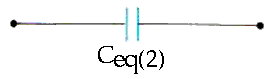
That same voltage, 12 V, is the voltage (or potential difference) across the real 2.0
F capacitor and the earlier equivalent capacitance Ceq1. Let's look at the 2.0
F capacitor first.
V2 = 12 V Q = C V
Q2 = (2.0 x 10 - 6 F)(12 V) = 2.4 x 10 - 5 C
Now we will investigate this earlier equivalent capacitor Ceq1 more closely;
This equivalent capacitor Ceq1 has the same charge as the 3.0
F capacitor and the 6.0
F capacitor. That is,
Q3 = Q6 = Qeq1 = Ceq1 Veq1 Veq1 = 12 V
Q3 = Q6 = Qeq1 = Ceq1 Veq1 = (2.0 x 10 - 6 F)(12 V)
Q3 = Q6 = Qeq1 = 2.4 x 10 - 5 C
Now we know all the charges and we can go back and find the voltages;
C = Q/V V = Q / C
V3 = Q3/C3 = 2.4 x 10 - 5 C/3.0 x 10 - 6 F = 8 V
V6 = Q6/C6 = 2.4 x 10 - 5 C/6.0 x 10 - 6 F = 4 V
Notice, of course, that
V3 + V6 = 8 V + 4 V = 12 V as it must.
26.30. Evaluate the equivalent capacitance of the configuration shown in Figure P26.30. All the capacitors are identical, each with a capacitance C.
Replace each "bank" of capacitors in series with an equivalent capacitor;
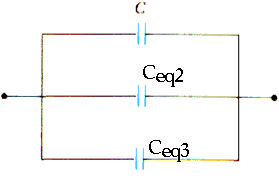
Ceq2 is the equivalent capacitance of the two C's in series so that value comes from
1/Ceq2 = 1/C + 1/C
1/Ceq2 = 2/C
Ceq2 = C/2
Likewise, Ceq3 is the equivalent capacitance of the three C's in series so that value comes from
1/Ceq3 = 1/C + 1/C + 1/C
1/Ceq3 = 3/C
Ceq3 = C/3
Now find the "final equivalent capacitor" with value of CEq that is equivalent to these three capacitors in parallel;
CEq = C + Ceq2 + Ceq3
CEq = C + C/2 + C/3
CEq = C [ 1 + 1/2 + 1/3 ]
CEq = C [ 11/6 ]
CEq = (11/6) C
CEq = (11/6) C
26.38. Find the equivalent capacitance between points a and b for the group of capacitors connected as shown in Figure P26.38 if C1 = 5.0
F and C2 = 10.0
F and C3 = 2.00
F.
Can you immediately see that capacitors C1 and C2 are in series in the upper part of the schematic. They are. But it is often worthwhile to redraw a circuit and see how it looks if it is simply rewrawn;
For both of those pioeces, we can replace them by an equivalent capacitor Ceq1; since they are in series, this has a value of
1/Ceq1 = 1/C1 + 1/C2 1/Ceq1 = 1/(5.0
F) + 1/(10.0
F)
1/Ceq1 = (0.20 + 0.10)/
F
1/Ceq1 = 0.30/
F
Ceq1 = (1/0.30)
F
Ceq1 = 3.33
F
Now, redraw the diagram again;
Now, those three in parallel can be replaced with a single equivalent capacitor,
Ceq2 = 3.33 F + 2.0
F + 3.33
F
Ceq2 = 8.66
F
Now our circuit or network looks like this --
We must replace the two C2's that are in parallel with another equivalent capacitor, Ceq3;
Ceq3 = C2 + C2 Ceq3 = 10.0
F + 10.0
F
Ceq3 = 20.0
F
Now or circuit or network is two capacitors in series;

1/CEq = 1/8.66
F + 1/20.0
F
1/CEq = [ 0.1155 + 0.05] [1/
F]
1/CEq = [ 0.1655 ] [1/
F]
CEq = 6.04
F
26.47. The energy stored in a 12.0
F capacitor is 130
J. Determine the following:
(a) the charge on the capacitor and
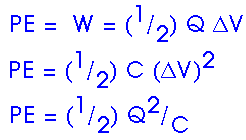
PE = U = (1/2) Q2/C
130
J = (1/2) Q2/12.0
F
130 x 10 - 6 J = (1/2) Q2/12.0 x 10 - 6 F
(130 x 10 - 6 J)(12.0 x 10 - 6 F)(2) = Q2
Q2 = 3.12 x 10 - 9 C2
Q = 5.59 x 10 - 5 C
(b) the potential difference across it.
C = Q/V V = Q/C
V = (5.59 x 10 - 5 C)/(12.0 x 10 - 6 F)
V = 4.65 V
26.92. Determine the effective capacitance of the combination shown in Figure P26.92. (Hint: Consider the symmetry involved!)
Symmetry is vital to this solution. We do not have the tools -- the theory or the equations -- to solve for a more general form of this network. We can handle only capacitors in series or in parallel. With this one in the middle -- the 3C capacitor -- this network is not a collection of pieces that are in series or in parallel. However, . . . Look at the potential difference between points c and d -- or between a and c and between a and d.
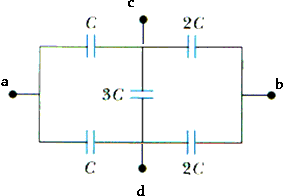
Vac = Vad
Vcb = Vdb
Vcd = 0
With zero potential difference across this 3C capacitor, it does nothing! It has no charge on it. We can pull it out entirely;
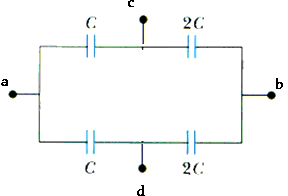
Now it's easy and straightforward to replace the two capacitors in series,
1/Ceq1 = 1/C + 1/2C 1/Ceq1 = (1.0 + 0.5)/C
1/Ceq1 = (1.5)/C
Ceq1 = 0.667 C
Now we have two capacitors in parallel and we can replace them with a final equivalent capacitor CEq
CEq = 0.667 C + 0.667 C CEq = 1.333 C

Ch 27, ToC
Return to ToC (c) Doug Davis, 2002; all rights reserved