

Electric Potential
Electric Potential due to a Point Charge Consider the electric potential due to a point charge q, As we move from point A, at distance rA from the charge q, to point B, at distance rB from the charge q, the change in electric potential is
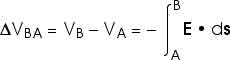
Remember, the little "caret" or "hat" over the vector r means this is a unit vector -- it points in the radial direction and has a magnitude of one.
Only the radial distance r determines the work done or the potential. We can move through any angle we like and, as long as the radial distance remains constant, no work is done or there is no change in the electric potential.

This is the change in electric potential due to a point charge as we move from rA to rB.
We could ask about the change in electric potential energy as we move a charge q' from radius rA to rB due to a point charge q,
As with gravitational potential energy, it is more convenient -- and, therefore, useful -- to talk about the electric potential energy or the electric potential relative to some reference point. We will choose that reference point to be infinity. That is,
That means we can then write the electric potential at some radius r as
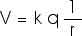
If we bring in a charge q', a distance r, from charge q, it (or "the system") will have electric potential energy of
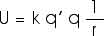
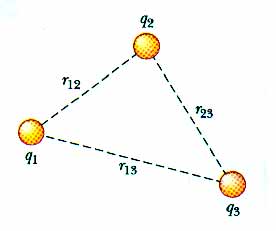
Here are charges q1 and q2, a distance r12 apart. Their electric potential energy is
That is, that much work is required to bring these two charges in from infinitly far away to this present distance of r12 apart. Think of bringing q1 in initially. With no other charges around, no work is required. Now, with q1 in place, bring in charge q2 from infinity to r12. The work required is now stored up as electric potential energy. Of course we can talk about the "point in space" located at distance r12 from charge q1 and talk about the electric potential at that point.
Remember, energy is a scalar. Electric potential is a scalar.
We have equations to tell us the electric potential energy of two charges or the electric potential at a point in space because of one electric charge. What if we have more than one electric charge?
That is, the total or net electric potential is the scalar sum of the electric potential due to each of the individual point charges qi.
There are no navigational links from these Numerical Examples to get BACK to this page. You will have to use BACK or GO from your internet browser.
(c) Doug Davis, 2002; all rights reserved
Return to Ch25 ToC